最初に、材料・製品設計と、プロセス・装置設計の話をします。

材料設計・製品設計

こちら：分子設計・化学構造設計の概要と研究の方向性 (化合物データベース利用) のような分子設計により、化合物を開発した後は、それを適切に材料や製品にしなければなりません。薬を例にすれば、分子設計で原薬を開発した後に、それを効果的に人の体に届けるための錠剤 (製品) を作る感じです。

材料に求められる物性・製品に求められる特性は、原料の化合物だけでなく、材料の作り方・製品の製造の仕方によっても変わります。胃で効く錠剤と、腸で効く錠剤とでは、作り方は違いますよね。材料や製品を、望ましい物性・特性にするためには、実験条件や製造条件を最適化する必要があるわけです。

たとえば、高分子材料 (ポリマー) を作るとき、ポリマーの強度・硬さ・密度・ガラス転移温度などのポリマー物性は、単分子 (モノマー) の種類・モノマーの組成比・反応温度・反応時間などによって変わります。望ましいポリマー物性を満たすための実験条件・製造条件を設計する必要はあるのです。そして、実験・製造コストや開発期間の観点から、なるべく少ない実験回数で、欲しい物性を得るための実験条件・製造条件を決めることが求められています。

プロセス設計・装置設計

そして実際に材料・製品を作るとき、作るためのプロセス・装置も設計しなければなりません。反応器とか蒸留塔とかそういったものの形状や大きさなどを、材料・製品の収率・生産量などがよい値になるように、そして副生成物の量が少なくなるように、設計するわけです。

たださすがに、そういった装置を実際に作ってみて実験して、材料・製品の収率・生産量を確認して、また装置を作り直して確認して、・・・といったことを繰り返すことはコスト的な観点からもできません。

そのため、コンピュータ上で仮想的な装置 (装置のモデル、数式) を作って、シミュレーションします。これなら、実際に装置を作らなくても、コンピュータ上で装置をいろいろと変えて、収率・生産量などを確認できます。

しかし、複雑な装置になればなるほど、より詳細なモデル・正確な装置モデルにすればするほど、装置モデルは複雑になり、シミュレーションにも時間がかかってしまいます。なるべく少ないシミュレーション回数で、望ましい装置を設計したいわけです。

実験計画法

材料設計・製品設計では、なるべく少ない実験・製造回数で望ましい実験条件・製造条件を決めたい、プロセス設計・装置設計ではなるべく少ないシミュレーション回数で望ましい装置パラメータを決めたい、といった話をしました。では、とりあえず最初、どのような実験条件・製造条件で実験・製造を行えばよいでしょうか？どのような装置パラメータでシミュレーションすればよいでしょうか？

１つの方法が、実験計画法です。実験計画法についてはこちらをご覧ください → 実験計画法の概要～データを上手く使って実験のコスパを上げましょう！～。

実験計画法によって選ばれた実験条件・製造条件の候補で実験したり、装置パラメータの候補でシミュレーションしたりします。

適応的な実験計画法

実験計画法で選ばれた実験条件・製造条件の候補の中で、目標の物性を達成できるものがあったり、装置パラメータの候補の中で、目標とする装置のシミュレーション結果が得られたりすればよいのですが、必ずしもそうはなりません。ではどうしましょうか。

これまでの実験結果・シミュレーション結果を活用して、次の実験候補・シミュレーション候補を決めるのです。流れは下図のようになります。

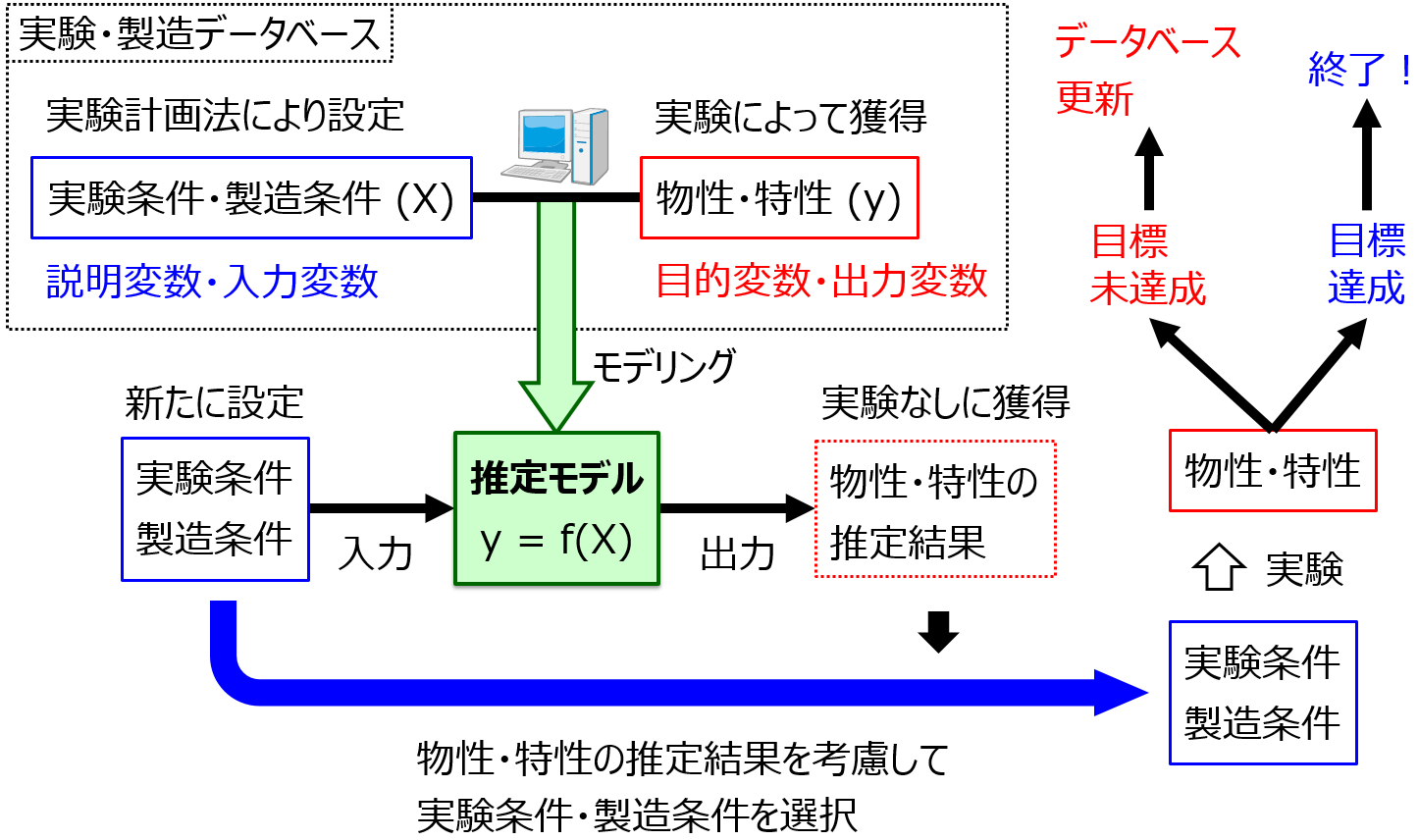
ここでは、材料設計・製品設計を対象にして、目標の物性を達成できるような実験条件・製造条件を探索することについて説明します。ただ、「実験条件・製造条件」を「装置パラメータ」、「目標の物性」を「目標の収率・生産量」、「実験」を「シミュレーション」とすれば、そのままプロセス設計・装置設計の説明になります。

まず、実験計画法によって選ばれた実験条件・製造条件の候補での実験結果がありますので、その実験データを用いて、実験条件・製造条件 X と物性・特性 y との間で回帰分析もしくはクラス分類を行います。X から y を推定するモデル (回帰モデル・クラス分類モデル) を作るわけです。

このモデルがあると、新たに設定した実験条件・製造条件をそのモデルに入力することで、実験せずに物性値を推定することができます。あたかも実験したかのように、です。そしてこの推定結果を見て、たとえば望ましい物性値になるような実験条件・製造条件はどれかな？、といった感じで検討します。このように、望ましい y の値があったときに、それを達成できる X の候補をモデルにより選ぶことを、モデルの逆解析と呼びます。

この逆解析のやり方として、新たに設定した実験条件・製造条件から、実際に実験する条件を選ぶとき、物性の推定値が目標の物性値になるべく近いものを選択する、というやり方があると思います。ただ、この方法がいつもうまくいくわけではありません。こちらに書いたようなモデルの適用領域・適用範囲を考慮していないためです。それぞれの推定値がどれくらい信用できるものなのか、考えなければいけません。

推定値だけでなく、その推定値の信頼性まで考慮して、次の実験条件の候補を選ぶやり方の１つとして、ベイズ最適化があります。ベイズ最適化では、それぞれの推定値は確率分布で与えられます。推定値が 5 になる確率は 0.2 といった具合です。その確率と、目標とする物性値に基づいて、実験条件・製造条件の候補ごとに、目標の物性を達成する確率や物性の期待値を計算します。ベイズ最適化の詳細についてはこちらをご覧ください。

ベイズ最適化によって得られた確率や物性の期待値の大きい実験条件・製造条件の候補を探すことになります。たとえば、実験条件・製造条件をランダムに振り、すべての実験条件・製造条件の候補の中から、確率や期待値の大きいものを選ぶとか、遺伝的アルゴリズムなどの最適化手法で確率や期待値が大きくなる実験条件・製造条件の候補を探索するとかです。

そして、選ばれた実験条件・製造条件で、次の実験をします。実験の結果得られた物性値が目標を達成したら、材料設計・製品設計終了です。もし目標を達成していなかったら、その実験データをデータベースに加えて、この流れを繰り返します。

以上のようなデータベースを活用した材料設計・製品設計や、プロセス設計・装置設計の研究の方向性としては、