応化先生と生田さんが k平均法 (k-means clustering) について話しています。

応化：今回は、k平均法 (k-means clustering) についてです。クラスタリングですね。

生田：階層的なクラスタリングですか？

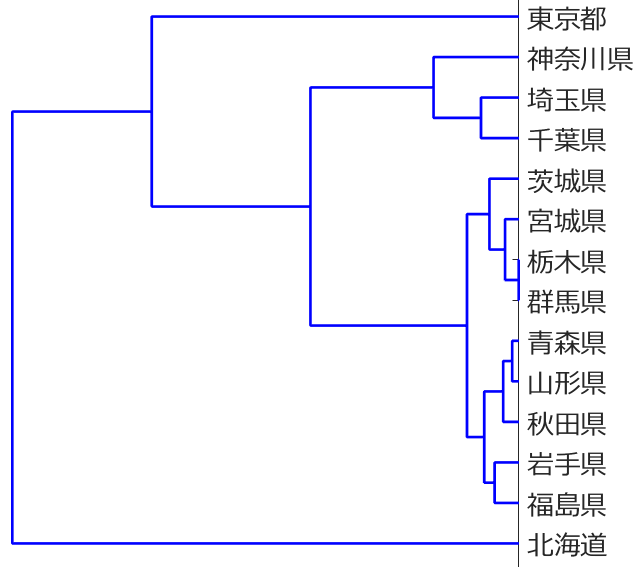
応化先生と生田さんが、階層的クラスタリング(クラスター分析)について話しています。応化：今日は階層的クラスタリングの話をします。生田：よろしくお願いします。クラスタリングって、クラス分類と名前の似ているアレですよね。応化：そうですね。もし違...

応化：いえ、今回は非階層的クラスタリングです。

生田：トーナメント表みたいなデンドログラムは書けないってことですか？

応化：そうです。k-means の結果としては、どのサンプルがどのクラスター(塊)かって情報だけです。

生田：クラスターの数はいくつになるんですか？

応化：それは、最初に自分で決める必要があります。

生田：クラスター数を最初に決めてからスタート？

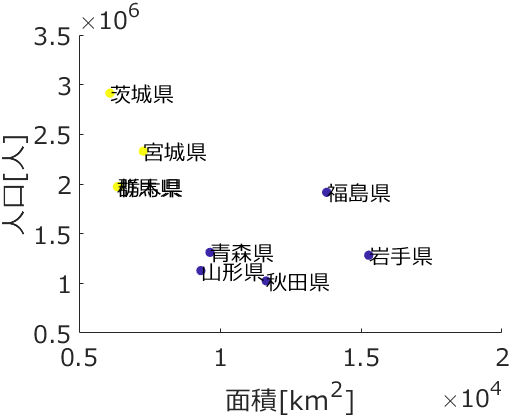
応化：はい、そういうことです。具体的に k-meansの結果を見てみましょう。階層的クラスタリングでも用いた都道府県のデータを使います。

階層的クラスタリング(クラスター分析)、近いクラスターを結合していく

応化：上のデータを用いて、クラスター数を 4 にして k-meansを行うと下のような結果になります。

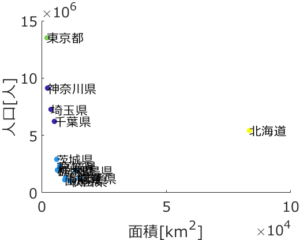
生田：名前の左にある ● の色でクラスターが分かれていますね。
・東京都クラスター
・北海道クラスター
・神奈川・埼玉・千葉県クラスター
・その他の県クラスター
という４つのクラスターになってます。東京都は人口が多いので、北海道は面積が大きいので、それぞれ一つのクラスターになって、関東でも人口の多い県である神奈川・埼玉・千葉県も一つのクラスター、その他が最後のクラスターですね。

応化：よく結果を解釈できていますね。

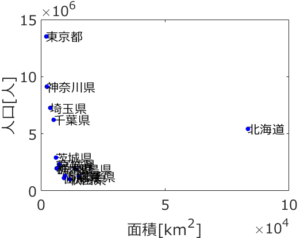
生田：クラスター数を 5 にするとどうなりますか？

応化：こうなります。

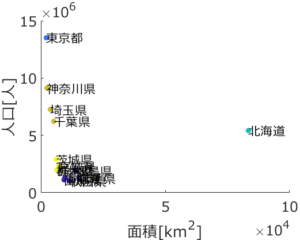
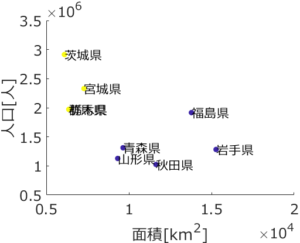
生田：下の拡大図を見ると、クラスター数が 4 のときは一つのクラスターだったのが、茨城・宮城・群馬・栃木県のクラスターと、福島・青森・山形・秋田・岩手県のクラスターに分かれています。クラスターの数によって結果が変わるんですね。

応化：そうなんです。では、どのような手順で k-means 法が行われているか説明します。

生田：お願いします！

k-means法の流れ

応化：最初に、ランダムに各サンプルにクラスター番号を割り当てます。

生田：東京都と北海道が、最初に一緒のクラスターになる可能性もあるってこと？

応化：そういうことです。全サンプルを、適当にクラスター数 (最初に決めた数) に分けてしまうんですね。

生田：最初は適当なんですね。

応化：次に、クラスターごとの中心を決めます。つまり、各クラスターに所属するサンプルの平均 (平均ベクトル) です。この平均ベクトルを、各クラスターの代表点とします。

生田：クラスターごとに平均を計算して、代表点とする、と。

応化：そして、各サンプルに割り当てていたクラスター番号をいったん白紙にします。

生田：もう、どのサンプルがどのクラスターか分かりませんね。

応化：そうですね。ただ、クラスターの代表点はわかります。なので、サンプルごとにすべての代表点との距離を計算し、その距離が小さい代表点のクラスターを、新たなクラスターとして割り当てます。

生田：サンプルごとに、一番距離が近い代表点のクラスターを割り当てるんですね。

応化：そういうことです。そしてまた、クラスターごとに平均ベクトル、つまり代表点を計算し、すべてのサンプルのクラスター番号を白紙にし、サンプルごとに一番近い距離の代表点のクラスターを割り当て、・・・というのを繰り返します。

生田：いつ終わりにするんですか？

応化：各サンプルのクラスターを白紙にする前と、その後に代表点との距離でクラスターを割り当てた後とで、すべてのサンプルのクラスター番号が変わらなかったら終了です。

距離はどうする？

生田：k-meansの一通りの手順はわかりました。代表点との距離を計算していましたが、距離ってなんですか？

応化：基本的にはユークリッド距離です。階層的クラスタリングでも出てきましたね。

階層的クラスタリング(クラスター分析)、近いクラスターを結合していく

生田：k-meansでも階層的クラスタリングと同じように、ユークリッド距離だけでなく、マハラノビス距離とかも使えるんですか？

応化：はい、使えます。もちろん、tanimoto係数などの類似度を非類似度に変換したものも使えますよ。このあたりは、階層的クラスタリングと同じですね。

最初に割り当てるクラスター番号はランダムでいいの？

生田：最初からの手順や距離についてわかりました！一つ気になるんですが、最初にサンプルごとに割り当てるクラスター番号はランダムでいいんですか？最初のクラスター番号が変わると、最後の結果も変わる気がするんですが・・・。

応化：指摘してくれた通り、最初にランダムに割り当てたクラスター番号によって、最終的なクラスタリングの結果が変わるときがあります。実は、結構あります。

生田：いいんですか？たまたま最初のクラスター割り振りに偏りがあるとき、変な結果になりそうな気がするんですけど・・・。

応化：うーん、こればっかりは仕方ないとしかいえないですね。ただ、うまく工夫しようとはしています。

生田：どういうことですか？

応化：最初のクラスターを割り当てる方法に、k-means++アルゴリズムというのがあります。ArthurさんとVassilvitskiiさんが2006年に発表しました。この方法では、最初にランダムにサンプルごとのクラスター番号を割り当てるのではなく、その後のクラスタリングがうまくいくような代表点を選ぼうとしています。

生田：クラスターの数だけある代表点ですよね。上の説明では、クラスター番号をランダムに割り振ってからクラスターごとに平均を計算して代表点としていましたが、それを最初に決めるんですか？

応化：はいそうです。まず最初に、ランダムにサンプルを選び、それを代表点とします。そして次の代表点は、すべてのサンプルについてその代表点からの距離の二乗を計算し、その値をすべての距離の二乗和で割った値を確率として、その確率にしたがって次の代表点を選びます。これを繰り返して、クラスターの数だけ代表点を決めるのです。

生田：どんなメリットがあるんですか？

応化：最初の代表点が、代表点ごとに離れた点になります。そのため、計算の収束も早くなり、最終的な結果も安定します。

生田：それはよさそうですね！ただ、やっぱりランダムに選ぶのはなくならないんですね。

応化：そうですね、k-means++アルゴリズムを使っても、k-means の実行ごとに結果が変わることがあります。