2021 年 6 月 3 日に、金子弘昌著の「Pythonで学ぶ実験計画法入門ベイズ最適化によるデータ解析」が出版されました。

講談社: https://www.kspub.co.jp/book/detail/5235300.html

Amazon: https://www.amazon.co.jp/dp/4065235308

Amazon(Kindle): https://www.amazon.co.jp/dp/B09C89HZRV

===[追記] 出版して約２年経過した 2023 年 4 月 12 日、Kindle 化学で１位、全体で３位に！

===

これまで他に、二冊の本「化学のための Pythonによるデータ解析・機械学習入門」と「Pythonで気軽に化学・化学工学」を出版しました。今回の本は、「化学のための Pythonによるデータ解析・機械学習入門」の流れを踏襲しています。その本では取り上げなかった実験計画法、適応的実験計画法、ガウス過程回帰、ベイズ最適化を、本書では重点的かつ丁寧に解説しています。もちろん、これまでの本と同様に、データ解析・機械学習、そしてプログラミングの初学者向けの内容です。データ解析・機械学習、特に本書でベイズ最適化を学ぶカギとなるガウス過程回帰を学ぶためには、数学の基礎も大事になるため、第８章では最低限の数学の基礎も説明があります。

さらに、第7章では Gaussian Mixture Regression (GMR) を用いた直接的逆解析法の説明もあります。

どうしてGMRやGTMRといったモデルの直接的逆解析法は良好な結果を生み出すのか？

回帰モデルを直接的に逆解析ができる、すなわち説明変数 X から目的変数 Y (Y が複数でもOK！) を直接的に推定できる手法である Gaussian Mixture Regression (GMR) や Generative Topogr...

サンプルプログラムやサンプルデータセットもありますので、対象のソフトウェアをインストールすれば (無料でインストール可能、インストール方法も本書に説明あり)、すぐに本書の内容を再現できます。さらに、サンプルデータセットの代わりに、ご自身のデータセットをサンプルデータセットと同じ形式で準備すれば、本書の内容をご自身の実験系に応用できます。

データ解析・機械学習やプログラミングの内容については、金子研の学部生、修士過程の学生、博士課程の学生にも確認してもらいながら精査しました。その精査も経て、よい仕上がりになったと思います。

ここでは本書の “まえがき”、目次の詳細、そして第１章と第２章を無料公開します (およそ 22000 字 + 図)。これらの無料公開をご快諾いただきました講談社の皆さまに感謝申し上げます。自信のある本だからこそ、ここまで無料公開できます。本書をご購入するときの参考になれば幸いです。それでは、よろしくお願いいたします。

まえがき

2020年1月、日本でも新型コロナウイルス (SARS-CoV-2) の感染者が確認され、その後まもなく、多くの大学において入構が禁止になりました。講義はオンラインで行われるようになります。そして、設備・装置・機器・薬品の揃った実験室でしかできない化学実験は、中断を余儀なくされました。執筆者も大学教員として、教育・研究の現場において学生と実験ができない現状にやるせない思いをしてきました。

大学だけでなく企業においても、テレワークが推奨され現場での実験を伴う研究・開発および製造は、縮小もしくは中断せざるを得ません。2020年限りで疫病が終息するとはいえず、新たなウイルスが猛威を振るう可能性もあります。現状のまま何も対策をしないと、疫病のたびに世界の教育・研究・開発・製造がストップし、いずれ衰退してしまいます。

さらに日本では、人口、特に生産年齢人口の急激な減少が、高い確度をもって現実のものになってしまいます。そのため、思いつく限りの実験条件の候補をすべて実験するような、従来型の人海戦術による絨毯爆撃的な研究・開発が困難になります。これでは日本のものづくりが衰退してしまいます。

以上の状況を打破し、教育・研究・開発・製造・ものづくりにイノベーションを起こすことが、本書の目的です。本書で解説する実験計画法および適応的実験計画法、そしてそれを高度化したベイズ最適化により、従来型の人海戦術による絨毯爆撃的な研究・開発を刷新し、開発する材料・製品の目的を明に指向した効率的な研究および開発に移行します。目指すべき材料や製品があるとき、その目標もしくは仕様を実現化するためにどのような実験レシピ・製造レシピにすればよいかが、事前に予測されます。このレシピに基づいて実験・製造することで、目標の材料や製品を獲得できます。結果的に実験回数・製造回数が少なくなり、効率的な材料設計・製品設計が可能です。本書ではこの未来に向けた内容になっています。

この本の使い方

実験計画法・適応的実験計画法について学習したい方は第 2 章をご覧ください。さらに第 3 章ではデータ解析手法・回帰分析手法の解説があり、適応的実験計画法の一つであるベイズ最適化につながるガウス過程回帰の説明もあります。第 4 章では回帰分析によって得られたモデルを運用するときに必要となる、モデルの適用範囲の解説があります。本書の内容は、高校卒業程度の数学の知識があることを前提としています。大学レベルの数学の基礎に関しては第 8 章に説明があります。必要に応じてご覧ください。その他、数学的な用語にはその都度補足説明を入れたり、参考文献を紹介したりしています。なお、第 1 章には、分子設計・材料設計・プロセス設計・プロセス管理における実験計画法・適応的実験計画法・データ解析・機械学習の活用についての説明があります。まだ実験計画法を適用する具体的な対象がない方は、実験計画法を活用するイメージを膨らませることができると思います。

さらに、実験計画法・適応的実験計画法・データ解析・機械学習に関して理解を深め、これらを実践的に活用するため、解説した手法を実際に実行するための、Python のサンプルプログラムもあります。サンプルプログラムを実行しながら内容を確認したい方は、第 8 章に必要なソフトウェアの説明、およびそれらのインストール方法や簡単な解説があります。本書で説明するすべての手法にサンプルプログラムが付いています。サンプルプログラムはすべて以下の Github のウェブサイトからダウンロードできます。

GitHub - hkaneko1985/python_doe_kspub: Pythonで学ぶ実験計画法入門　ベイズ最適化によるデータ解析

Pythonで学ぶ実験計画法入門　ベイズ最適化によるデータ解析. Contribute to hkaneko1985/python_doe_kspub development by creating an account on GitHub...

サンプルプログラムに関する本文中での説明は必要最小限にとどめています。ただし、サンプルプログラムを実行するだけで本書と同様の結果が得られ、さらにサンプルプログラムにおけるデータセットを変えるだけで、例えばご自身でお持ちのデータセットに対しても、同様の解析ができます。Python のプログラムについて詳細に調べたり検討したい場合は、本書の該当箇所を読んだり、サンプルプログラムのコメントを確認したり、「関数の名前 + python」でウェブ検索をしたりしてください。さらに解析を進めたい方は、「行いたい内容 + python」でウェブ検索するとよいでしょう。

第 5 章では、実験計画法・適応的実験計画法・ベイズ最適化を、Python の実践的なサンプルプログラムにより実際に行います。ぜひサンプルプログラムを実行しながら理解を深めていってください。さらに第 6 章には、分子設計・材料設計・プロセス設計・プロセス管理における実験計画法・適応的実験計画法・ベイズ最適化の応用事例があります。

第 7 章には、発展手法として、第 5 章のベイズ最適化の効果を上回ることが確認されている手法の解説および解析結果の説明があります。分子設計・材料設計・プロセス設計・プロセス管理のさらなる効率化のため、ぜひチャレンジしてみてください。

本書で扱う手法には、すべてサンプルプログラム・サンプルデータセットがあります。材料設計・分子設計・プロセス設計・プロセス管理の実習としても利用できます。そして、サンプルデータセットの同じ形式のデータセットをご自身で準備して、サンプルプログラムと同じフォルダ (ディレクトリ) に置けば、本書と同じ解析をそのまま実行することができます。

1 つ注意点として、基本的に本書で扱うデータセットの中身はすべて半角英数字で準備し、ひらがな・カタカナ・漢字などは使用しないことを前提としています。サンプルの名前や変数の名前などにひらがな・カタカナ・漢字を用いないよう注意してください。どうしてもひらがな・カタカナ・漢字を用いたい場合は、3.1 節におけるデータセットの読み込みに関する「参考」として対処法がありますのでご覧ください。

謝辞

本書の原稿の確認やサンプルプログラムの検証について、明治大学のデータ化学工学研究室 (金子研究室) の石田敦子さん、畠沢翔太さん、江尾知也さん、山田信仁さん、岩間稜さん、谷脇寛明さん、山影柊斗さん、山本統久さん、杉崎大将さん、池田美月さん、今井航彦さん、金子大悟さん、中山祐生さん、本島康平さん、湯山春介さん、吉塚淳平さんにご助力いただきました。ここに記し、感謝の意を表します。ありがとうございました。また、自宅で執筆していても暖かく見守ってくれた妻の藍子と、おとなしくしてくれた娘の瑠那と真璃衣に感謝します。

第１章データ解析・機械学習を活用した分子設計・材料設計・プロセス設計・プロセス管理

1.1 ケモ・マテリアルズ・プロセスインフォマティクス

データ解析・機械学習は、材料の研究・開発・製造といった色々な段階で利用できます (図 1‑1)。薬を例にして説明します (図 1‑2)。もちろん薬だけでデータ解析・機械学習が活用されているわけではありませんので、皆さまが対象とする材料に薬を置き換えて、お読みいただければと思います。

図 1‑1. 材料の研究・開発・製造におけるデータ解析・機械学習による分子設計・材料設計・プロセス設計

図 1‑2. 薬を例にしたケモインフォマティクス・マテリアルズインフォマティクス・プロセスインフォマティクス

鼻水やくしゃみが出るときに、薬を飲んで治った、という場合、基本的なメカニズムとしては、体の中の細胞にあるタンパク質と、薬に含まれる有効成分である化合物もしくはリガンドが結合して、薬としての効果を発揮する、ということになります。ここで重要となるのは、タンパク質と結合する化学構造を考えることです。このような分子設計において、データ解析・機械学習が活用されます。分子設計では、化合物の物性・活性・特性 Y と化学構造 X との間で、数値モデル Y=f(X) を、データベースを用いて統計的に構築します。このモデルを用いることで、化学構造からそれがもつ物性・活性・特性の値を予測できたり、物性・活性・特性が目標の値となるような化学構造を提案できたりします。分子設計のように化合物のデータを扱ってデータ解析・機械学習を行う研究分野のことをケモインフォマティクスやマテリアルズインフォマティクスと呼びます。

もちろん医薬品設計は非常に難しい課題ですが、薬の有効成分になるような分子が見つかったとしましょう。しかし、ここでゴールではありません。胃で効く薬にするのか、腸で効く薬にするのか、といったことを考えて錠剤を設計する必要があります。ここでもデータ解析・機械学習が活用されます。材料における製品品質としての活性・物性・特性 Y とその実験レシピ、つまり実験条件や製造条件 X との間で、数値モデル Y=f(X) を構築します。このモデルを用いることで、実験レシピから活性・物性・特性の値を予測できたり、活性・物性・特性が目標の値となるような実験レシピを提案できたりします。これは材料設計と呼ばれ、材料データを扱ってデータ解析・機械学習を行う研究分野も、ケモインフォマティクスやマテリアルズインフォマティクスと呼ばれています。

一つの錠剤ができたとします。ただ、ここでもゴールというわけではありません。たくさんの人に錠剤を届けるためには、錠剤をたくさん製造しなければならず、そのための反応器が必要です。反応器の設計のようなプロセス設計においても、データ解析・機械学習を活用することで効率的に設計できます。基本的には対象とするプロセスにおいてプロセスシミュレーションを行うことによって得られるデータセットを用いて、シミュレーション条件 X と生産量・製品純度などのシミュレーションの結果 Y との間で数値モデル Y=f(X) を構築します。このモデルを用いることで、シミュレーション条件からシミュレーションの結果を予測できたり、望ましいシミュレーション結果になるようなシミュレーション条件を提案できたりします。プロセス設計のようにプロセスのデータを扱いデータ解析・機械学習を行う分野をプロセスインフォマティクスと呼びます。もちろん反応器だけでなく、生成した化合物を精製するための蒸留塔などの、様々なプロセスを設計することが大切です。

設計したプラントを実際に建てたあと、プラントを運転するときには、プラントを制御して適切にプロセス管理をします。例えば錠剤を製造したあとに、この錠剤は効くが、あの錠剤は効かない、ということがあってはいけないため、高品質な製品を安定的に製造する必要があります。ただ、製品の濃度や密度など、測定に時間がかかったり、測定頻度が低かったりするプロセス変数を制御しようとすると、測定時間だけ制御に遅れが生じたり、適時制御することが困難になったりしてしまいます。ここでもデータ解析・機械学習を活用できます。測定に時間がかかったり、測定頻度が低かったりする測定が難しいプロセス変数 Y と、簡単に測定できるプロセス変数 X との間で数値モデル Y=f(X) を構築します。このモデルを用いることで、測定が簡単なプロセス変数の値から測定が困難なプロセス変数の値を推定できます。推定値をあたかも実測値のように用いることで、迅速なプロセス制御ができ、効率的なプロセス管理を達成できるわけです。さらに、プロセス変数の値が目標の値になるような操作条件をモデルから提案できます。このようなプロセス管理においてデータ解析・機械学習を活用する分野もプロセスインフォマティクスと呼ばれています。

以上のように、薬の分野でいうところの創薬から製薬まで、幅広い分野でデータ解析・機械学習を活用できます。もちろん他の材料でも、様々な分野でデータ解析・機械学習により材料の研究・開発・製造を効率化できます。

1.2 分子設計

また薬の例になりますが、分子設計において、IC₅₀ の値が小さい化合物を見つけることを考えます (図 1‑3)。IC₅₀ とは、標的としているタンパク質の機能を 50 % 阻害する化合物の濃度であり、この値が小さいほど薬になりやすいといえます (今回は薬を例にしており IC₅₀ で話を進めますが、もちろん薬以外も扱えますので、読者が対象としている物性や特性に置き換えてください)。そのため実験科学者は、IC₅₀ の値が小さくなるような化学構造を考えて、実際にその構造になるように分子を合成します。その後、IC₅₀ の値を測定して、その値が目標を達成していたら終了ですが、目標を達成しなかった場合には、再び IC₅₀ の値が小さくなるような化学構造を考えて、その分子を合成し、IC₅₀ を測定します。これを繰り返し行い、薬になりそうな化合物を探します。

図 1‑3. IC₅₀ (50% 阻害濃度) の値が小さい、薬になりやすい化合物の探索

医薬品を見つけるのは 20000 分の 1 という非常に低い確率といわれており [1]、医薬品設計は非常に難しい課題です。目標の IC₅₀ の値にならないことが続くと、次はどのような化学構造の分子を合成すればよいのか、と考えるでしょう。このようなときに、データ解析や機械学習を活用できます。仮定するのは IC₅₀ のような活性・物性・特性が測定された化合物群があることです。このとき、化合物の化学構造がわかれば計算できる情報を特徴量 (もしくは記述子・説明変数) X とおきます (詳細は 5.5 節)。一方で IC₅₀ のような活性・物性・特性など、実験したり合成したり測定しないと得られない情報を Y とおきます。この X と Y の間で数値モデル Y=f(X) を構築します。どのように X として数値化したりモデル Y=f(X) を構築したりするのでしょうか。最も単純な方法の一つに原子団寄与法があります (図 1‑4)。これは各分子の化学構造を、あらかじめ決めておいた原子団に分割して、それぞれの原子団の数を数え上げます。図 1‑4 のように、一つの分子に対して 1 行の数値で表されるため、例えば 100 化合物あれば、100 行になります。エクセルのシートが埋まるようなイメージです。これが X のデータセットです。Y のデータセットは化合物ごとの IC₅₀ の値であり、一列で表され、X のデータセット (のエクセルシート) の横に結合するイメージです。このデータセットを使って X と Y の間で数値モデル Y=f(X) を構築します。もちろん、図 1‑4の原子団寄与法における数値化の方法では、原子団の間の距離や分子の複雑性などの分子の詳細な情報を表現できないため、実際にはさらに複雑な特徴量を計算します。この辺りの分子の扱いについては、5.5 節において Python のサンプルプログラムがあります。

図 1‑4. 化学構造の数値化の例

X と Y との間で数値モデルを構築するする手法の一つに最小二乗法による線形重回帰分析 (Ordinary Least Squares, OLS) があります。まず図 1‑5 のように、先ほど数え上げたそれぞれの原子団の数に、何らかの値 (a₁, a₂, …) をかけて、それらをすべて足し合わせたもの、と仮定します。とりあえず図 1‑5 のような式で IC₅₀ は表されると決めてしまうわけです。次に a₁, a₂, … といった数値をデータセットから求めます。求め方は、IC₅₀の実測値 (図 1‑5 の左辺) と図 1‑5 の右辺で計算される IC₅₀の計算値との間の差 (誤差) が小さくなるように決める、といった方法です。a₁, a₂, … の数値が決まったあとの図 1‑5 の式が、いわゆる人工知能です。人工知能といっても、基本は中学校や高等学校で勉強する Y = aX + b であり、実際に用いられているのもそれを複雑にしたものといえます。もちろん図 1‑5 の式では X と Y との間の複雑な関係は考慮できません。OLS の詳細や他の (より複雑な) Y=f(X) を求める方法に関しては、第 3 章で説明します。

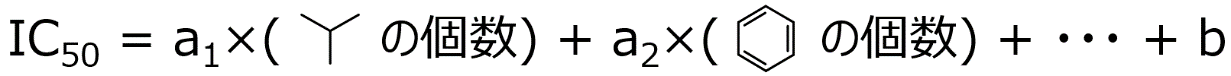
図 1‑5. Y = f(X) の例

図 1‑5 のようなモデル Y = f(X) が構築されたとします。このモデルを用いることで、実際に化合物を合成していなくても、その化学構造さえわかれば、その X の値を図 1‑5 のように計算し、それをモデルに入力することで、IC₅₀のような活性・物性・特性の値を推定できます。例えば ChemDraw [2] や MarvinSketch [3] のようなソフトウェアで化学構造を描画して、その分子がもつと考えられる活性・物性・特性の値を推定できます。人が分子を描くのには時間がかかるため、もちろん実験するよりは速いですが、多くても 1 日に数十個の化学構造の活性・物性・特性しか推定できないでしょう。ただ、例えばこちらのウェブサイト [4] にあるような化学構造のメインの骨格と置換基の両方を変化させながら化学構造を自動的に生成するプログラムを使うことで、1 日に数百万もの化学構造を作ることもできます。コンピュータの計算速度は速いため、これらの化学構造を X に数値化し、モデルに入力して活性・物性・特性の値を推定することも一晩で可能です。このように、実験するには現実的に不可能な数の化学構造でも、それらがもつと考えられる活性・物性・特性の値をコンピュータなら推定できます。良好な推定値をもつ化学構造を選択することで、有望な化学構造を獲得できます。

もちろんコンピュータで計算できる IC₅₀のような活性・物性・特性の値はあくまで推定値であるため、たとえそれが有望な値でも、本当にあっているかどうか実際に合成したり測定したりして検証する必要があります。実際、実験で検証された例もあります。薬の例でいえば、10 万化合物からモデル Y=f(X) を用いて CARM1 阻害剤となる化合物 15 個を選んだところ、その中の 3 化合物は乳癌細胞の増殖に対して実際に阻害活性を示しました [5]。20000 分の 1 の確率を 15 分の 3 に高めたと考えることができます。他の材料でも、ニッケル触媒の新規リガンドをモデルから提案することでクロスカップリング反応の選択性と収率が向上した例 [6] や、有機薄膜太陽電池の新しい材料をモデルにもとづいて設計することで光電変換効率が向上した例 [7] や、リチウムイオン電池の電解液を難燃化する材料をモデルで探索した例 [8] などが報告されています。

以上のように、データベースを活用することでデータ解析・機械学習により、活性・物性・特性が所望の値をもつ分子の設計を効率化できます。

1.3 材料設計

材料の活性・物性・特性は、化学構造だけでなく材料の作り方、つまり実験条件や製造条件によっても変化します。例えば高分子設計において、単量体 (モノマー) の化学構造だけでなく、そのモノマーの種類・組成比や、反応温度や反応時間といった重合条件によっても、高分子の各種の物性は変わります。実験条件・製造条件を X、材料の活性・物性・特性を Y として、X と Y との間で数値モデル Y=f(X) を構築することで、材料設計を効率化できます。

例えば表 1‑1 のような、実験条件 X (モノマー 1 の組成, モノマー 2 の組成, モノマー 3 の組成・重合温度・重合時間) とその実験結果である材料物性 Y のデータセットがあれば、分子設計と同様にして、例えば OLS で数値モデル Y=f(X) を構築できます (具体的な構築方法については第 3 章参照)。データセットがなければ、最初に作成する必要があります。実験条件・製造条件のいくつかの候補を決め、それらの条件で実験をして材料の物性を測定します。最初に実験する実験条件の候補を決める方法が実験計画法であり、詳しくは第 2 章で解説します。

表 1‑1. 材料設計におけるデータセットの例

	X1	X2	X3	X4	X5	Y
	モノマー1 の組成	モノマー2 の組成	モノマー3 の組成	重合温度	重合時間	材料物性
材料サンプル1	0.5	0.1	0.4	135	80	2.25
材料サンプル2	0.7	0.0	0.3	105	50	2.24
材料サンプル3	0.0	0.2	0.8	120	40	3.25
材料サンプル4	0.9	0.1	0.0	110	90	2.08
材料サンプル5	0.2	0.0	0.8	125	120	3.18
材料サンプル6	0.7	0.1	0.2	140	60	2.10
材料サンプル7	0.1	0.0	0.9	130	10	3.54
材料サンプル8	0.1	0.0	0.9	140	90	3.55
材料サンプル9	0.4	0.1	0.5	150	110	2.44
材料サンプル10	0.5	0.2	0.3	110	40	2.24
材料サンプル11	0.8	0.1	0.1	100	10	2.13
材料サンプル12	0.8	0.1	0.1	115	40	2.07
材料サンプル13	0.5	0.2	0.3	110	80	2.20
材料サンプル14	0.5	0.4	0.1	140	40	2.32
材料サンプル15	0.0	0.1	0.9	100	10	3.55
材料サンプル16	0.5	0.3	0.2	105	50	2.17
材料サンプル17	0.0	0.3	0.7	130	20	3.02
材料サンプル18	1.0	0.0	0.0	120	60	2.16
材料サンプル19	0.8	0.1	0.1	150	100	2.09
材料サンプル20	0.3	0.0	0.7	110	10	2.98

モデル Y=f(X) を用いることで、まだ実験していない実験条件の候補の値をモデルに入力し、実験の結果としての材料サンプルがもつと考えられる物性の値を推定できます。推定値が材料物性の目標値になる、もしくは近いような実験条件の候補を選択することで、次に行う実験を決められます。

実験の結果が得られたら、それが目標を達成していれば終了です。目標を達成していなかったら、実験条件の候補と実験結果をあわせたものをデータベースに追加して、再度モデルを構築します。新たに構築されたモデルを用いることで、次は別の実験条件の候補が選択されます。このように、モデル構築と次の実験の提案を繰り返すことを適応的実験計画法と呼び、詳細は2.3節で解説します。

1.4 なぜベイズ最適化が必要か

これまで、Y の推定値が目標値に近いような X の候補を次の実験条件の候補として選択する、といった説明をしていました。分子設計でも化学構造を選択するときは推定値を基準にしていました。しかし、Y の目標値と現状の Y の値との隔たりが大きいときに、適応的実験計画法、つまり実験とモデル構築を繰り返すことで目標を達成することを目指す場合には、そのような Y の推定値に基づいた選び方よりも、次に説明する「Y の目標を達成する確率」に基づいた選び方のほうが、実験回数が少なくて済む傾向があることがわかってきています。

「Y の目標を達成する確率」について図 1‑6を用いて説明します。Y (縦軸) として 1 つの物性、X (横軸) として 1 つの実験条件 (特徴量) とします。図 1‑6 の黒点のデータベース (6 サンプル) を用いて、図中の曲線のモデル Y=f(X) が構築されたとします。モデルについて言い換えると、X に色々な値を入力したときの、Y の推定値の集まりの曲線です。点線で囲まれたグレーの領域が Y の目標であり、この範囲に入るような X の値を探索したい場合を考えます。

単純に Y の推定値、つまり曲線だけに基づいて X の値を探すと、曲線が最も Y の目標に近づくのが、X の値が c₁ のときになります。しかし、図を見てもわかるように、X が c₁ の辺りにはサンプルがいくつも存在しており、これらのサンプルより Y の物性の値を向上させることは難しいと考えられます。このような状況においても、Y の推定値が良好な X の候補を選ぶと、c₁ となり、さらにはその次の実験条件の探索のときにも c₁ 付近の値となることが予想されます。物性の大きな向上が期待できない X の候補が選ばれ続けてしまい、毎回同じような実験をすることになってしまいます。そのため、c₁ よりは既存のサンプルから離れたところの、(失敗するかもしれませんが) 少し挑戦的な X の値が選ばれた方が、まだよさそうです。図 1‑6 のように X の特徴量が 1 つであれば、もう c₁ 付近には有望そうな候補はないことを、目で見て確認できますが、例えば 10 個など複数の特徴量があると、状況がよくわかりません。このような場合、Y の推定値だけでなく、推定値のばらつきを考えます。このばらつきは、ガウス過程回帰 (Gaussian Process Regression , GPR) によって計算でき、詳細は3.11節で解説します。

とにかく、Y の推定値ごとに、推定値のばらつきも計算できたとします。図 1‑6 の X の値が c₁ における Y のエラーバーのようなイメージです。これにより、ある 1 つの X の値における Y の推定結果を、ばらつきを標準偏差、推定値を平均値とした正規分布として表せます。X の候補それぞれにおいて、正規分布で Y を推定できるわけです。この正規分布は、確率密度関数 (Probability Density Function, PDF) であるため、ある範囲で積分すると、その範囲に入る確率として定義できます。つまり、Y の目標の範囲で積分する、つまり図 1‑6 のように Y の目標の範囲で囲まれる正規分布の面積を求めることで、その面積の値を「Y の目標を達成する確率」と考えられるわけです。次の実験条件、つまり X の値の候補を選択するとき、推定値が物性値に近い候補ではなく、正規分布を Y の目標の範囲で積分した値である「Y の目標を達成する確率」が高い候補を選びます。図 1‑6 においては、X の値が c₁ のときより c₂ のときほうが、面積が大きくなり、(推定値は目標から離れていても) c₂ が選ばれることになります。

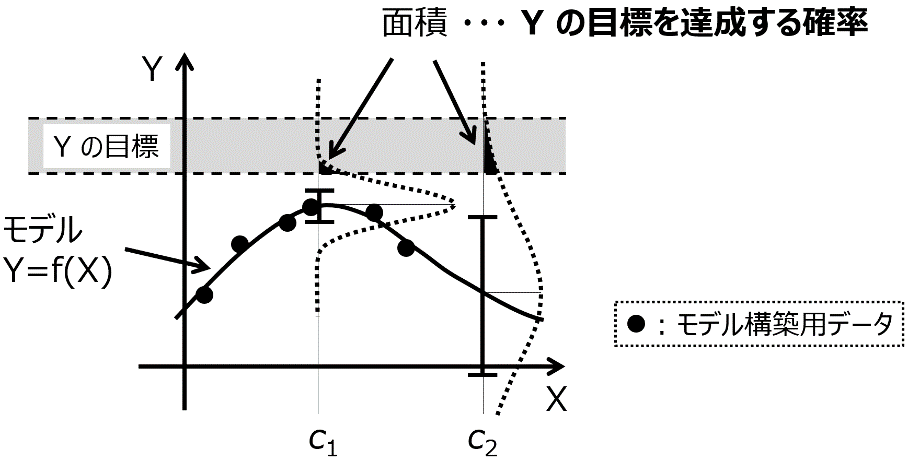
図 1‑6. Y の目標を達成する確率の概念図

このように次の実験条件の候補を選ぶことで、これまでのサンプルにおける物性の最良値と比べて、Y の目標が遠いときには、より外挿、つまりこれまでのサンプルにおける X の値から離れた候補が選ばれやすくなり、目標が近くなるにつれてより内挿が選ばれやすくなります。データベースにおける Y の値がまだ目標から遠いときには、挑戦的な実験条件が選択されるわけです。もちろん、目標に入る確率が比較的に高いというだけで、確実にその目標に入るわけではありません。確率が高くなるような候補を選び、それを実験することを繰り返すことで、Y の推定値だけで候補を選択するよりも、より少ない実験回数で Y の目標に達成できる、という理屈です。以上のような適応的実験計画法のことをベイズ最適化と呼び、詳細は 5.4 節で説明します。例えば分子設計や材料設計の課題において、ベイズ最適化により Y の推定値だけで候補を選ぶよりも少ない回数で、目標に達成できることが確認されています。

分子設計と材料設計を組み合わせることで、何を作るか (材料自体)、だけでなく、どう作るか (材料の作り方) も探索・最適化することが可能になります。

1.5 プロセス設計

反応器の形状・体積や反応器における反応温度・反応時間といったパラメータは、所望の反応器になるように、つまり生産量や製品の収率・純度が高いように、制御しやすいように設計されます。ただ、分子設計や材料設計と異なり、一度反応器を作って、目標の性能に達していなかったら、もう一度反応器を作り直す、といったことはコスト的・時間的に難しいです。そのため、基本的にはプロセスシミュレーションや CFD (Computational Fluid Dynamics) シミュレーションのような、コンピュータシミュレーションで反応器をはじめとした装置やプラントの計算をします。ただ、このシミュレーションにも計算時間がかかります。例えば、一回のシミュレーションに 1 時間かかるとします。反応器の大きさ・反応時間・反応温度など 6 つのパラメータがあり、パラメータごとに 10 の候補値があるとすると、すべての組み合わせの数は 10⁶ = 100 万になり、すべてのシミュレーションが終わるまで 100 万時間もかかってしまい、現実的ではありません。

そこで効率的にプロセスの設計をするため、データ解析や機械学習が活用されます (図 1‑7)。ただし、実施している内容としては、材料設計でも説明したような実験計画法や適応的実験計画法です。まず、コンピュータシミュレーションをする条件 (反応器の形状・体積や反応器における反応温度・反応時間など) Xを決めます。すでに X を振ってシミュレーションした結果があればそれを使いますし、まだなければ、実験計画法 (第 2 章参照) で最初にシミュレーションをする X の候補を求め (例えば 30 通り)、実際にシミュレーションをします。シミュレーションの結果 Y を用いて (X と Y のデータベースとし)、X との間でモデル Y = f(X) を構築します。このモデルを活用して次のシミュレーションにおける X の候補を決めます。例えば X のすべての候補が 100 万通りであれば、それらをモデルに入力して、100 万通りそれぞれの推定値およびそのばらつきを計算し、材料設計のときのような「Y の目標を達成する確率」を計算します。そして、確率が高いような X の候補を選択し、実際にシミュレーションを行います。この結果、実際に目標を達成していたら終了ですし、まだ達成していなかったら、シミュレーションの結果をデータベースに追加して、モデル Y=f(X) を再構築します。モデルの (再) 構築・X の候補の決定・シミュレーションといったサイクルを回すことで、目標を達成するようなシミュレーション条件を効率的に決めることができます。

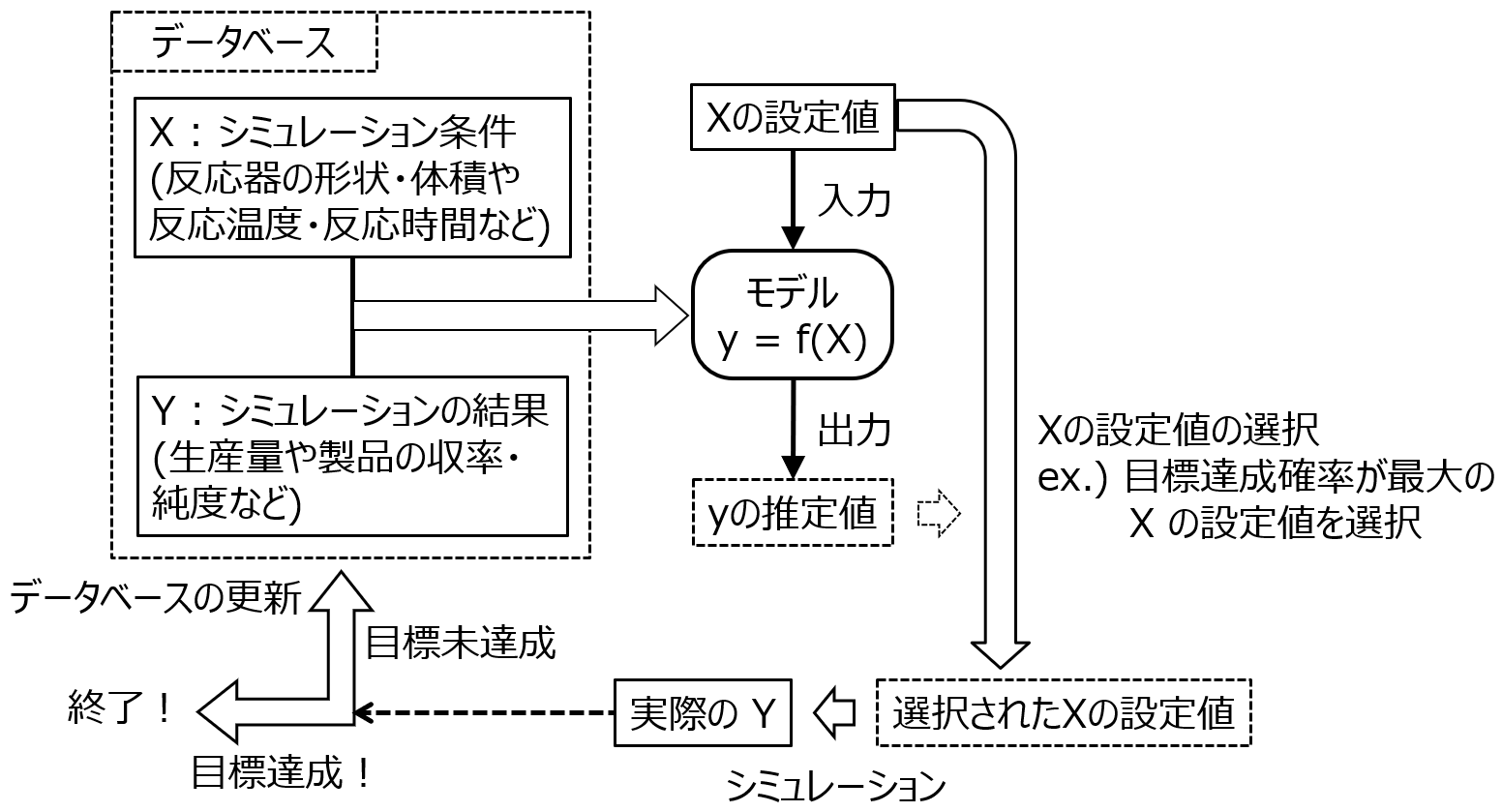
図 1‑7. 適応的実験計画法によるプロセス設計

1.6 プロセス管理

プロセス設計を経て製造された装置や化学プラントを運転するときは、プロセスを制御し、管理する必要があります。化学プラントやいろいろな装置では、センサーなどによって温度・圧力・流量といったプロセス変数の値が測定されています。例えば温度は、センサーによりリアルタイムに値を測定できるため、シャワーの温度を素早く 42 ℃にできるように、装置やプラントにおいて PID 制御などにより温度を迅速に制御する検討はできます。しかし、濃度や密度といった製品品質のように、製品をサンプリングして、研究室まで持っていき、測定装置にかけてしばらく待って測定結果が出てくる、といったような、測定時間がかかったり、頻繁には測定されていなかったりするようなプロセス変数の場合、制御に遅れが生じてしまいます。

このような状況において、ソフトセンサー (図 1‑8) が活用されます。まず、温度や圧力のように簡単に測定可能なプロセス変数を X とし、濃度や密度のように測定が困難なプロセス変数を Y とします。つぎに、Y は測定が困難といっても、例えば 1 日に 3 回とか 1 日に 1 回とかの頻度で、測定はされているため、X と Y の既存の測定データ (データベース) を作れます。ソフトセンサーとは、このデータベースを用いて、X と Y の間で構築された数値モデル Y = f(X) のことです。モデルの構築方法としては、例えば分子設計のところで説明したような OLS が用いられます。モデル (例えば図 1‑8の濃度 = 1.5×温度＋0.5×圧力) が得られてしまえば、X として温度・圧力などの値はリアルタイムに測定されているため、その値をモデルに入力することで、Y の値をリアルタイムに推定できます。この推定値をあたかも実測値のようにモニタリングすることで、実測値が得られない状況でも、迅速な制御を達成できます。

ソフトセンサーの活用の仕方を 4 つ紹介します。１つ目は先ほど述べたように、ソフトセンサーによる推定値を実測値の代わりに使用する、ということが挙げられます。推定値をモニタリングすることにより、迅速な制御ができたり、分析計の測定頻度を減らしたりできます。２つ目は、分析計と一緒にソフトセンサーを用いることで、分析計の故障を診断することです。例えば分析計の実測値と、ソフトセンサーの推定値が離れているとき、つまり誤差が大きいときに、分析計に何らかの異常が生じたと考えることができます。３つ目は、プロセス変数の間の関係を検討することです。例えば、図 1‑8 のような「濃度 = 1.5×温度＋0.5×圧力」というモデルが構築されたら、もちろん実際には温度や圧力の間にも相関関係があるため単純なことはいえませんが、温度や圧力は濃度に正に効いているだろう、と考えられます。最後は、ソフトセンサーを仮想的なプラントとみなすことです。X の時間変化の値をソフトセンサーに入力することで、その結果として Y の値がどのように変化するか推定できるため、実際に X の値を操作したときに、Y の値がどうなるかを検討できます。Y の設定値変更をするときに、なるべく効率的に制御するためには X の値をどのように時間変化させればよいかを検討できます。最後の点に関しては、適応的実験計画法を活用できます。

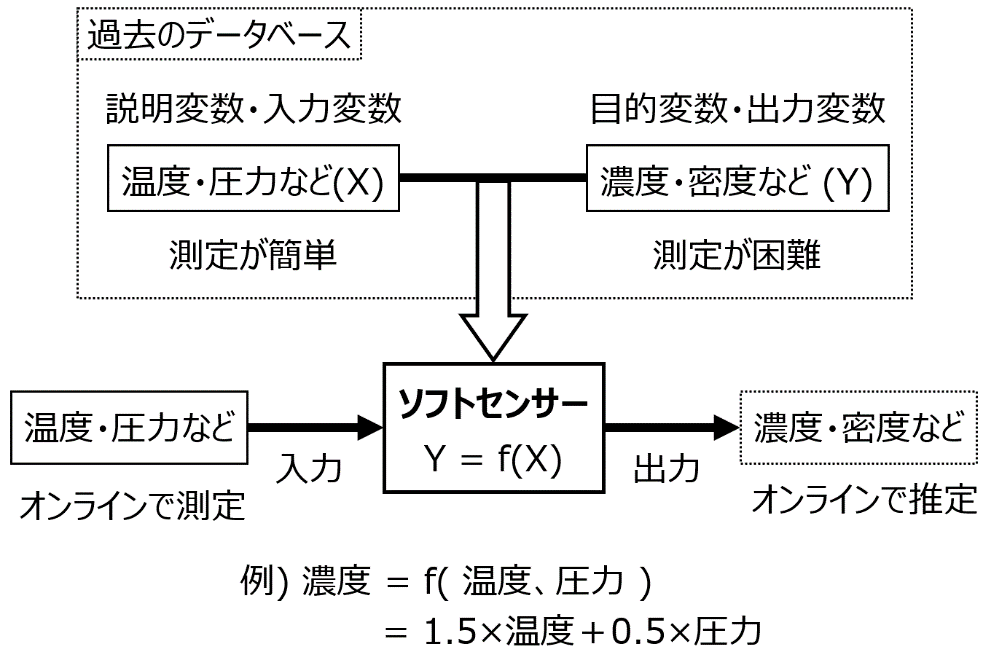
図 1‑8. ソフトセンサーの概要

1.7 データ解析・人工知能 (モデル) の本質

前節まで、ケモインフォマティクス・マテリアルズインフォマティクス・プロセスインフォマティクスとして、分子設計・材料設計・プロセス設計・プロセス管理をデータセットに基づいて実施する話をしました。共通して大事なことは、データ解析を行いモデル Y=f(X) を構築したり、構築されたモデルを適切に使用したりすることです。データに基づいて構築されたモデルのことを人工知能 (Artificial Intelligence, AI) と呼ぶこともあります。人工知能を作る、つまりモデルを構築するということは、形式的には、データの中に潜むパラメータ (X, Y) の間の関係を抽出している、といえます。ではこれは本質的に何を意味するのでしょうか。

例えば材料設計で高機能材料を設計するとき、実験条件を変えながら、目標を満たす材料を作るための実験条件・製造条件を決めることを考えます。このような状況において、実験をする研究者が高機能材料を作るために、その人のもつ情報・知識・知見・経験、ときには感性や勘、を使って、次の実験条件・製造条件を考え、実験をしています。その結果として、材料が作られ、その物性や活性の値が測定され、一つのサンプル (データ) になるわけです。もちろん一人の研究者だけでなく、複数の研究者によって、このような実験が行われることもあります。そのため、それらのデータを集めたデータセットの中には、たくさんの研究者の情報・知識・知見・経験・感性・勘がつまっています。

このデータセットを見ただけでは、研究者たちがどうして、どのような思考の結果で、そのような実験をしたのか理解することは難しいでしょう。つまり研究者の情報・知識・知見・経験・感性・勘を有効に活用できていません。データ解析をして人工知能を作る、すなわちモデル Y=f(X) を構築するということは、データセットの中から、研究者の情報・知識・知見・経験・感性・勘を抽出している作業といえます。

高機能性材料を作るプロセスにはサイエンスがあり、材料パラメータ・実験パラメータの間には (すべてのパラメータが手元にあることが前提ですが)、何らかの関係性があります。実際には、その関係性はわからないことが多いですが、研究者たちはそのサイエンスを把握しようといろいろと調査したり、自分で考えたり、考えたことを実験で検証したりしています。もちろん、実際は一人だけでなく複数の人たちが (同じ場所もしくは別の場所で) 研究しています。そのような研究者たちの考えたことが、データセットに反映されています。研究者たちの考えたサイエンスがデータセットに存在しているわけです。人工知能を作るというのは、そのサイエンスを抽出していることといえます。

作られた人工知能を使うというのは、過去の実験結果を再現させたり、いろいろな研究者の情報・知識・知見・経験・感性・勘がつながった結果をチェックしたりすることに対応します。もしくは、少しだけ情報・知識・知見・経験・感性・勘を外挿させます。その結果、有用な (目標の物性値に近づく) 材料が得られる可能性が出てきます。

第２章実験計画法

高機能性材料を開発することを考えます。材料設計をするためには、例えば表 1‑1 のようなデータセットが必要です。つまり、モノマー 1 の組成, モノマー 2 の組成, モノマー 3 の組成・重合温度・重合時間といった実験条件のパラメータ X に関して、いくつかの値の組み合わせで実験して、その実験結果である材料物性 Y のデータセットがないと、前章で概要を説明したようなデータ解析ができません。データ解析を実施することを前提としたときに、良好なモデル Y=f(X) を構築できるように、最初に実験すべき適切な X の候補を決める方法が、実験計画法 (Design of Experiments, DoE) です。実験計画法によって提案された実験条件で実験し、Y を測定することで X と Y のデータベースを作成し、モデル Y=f(X) を構築すれば、Y の値が良好になるような次の実験条件を、モデルから提案できます。提案された実験条件での実験結果が、Y の目標を達成していれば終了となりますが、達成していなければ、実験結果をデータベースに追加して、再度モデル Y=f(X) を構築します。モデル構築、新たな実験条件の提案、実験、実験結果のデータベースへの追加を繰り返しながら、Y の目標を達成する材料を作るための実験条件を探索することを、適応的実験計画法 (Adaptive Design of Experiments, ADoE) と呼びます。本章では、実験計画法と適応的実験計画法について説明します。

2.1 なぜ実験計画法か

A, B, C, D を何らかの化合物として、化学反応 A + B → C + D における C の収率を上げることを考えます。収率が最も高くなる実験条件を見つけることが目標となります。

実験条件の 1 つである反応温度を 25℃ にして実験することを考えます。人間は精密機械ではありませんし、実験するときの環境が完璧に同じになることはありえませんので、同じ実験条件で実験しても、結果は少しずつ異なります。つまり、収率の値はばらつきます。そこで同じ実験条件で何回か、例えば 3 回実験します。

もちろん、他の反応温度の値のほうが収率は高くなる可能性があります。そこで 25 ℃だけでなく、別の反応温度の値にして実験します。例えば、反応温度が 20 ℃, 30 ℃, 35 ℃, 40 ℃, 45 ℃, 50 ℃の場合でも実験します。(25 ℃を合わせて) 7 通りの反応温度がありますので、実験の回数は 3 × 7 = 21 回となります。

さらに、反応温度だけでなく、反応時間や触媒量も変更すると、収率がより高い実験条件がある可能性があります。反応時間・触媒の量もそれぞれ 7 通りあるとすると、反応温度・反応時間・触媒の量について、すべての実験条件の組み合わせで実験すると、実験の回数は 3×7×7×7 = 1029回もの数になります。すべて実験するのは現実的ではありません。

ここで考え方を変えます。もちろん、収率が最も高くなる実験条件を探索することが最終的な目標ですが、その前の目標として、下のモデルを求めることを目標にします。

収率 = f(反応温度、反応時間、触媒量) (2.1)

f は何らかの数式であり、「化学反応モデル」と名付けます。f に反応温度の値・反応時間の値・触媒量の値を入力すると、収率の値が出力されます。このモデルがあれば、反応温度・反応時間・触媒量を変えたときに収率がどうなるか、実験せずに確認できます。化学反応のシミュレーションができるわけです。そして、シミュレーションの結果、収率が最も高い実験条件で、実際に実験することが可能となります。

以上の化学反応の例のように、高機能性材料を作るための実験をしたり、装置を設計するために時間のかかるコンピュータシミュレーションをしたりすることがあります。実験をするときは、どのような原料を使用するか、それぞれの原料をどのくらい用いるかをはじめとして、いろいろな実験条件をあらかじめ決める必要があります。実験レシピを決めるわけです。シミュレーションをするときにも、あらかじめいろいろなパラメータの設定値を決める必要があります。目的の高機能性材料を作るための実験レシピや、目的の装置となるようなパラメータの設定値がわからないときは、実験条件をいくつか振って実験したり、パラメータの設定値をいくつか振ってシミュレーションをしたりします。実験条件の数やパラメータの数が多いとき、そして実験条件ごと、パラメータごとに候補の値もしくは種類が多いときには、すべての組み合わせで実験したり、シミュレーションをしたりするのは現実的ではありません。なるべく少ない実験回数、シミュレーションの回数で、目的の高機能性材料を作るための実験レシピや、目的の装置となるようなパラメータの設定値を効率的に探したいわけです。

このときに、実験条件やパラメータ X と、実験の結果やシミュレーションの結果 Y との間で、モデル Y=f(X) を構築することを考えます (シミュレーションをするときには、元々何らかのモデルがあるわけですが、それよりも簡易的なモデルとお考えください)。このモデルがあれば、X の値を入力して Y の値を計算することが、実験をしなくても、(時間のかかる) シミュレーションをしなくても、可能です。そのため、例えば 100 万通りのような、たくさんの X の値の候補をモデルに入力することで Y の値を計算し、その計算された Y の値が良好な X の値を選択する、といったこともできます。実験なしに、シミュレーションなしに、目的の高機能性材料を作るための実験レシピや、目的の装置となるようなパラメータの設定値を効率的に探せるわけです。

ここでは、モデル Y=f(X) が重要です。なるべく良好な (精度の高い) モデルが必要です。実験計画法により、良好なモデル f を構築するための、実験における最初の実験条件の候補や、シミュレーションにおけるパラメータの最初の設定値の候補を選択します。

2.2 実験計画法とは

化学反応において反応温度・反応時間・触媒量 X を収率 Y が最大になるように最適化する例に戻ります。式(2.1) のモデル f について、例えば以下のようなモデルの形式が考えられます。

収率 = a₁×反応温度＋a₂×反応時間＋a₃×触媒量＋定数項 (2.2)

a₁, a₂, a₃ には何らかの数値が入ります。このように、それぞれのパラメータに何らかの値を掛けて、すべて足し合わせた形のモデルを、線形モデルと呼びます。

正しいかどうかはさておき、収率と反応温度・反応時間・触媒量との間の関係が、式(2.2) の線形モデルで与えられると仮定します。仮定した上で、式(2.2) の a₁, a₂, a₃ を求めるための実験を行うことを考えます。求めるものは a₁, a₂, a₃ の 3 つであるため (式(2.2) では定数項も求める必要がありますが、詳しくは 3.5 節で説明する通りここでは気にしなくて構いません)、収率・反応温度・反応時間・触媒量の組み合わせのデータ (サンプル) が、最低 3 つあれば、a₁, a₂, a₃ を求められます。最低 3 回だけ実験すればよい、ということです。実際は、実験結果にばらつきがあることもあり、3 回より多くの実験をして a₁, a₂, a₃ の値を求めることが一般的です。

実験計画法は、a₁, a₂, a₃ の値を求めるための実験の、反応温度・反応時間・触媒量の値の組み合わせにおける、いくつかの候補を決める方法です。実験計画法によって決められたいくつかの実験レシピによって実験するわけです。

では実験計画法により、反応温度・反応時間・触媒量の値の組み合わせにおける、いくつかの候補をどのように決めるのでしょうか。

目的の高機能性材料を作るための実験レシピや、目的の装置となるようなパラメータの設定値を効率的に探すためには、モデル Y=f(X) が重要であり、なるべく良好な (精度の高い) モデルが必要です。そこで、実験条件 X と収率 Y との間で、良好な回帰モデルが構築できるように、最初の実験候補を選択することを考えます。

回帰モデルが良好かどうか確認するためには、実際に回帰モデルを具体的に求める、つまり式(2.2) の線形モデルでいえば a₁, a₂, a₃ を計算する必要があります。式(2.2) の線形モデルを用いるとき、右辺で計算できる Y の計算値と、左辺における実際の Y の値 (実測値) とがなるべく一致するように、a₁, a₂, a₃ を計算します。この計算方法の詳細は 3.5 節で説明します。ここでは答えだけ示すと、ベクトル a を

a = (a₁, a₂, a₃)^T (2.3)

とするとき (右肩の ^T は、ベクトルや行列を転置することを表す記号です。ベクトルの表記方法を含めて、詳細は 8.1 節で説明します)、a は以下の式で計算できます。

a = (X^TX)^-1X^Ty (2.4)

ここで X は縦に実験サンプル、横に X (実験条件) が並んだ行列であり、y は実験サンプルごとの Y (収率)の値が縦に並んだ縦ベクトルです (右肩の ^-1 は逆行列であることを表します。行列の表記方法を含めて、詳細は 8.1 節で説明します)。ここで言いたいことは、モデルを構築する、つまり a を計算するためには、y つまり実験したあとのデータが必要ということです。しかし、まだ実験していない、Y のデータがない状況で、どのように良好なモデルであると判断すればよいのでしょうか。

式(2.4) における

(X^TX)^-1 (2.5)

の部分に着目します。式(2.5) の逆行列 (詳細は 3.5 節) を計算できないと、式(2.4) の a が得られず、回帰モデルを求めることができません。また、逆行列を計算できない状況に近いと、良好なモデルの構築は困難になってしまいます。逆行列が計算できない状況とは、

X^TX (2.6)

の行列式 (詳細は 8.1 節) の値が小さい状況です。そこで実験計画法では、良好なモデルを構築できる X を得るため、X^TX の行列式が大きくなるような実験条件の候補を選びます。こうすることで実験結果 (収率 Y のデータ) がなくても、実験条件 X のデータセットのみから候補を選ぶことができます。なお、今回最大化する X^TX の行列式のことを D 最適基準と呼びます。言い換えると実験計画法では、以下の①②を同時に満たすように X の候補を決めます。

類似した実験条件の候補がない
X (特徴量) の間の相関係数の絶対値が小さい (特徴量同士が類似しない)

X の候補を決める方法として、古くから直交表 [9] が使われてきましたが、直交表では各 X の値や実験候補の数を自由に決めることが難しいため、ここでは D 最適基準に基づいて実験条件の候補を選択する方法を用います。X^TX の行列式である D 最適基準は実験計画法において実験候補を選択するために最適化 (今回は最大化) するパラメータの一例であり、他にも A 最適基準や E 最適基準など [10] があります。

このように実験計画法では、まだ実験結果や (時間のかかる) シミュレーションの結果である Y のデータがない状況において、(Y のデータを得るために) 最初にいくつかの実験やシミュレーションを行う際に、良好なモデル Y=f(X) を構築できるように実験条件やシミュレーションにおけるパラメータ X の候補を決めます。

具体的に実験条件の候補を決める手順は 5.1, 5.2 節で説明します。そして、実際に実験条件の候補を求め、csv ファイルとして保存する Python のサンプルプログラムについても解説します。なお、サンプルが実験条件やコンピュータ計算におけるパラメータのように最初から数値化されていない化学構造の場合でも、あらかじめ化学構造を数値化しておくことで、実験条件やコンピュータ計算におけるパラメータと同様に、実験計画法により最初に実験すべき化学構造を提案できます (詳細は 5.5節参照)。

2.3 適応的実験計画法

化学反応において反応温度・反応時間・触媒量 X を収率 Y が最大になるように最適化する例に戻ります。5.1, 5.2 節の実験計画法で求めた実験条件の候補で実験することで、(X のデータに加えて) Y のデータが手に入ります。X, Y のデータセット、つまり X および y を用いて、モデル Y=f(X) を構築できます。式(2.2) の a₁, a₂, a₃ の値を、式(2.4) により求められるわけです。

もし、Y と X の間の関係が、式(2.2) のように単純に Y に対して X それぞれが独立して直線的に関係していると (Y と X の間は線形関係と) 仮定できなかったり、実際に式(2.2) を仮定してモデルを構築して (a₁, a₂, a₃ の値を求めて) Y の値を計算したら、計算された Y の値と実際の Y の値との誤差が大きかったりするとき、X と Y の間に非線形関係があると考えてモデルを構築するとよいです。最も単純に X と Y の間の非線形性を表現する方法の一つは、X に、各 X を二乗した項 (二乗項) と、2 つの X の間で掛け合わせた項 (交差項) を追加する方法です。交差項は、一般的には 2 つの X のすべての組み合わせで準備します。今回の例でいえば、反応温度・反応時間・触媒量に、二乗項として (反応温度)²・(反応時間)²・(触媒量)² の 3 変数を、交差項として反応温度×反応時間・反応時間×触媒量・反応温度×触媒量の 3 変数を追加します。これによりモデル Y = f(X) は以下のようになります。

収率 = a₁×反応温度＋a₂×反応時間＋a₃×触媒量＋a₄×(反応温度)²＋a₅×(反応時間)²＋a₆×(触媒量)²＋a₇×反応温度×反応時間＋a₈×反応時間×触媒量＋a₉×反応温度×触媒量＋定数項 (2.7)

そして、式(2.2) と同様にして (詳しい計算過程は 3.5 節で説明します) a₁ から a₉ までの値を計算します。つまり、式(2.3) と同様にベクトル a を

a = (a₁, a₂, a₃, a₄, a₅, a₆, a₇, a₈, a₉)^T (2.8)

として、X を縦に実験サンプル、横に X (実験条件) およびその二乗項と交差項が並んだ行列にして、式(2.4) により a を計算します。式(2.7) のモデルのほうが、式(2.2) のモデルより良好な推定性能であることもあります。モデルの良し悪しを評価する方法の詳細は 3.6 節で説明します。

式(2.2) や式(2.7) といったモデルを構築したら、まだ実験していない X の多数の候補について、X の値をモデルに入力して、Y の値を推定します。推定された値が良好な (ここでは Y が収率なので値が大きな) 実験条件の候補を選択するわけですが、あくまで Y の “推定” 値であるため、その値をどのくらい信頼できるか (推定値が当たっているかどうか) わかりません。そこで、モデルの適用範囲 (Applicability Domain, AD) というものを考えます。AD の詳細については第 4 章をご覧ください。AD を考慮することで、Y の推定値を、モデルを構築したときのサンプルにおける推定誤差と同程度の誤差と信頼できる、X の値がわかります。Y の推定値が良好で、かつ推定値を信頼できる X の候補を選択できるわけです。

このように X の候補を選択し、その候補で再び実験を行います。Y のデータが得られるわけです。なお、X の複数の候補を選択するときには、それらが類似していない候補を選択しましょう。具体的なやり方は 5.4.1 項をご覧ください。

実験後に Y のデータが得られたら、X と Y の組のサンプルをデータベース (式(2.4) の X および Y) に追加して、再度、式(2.2) や式(2.7) のような回帰モデルを構築します。つまり、a₁, a₂, … を計算し直します。再構築されたモデルを用いて、まだ実験していない X の候補を、AD を考慮した後にモデルに入力して Y の値を推定し、Y の推定値が良好な X の候補を選択します。このように、モデルを用いて次の実験条件 X の候補を選択し、実際に実験し、実験結果を用いてモデルを再構築する、といったことを繰り返して、収率 Y が大きくなる X の候補を探索します。

以上のように、下の 1. 2. 3. を繰り返して、実験の結果や (時間のかかる) シミュレーションの結果 Y が良好な値になるように、もしくは目標の値となるように、実験条件やパラメータ X の候補を探索することを、適応的実験計画法 (Adaptive Design of Experiment, ADoE) と呼びます。

モデルを用いた次の実験条件やパラメータの候補の選択
実験やシミュレーション
実験の結果やシミュレーションの結果を用いたモデル構築

上の適応的実験計画法の説明では、上の 1. で次の実験条件やパラメータの候補の選択するとき、X の値をモデルに入力して Y の値を推定し、その推定値が良好な値となる X を選択しました。しかし、1.1 節の図 1‑6 を用いて説明したように、Y の推定値が良好な X の候補を選ぶと、物性の大きな向上が期待できない X の候補が選ばれ続けてしまい、毎回同じような実験をすることになってしまう可能性があります。そこで図 1‑6 では、Y の推定値とそのばらつきに基づいて、「Y の目標を達成する確率」を計算しました。

このように適応的実験計画法において、実験条件の候補やパラメータの候補ごとに Y の推定値だけでなく推定値のばらつきも考慮して指標 (獲得関数) の値を計算し、その値が大きい候補を選択する方法をベイズ最適化 (Bayesian optimization) と呼びます。ベイズ最適化を用いることで、データベースにおける Y の最良値と比べて、Y の目標が遠いときには、より外挿、つまりこれまでのサンプルにおける X の値から離れた候補が選ばれやすくなり、目標が近くなるにつれて内挿が選ばれやすくなります。データベースにおける Y の値がまだ目標から遠いときには、挑戦的な実験条件が選択されるわけです。もちろん、目標に入る確率が高いといっても、確実にその目標に入るわけではありません。確率が高くなるような候補を選び、それを実験することを繰り返すことで、Y の推定値だけで候補を選択するよりも、より少ない実験回数で Y の目標に達成できる可能性があります。ベイズ最適化の詳細は 5.4 節で説明し、そこでベイズ最適化を実行するための Python のサンプルプログラムおよびその使い方も紹介します。

2.4 必要となる手法・技術

実験計画法・適応的実験計画法・ベイズ最適化を行うためには、実際に実験したり (時間のかかる) シミュレーションをしたりすることを除いて、データ解析・機械学習の中でも特に回帰分析とモデルの適用範囲 (Applicability Domain, AD) が必要です。それぞれ第 3 章と第 4 章で説明しています。また回帰分析を実行したり、AD を設定したり、大量のデータ (仮想的な実験条件の候補やシミュレーションのパラメータの候補) を処理したりするため、プログラミング技術が必要です。本書ではプログラミング技術を補填するため、それぞれを実行するための Python のサンプルプログラムを配布しています。こちらの URL [https://github.com/hkaneko1985/python_doe_kspub] からダウンロード可能です [11]。8.4 節や [12,13] のウェブサイトを参考にして Anaconda [14] というパッケージをインストールしてから、Spyder というソフトウェアを起動すれば、Python のサンプルプログラムを実行できます。また実行するときに必要なサンプルデータセットも一緒に配布しています。第 3 章、第 4 章、第 5 章を読みながら、一緒に Python プログラムを実行するとよいでしょう。さらに、サンプルデータセットの形式を参考にして、ご自身の実験系やシミュレーションにあわせてデータセットを作成すれば、そのデータセットに対して同じプログラムで実行することができます。もちろん、プログラムをご自身で変更してカスタマイズしていただいても構いません。

以上です。

質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。