たとえば、ランチにラーメン屋さんにいくことを考えましょう。おいしくて、安いラーメンが食べられるところを探しますよね。いろいろと調べた結果、下の図のようになりました。一つ一つの ○ がラーメンです。

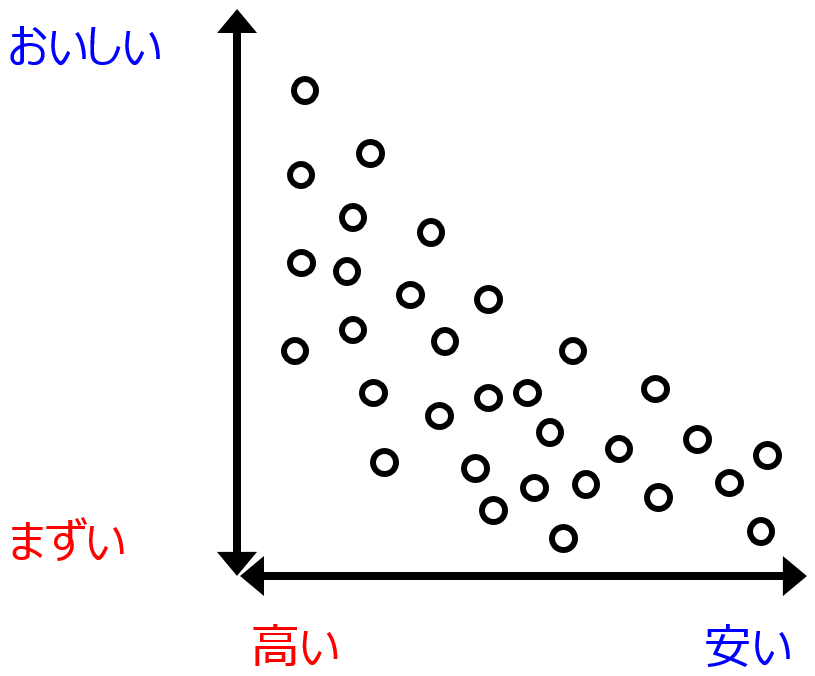
おいしくて安いラーメンを探しているのに、おいしいラーメンほど、値段が高い傾向があります。そして、安いラーメンほどおいしくない、といった感じです。このように、ある基準での評価と、別の基準での評価が両立しないとき、それらの基準はトレードオフの関係にある、といいます。あちらを立てればこちらが立たず、といった感じです。

トレードオフの関係は、いろいろなところにあります。

賃貸で家を探すとき、駅まで歩いてかかる時間の短さと家賃の安さの関係
印刷するとき、印刷する速さと印刷のキレイさの関係
アトラクションに乗るとき、人気度と行列の短さの関係
テトリスで、得点の高さとプレイ時間の長さの関係 (積み上げて長い棒を待つと高得点を狙えるが、ゲームオーバーになる確率も高くなってしまう)

とかです。トレードオフの関係にあるなかで、適したものを選択することが求められます。

このようなとき、パレート最適解を考えるとよいです。パレート最適解とは、先ほどのラーメンでいうところの、下の青丸のようなラーメンです。

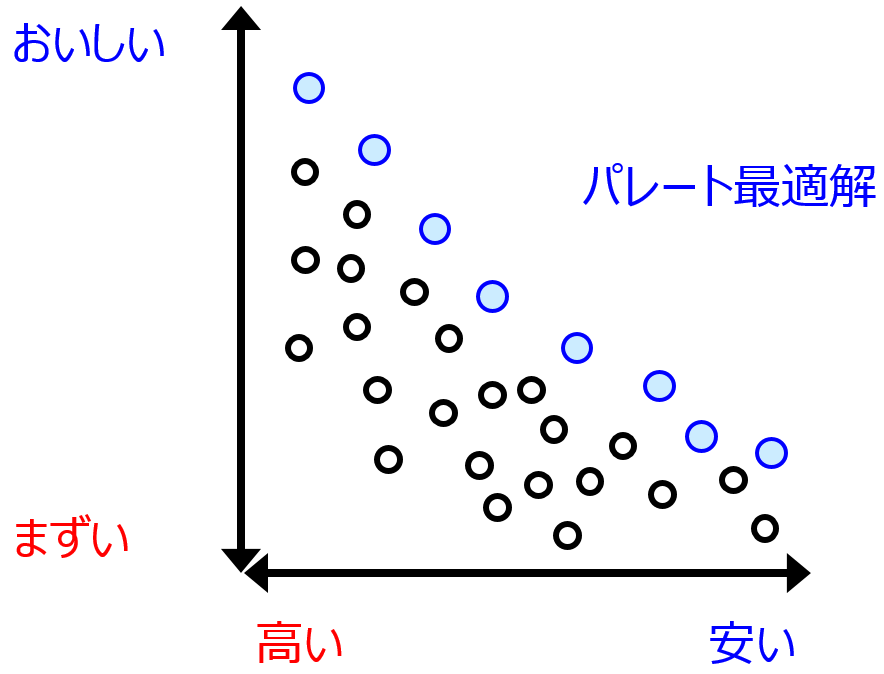
パレート最適解とは具体的にどのような解のことでしょうか。逆に、パレート最適解でないものを考えると分かりやすいです。それは、トレードオフの関係にある基準をすべて改善できる解が他にあるもの、です。そのようなものがないとき、パレート最適解といいます。

ラーメンは、パレート最適解から探せばよいわけです。

もちろん、ラーメンを選ぶにしても、おいしさは一つの基準だけで測れませんし、お店の雰囲気を重要視する人もいると思います。基準は２つより多くあるわけです。他のケースにおいても、たくさん基準があることが多いため単純ではありませんが、基本的にはパレート最適解のみを候補とすることで、一つ選ぶときの見通しがよくなります。

基準をどれだけ把握できるか、も重要です。どんなことにも、メリットもあれば、デメリットもあるものです。コピペのときもそうでした。