分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と材料の物性・活性・特性や製品品質 y との間で数理モデル y = f(x) を構築し、構築されたモデルを用いて x の値から y の値を予測したり、y が目標値となるような x を設計したりします。予測精度が高いモデルを構築するために、そもそも そのモデルの予測精度はどれくらいか、評価する必要があります。
回帰分析を対象としたときに、回帰モデルの予測精度の評価をする方法として、
- テストデータを用いた検証
- バリデーションデータを用いた検証
- クロスバリデーションによる検証
- ダブルクロスバリデーションによる検証
- y-randomization による検証
- MAECCE
があります。今回はこの辺りを整理します。
回帰モデルを構築するといっても、モデル構築手法の中には、データ解析者があらかじめ設定する必要のあるパラメーターであるハイパーパラメータがあるものもあります。例えば PLS の成分数やガウシアンカーネルを用いた SVR における C, ε, γ です。
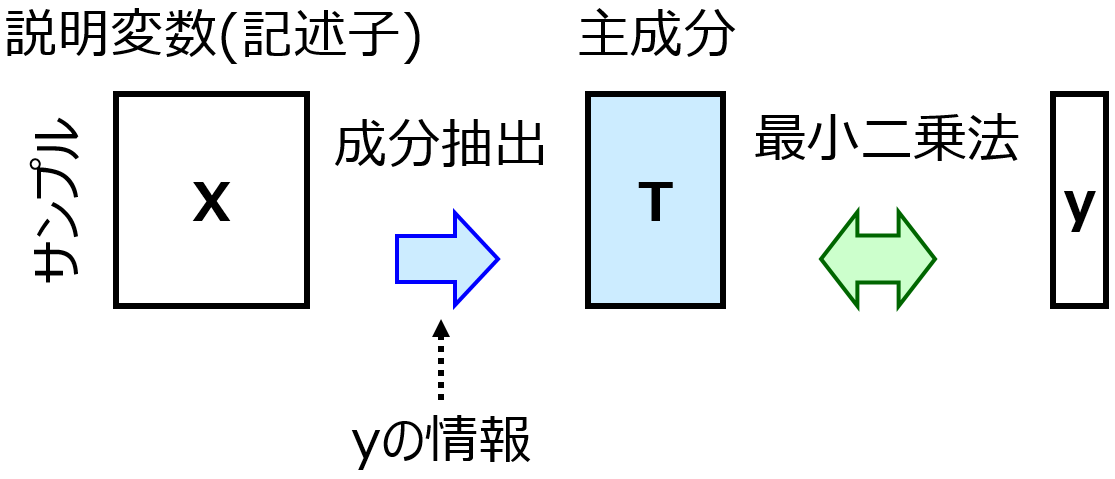

予測精度の高いモデルを構築するためのハイパーパラメータの候補を決めるのに用いる方法が、
- バリデーションデータを用いた検証
- クロスバリデーションによる検証
です。例えばバリデーションデータにおける y の予測値やクロスバリデーションによって得られる y の予測値と、y の実測値との間で r2, RMSE, MAE を計算し、r2 の値が大きくなるハイパーパラメータの候補や、RMSE や MAE の値が小さくなるハイパーパラメータの候補を選択します。

適切なハイパーパラメータの候補を選択して回帰モデルを構築することはできますが、そもそも色々な回帰分析手法がある中で、どのようなデータセットにも、どのような y にも合うベストな手法が存在するわけではありません。データセットごと、y ごとに適切な回帰分析手法を選ぶ必要があります。ここでの選択に用いられるのが、
- テストデータを用いた検証
- ダブルクロスバリデーションによる検証
です。テストデータにおける y の予測値やダブルクロスバリデーションによる y の予測値と、y の実測値との間で r2, RMSE, MAE を計算してそれらの値に基づいて評価したり、y の実測値と推定値の散布図を見て評価したりします。

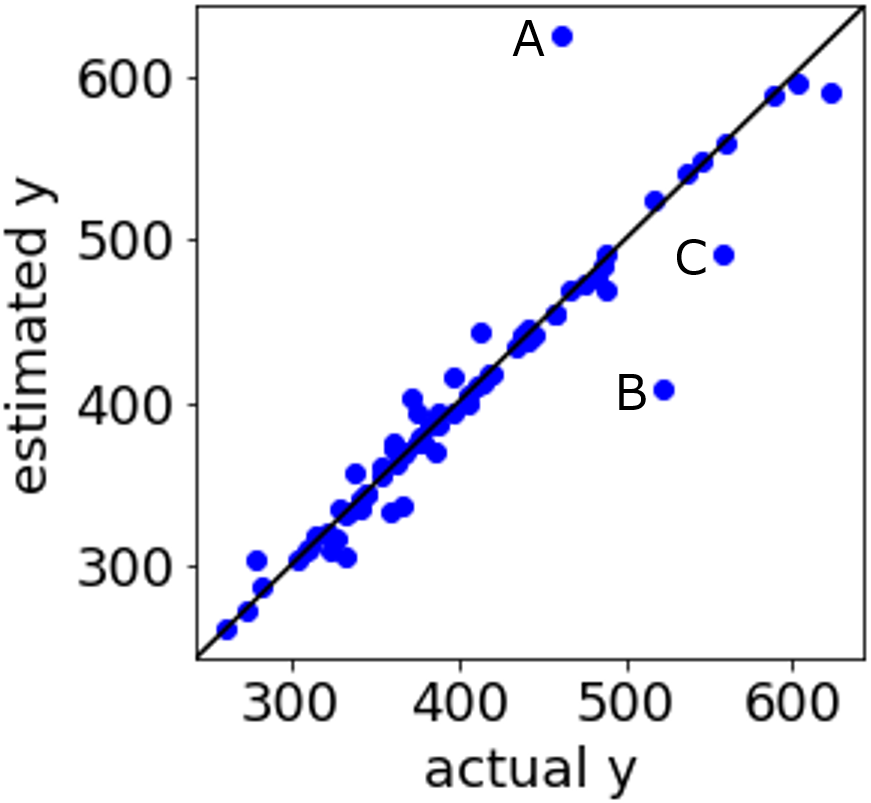
ここでの評価により、手持ちのデータセットと対象とする y に適した回帰分析手法が選択されることになります。この手法を使って最終的に用いるモデルを構築します。ここで運用するモデルを評価する方法が
- y-randomization による検証
- MAECCE
です。そもそも MAECCE は、y-randomization に基づいて計算されます。

y-randomization により、最終的に構築されたモデルに偶然の相関がどの程度影響しているのか検討できます。またそれを具体的な MAE の形で示したのが MAECCE であり、MAECCE は分布で与えられます。例えばモデルの適用範囲 (Applicability Domain) 内のデータセットが与えられたときに、誤差の平均としてどの程度の分布で予測できるか検討できます。
以上のように、回帰モデルを実際に運用するまでの流れにそって、それぞれの評価方法を整理しました。ご参考になれば幸いです。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。