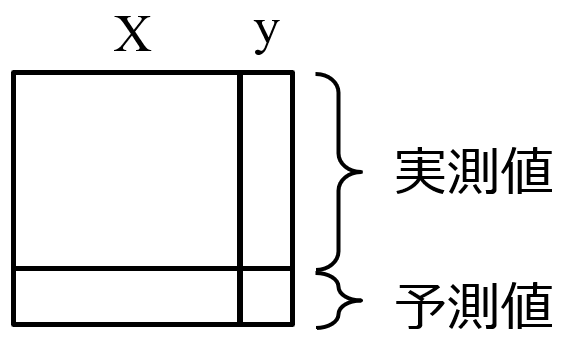
分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築し、構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。
特にモデルによる x の設計と実験・製造を繰り返す適応的実験計画法、もしくは能動学習において、ベイズ最適化が活用されます。

一般的には x の仮想サンプルを大量に生成し、ガウス過程回帰モデルで y の予測値 (正確には y の予測結果の平均ですが、ここでは分かりやすさを優先して予測値とします) とその分散を計算し、それらに基づいて獲得関数を計算し、獲得関数の値が大きい x の候補を選択します。一度に複数の実験ができたり、実験とガウス過程回帰モデルに基づく x の設計を繰り返したりする際、x の候補の多様性も重要になります。多様性が小さい、すなわち同じような x の候補ばかり実験してしまうと、ガウス過程回帰モデルの適用範囲が広がりません。
多様性を検討するために、獲得関数の種類を変えて x の候補を選択したり、ガウス過程回帰モデルのカーネル関数を変えて獲得関数を計算したり、y の予測値を実測値と仮定して逐次的に x を選択したり、ある程度獲得関数の値が大きい候補からばらつきが大きくなるように選択したりします。

いろいろなやり方はありますが、一度基本に立ち返ってみると、例えば y の実測値が大きくなるようなサンプルが目標のとき、もちろん y の予測値が大きい方が望ましいですが、y の値が同じくらい大きい場合には、ベイズ最適化を用いるということは基本的に y の目標値が非常に大きい (yの目標値が y の予測値から遠い) ケースであることから、予測値の分散が大きい方が x の候補として望ましいです。逆に分散が小さく、極端なことを言えば分散=0のときには予測値=実測値となるので、目標に全く到達できません。y の予測値が同じような候補があるときには、なるべく予測値の分散が大きい方が目標値に到達する可能性が高いと言えます。
一方で、y の予測値の分散が同じくらいの値を持つ候補であれば、もちろん y の予測値が大きい方が y の目標に到達しやすいと考えられます。
以上のことから、基本的にベイズ最適化では y の予測値とその分散 (もしくは標準偏差) とのパレート最適解が x の候補として望ましいと言えます。y の値が大きい方が望ましいとき、パレート最適解は下の図のようなイメージです。
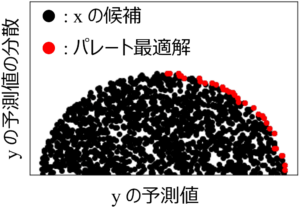
y の値が小さい方が望ましいときは、パレート最適解は以下の図のようなイメージです。

ちなみに、獲得関数で x の候補を選択することは、パレート最適解から “妥当そうな” 候補を選択していると言い換えることができます。
ベイズ最適化で次の x の候補を選択する場合や、x の多様性を考慮したい場合には、上の図のような y の予測値とその分散 (もしくは標準偏差) のプロットを確認し、次に実験する x の候補がどの位置かを確認すると良いでしょう。また、上の赤点のようなパレート最適解を確認し、そのパレート最適解の中から、例えば獲得関数が大きいような候補を選んだり、ランダムに選んだりして、x の多様性も考慮しながら選択すると良いでしょう。
y が複数あるときには、(y の数) × 2 の軸ができるので、y の数だけ図を作成する必要がありますが、それらの図の中でパレート最適解を赤点で示すことで、次に実験する x の候補を選択する見通しが立ちやすくなるでしょう。ベイズ最適化のときには、y の予測値とその分散 (もしくは標準偏差) のプロットを確認することをオススメします。
以上です。
質問やコメントなどありましたら、X, facebook, メールなどでご連絡いただけるとうれしいです。