分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築し、構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。
モデルを構築するためのサンプルが混合物であり、x として原料の種類や割合を最適化したり設計したりするとき、一般的には原料の種類ごとの組成を x とします。ただ、この x では、新しい原料を用いたときに y がどのような値になるかを予測することができません。原料の種類が x になるため、新しい原料は新しい x に対応し、モデル構築用のデータセットから x が変わってしまうためです。
では、新しい種類の原料を予測するときのように、外挿を予測して探索するためには、x をどのようにすればよいのでしょうか。考え方はこちらに記載した通りですが、

ここでは、具体的な計算手順を説明します。
モデル構築用のデータセット
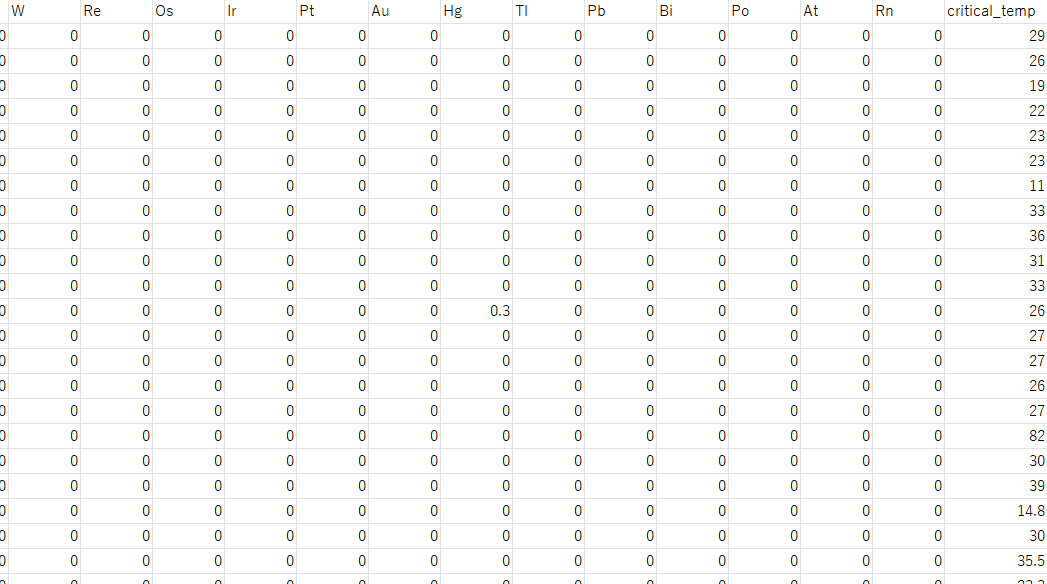
① 原料ごとの組成を準備します。例えば、下の本のサンプルデータセットでもある超伝導体材料のデータセットのように、種類ごとの組成を準備します。
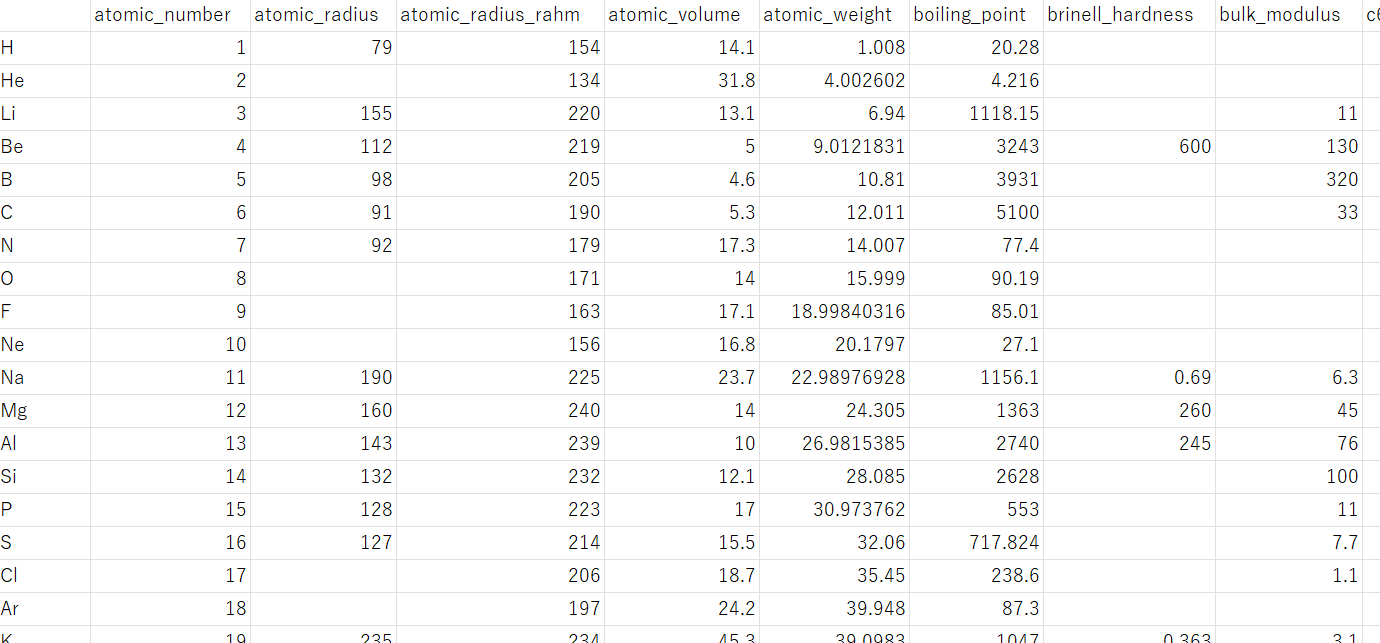
② 原料ごとの特徴量を準備します。上の超伝導体材料のデータセットあれば、以下のような元素ごとの特徴量を準備することになります。
③ 上の原料ごとの組成と特徴量に基づいて、混合物の x として数値変換します。例えば、以下のような数値変換があります。
- 加重平均 (weighted average)
- 加重分散 (weighted variance)
- 幾何平均 (geometric mean)
- 調和平均 (harmonic mean)
- 最大値 (max-pooling)
- 最小値 (min-pooling)
どの変換方法もしくは変換方法の組み合わせが適しているかは、データセットに依存します。モデル構築と評価を行う中で、試行錯誤する必要があります。
場合によっては、上記で数値変換された特徴量に、実験条件 (反応温度や反応時間など) を x に追加し、y との間で数理モデルを構築します。
予測用データセット
基本的な計算手順は、上のモデル構築用データセットの手順①②③と同じですが、②で特等量を準備できるのであれば、①において新たな原料を用いることができます。モデル構築用のデータセットの①にない列を追記できるわけです。そして②で、準備したすべての原料において、その特徴量を計算します。その後、モデル構築用データセットの③と同様に数値変換します。場合によっては、他の実験条件も x に追加します。そして、モデルに x を入力して y を 予測します。
以上のように、原料の特徴量と組成から混合物 (サンプル) の特徴量を計算することで、外挿の予測、すなわち新たな原料に対する予測が可能になります。
なお、Datachemical LAB を用いれば、上のすべての計算ができます。

ぜひご検討ください。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。