Datachemical LABで混合物の特徴量化ができるようになりました

いつも Datachemical LAB をご利用いただきありがとうございます。

これまでご紹介させていただいた通り、Datachemical LAB を使用することで、データの前処理・データの可視化・回帰分析・モデルの逆解析・モデルの適用範囲・化学構造生成・(適応的)実験計画法・能動学習・ベイズ最適化・ソフトセンサー・異常検出・直接的逆解析・クラス分類などの、データ解析・機械学習が可能になります。

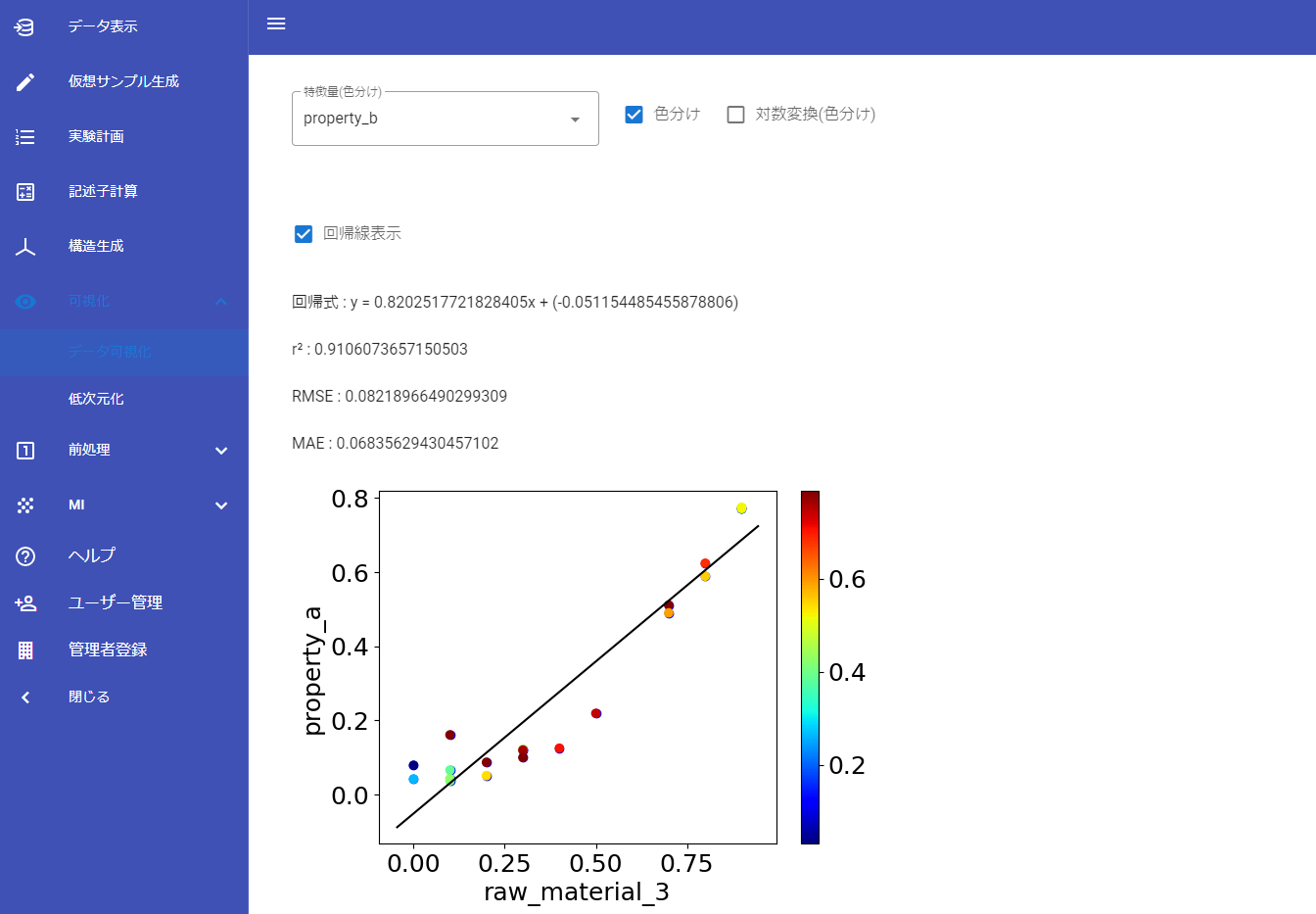
化学・化学工学分野におけるデータ解析・機械学習クラウドサービス「Datachemical LAB」

化学・化学工学分野におけるデータ解析・機械学習が、プログラミングなしでできるクラウドサービス「Datachemical LAB」を開発し、提供を開始しましたので、ご案内します。プレスリリースは以下をご覧ください。 Datachemical ...

そして、Datachemical LAB に混合物の特徴量化の機能が加わりました！プレスリリースはこちらです。

化学の研究開発AIクラウドサービス「Datachemical LAB」にて目標性能に対する材料作製条件予測のエキスパート機能をリリース https://t.co/756DE8ck5I @PRTIMES_JPより

— 金子弘昌＠「化学・化学工学のための実践データサイエンス―Pythonによるデータ解析・機械学習―」 (@hirokaneko226) December 27, 2022

Datachemical LAB のメニューの材料設計に、前処理の「混合物計算」があります。

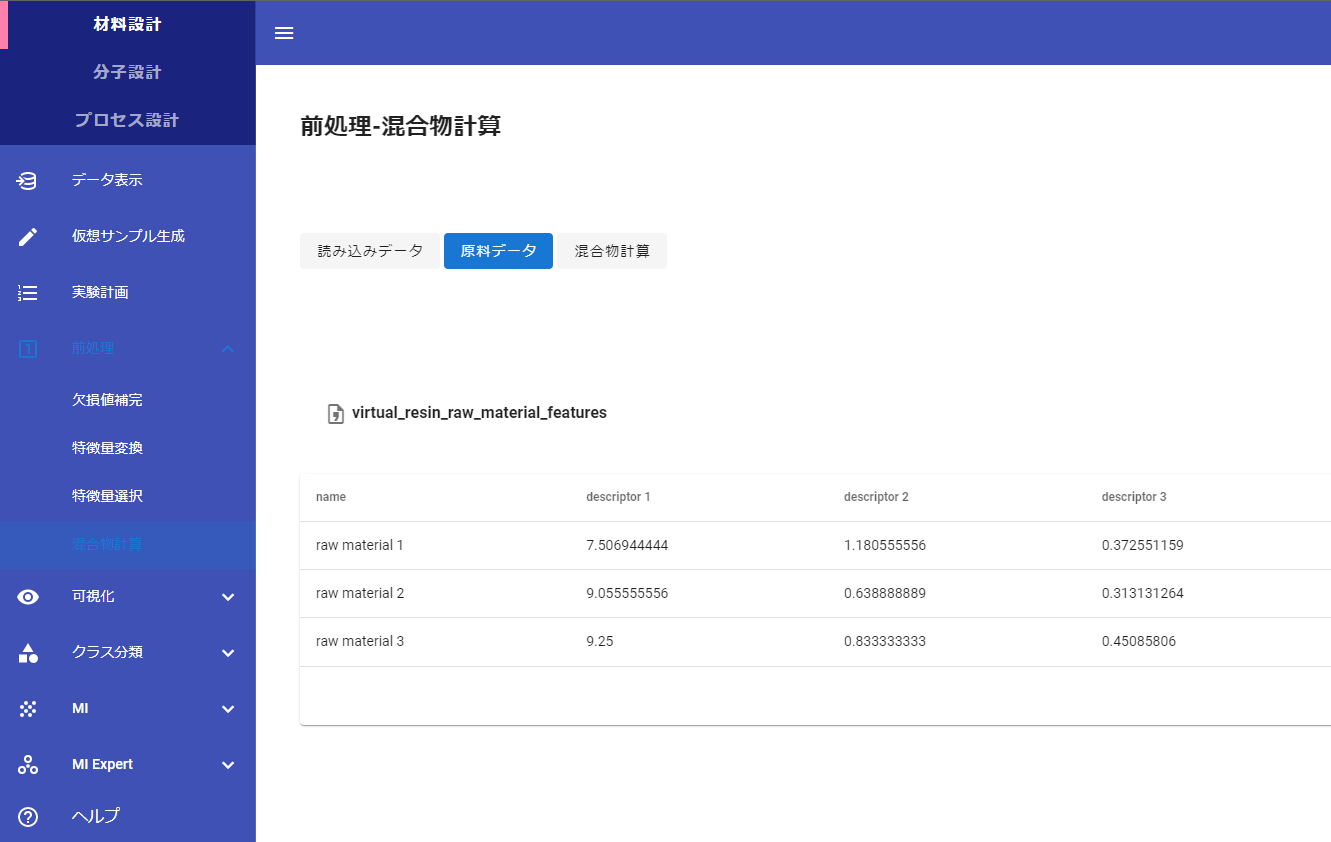
なお、Datachemical LAB のメニューが「材料設計」「分子設計」「プロセス設計」に分かれ、さらに使いやすくなりました。

分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築し、構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。

例えばポリマー設計において、共重合体 (コポリマー) の特徴量を考えるとき、各モノマーを数値化した後に、それらのモノマーの組成比を重みとした重みつき平均 (加重算術平均もしくは単に加重平均) を計算することで数値化することがあります。また合金の特徴量を考えるとき、用いる金属元素もしくは非金属元素を数値化した後に、それらの組成比を重みとした加重平均を計算することで数値化します。他にも、複数の物質を混合して材料を作る場合など、一般的に混合物の特徴量を考えるとき、各物質の組成比を重みとした加重平均によって、対象の材料を数値化することが行われます。

これは適当に加重平均を計算しているわけではありません。特徴量を作成するとき、混合物をどのように数値化するか、と考えます。非常に単純な例ですが、化学構造を置換基の数で数値化するとき、複数の化合物を混ぜた後の置換基の数は、それぞれの化合物の置換基の数に、混合した量 (物質量) を掛け合わせて、すべて足し合わせたものといえます。加重平均の考え方です。もちろん、それらの化合物間の関係 (水素結合など) については考慮できませんが、それぞれの化合物が独立に存在すると仮定したときに数値化していると考えることはできます。原子量・分子量・式量に関しても、置換基と同じ考え方ができます。

もちろん、複雑な構造記述子や金属元素もしくは非金属元素の情報において、加重平均を計算してよいのか、と考える場合もありますが、上で示した考え方を拡張して、加重平均で数値化します。また物質の特徴量によっては、重みをつけて算術平均を計算するのではなく、重みでべき乗して幾何平均を計算する (加重幾何平均を計算する) 方が適切なこともあります。なお加重幾何平均については、対数変換をすると、各特徴量を対数変換した後に加重平均を計算したものに対応しますので、そちらの方が変換しやすいかもしれません。他にも、加重分散、調和平均、max-pooling, min-pooling といった変換方法があります。

混合物を数値化するときには、単純に加重平均を取るだけでなく、どのようにして混合物を数値化して特徴量とすれば、特徴量と活性・物性・特性との間の関係性を得られやすいか、といった視点で考えるとよいでしょう。

Datachemical LAB には、純物質の特徴量と組成比に基づいて、以下の６通りの方法で混合物の特徴量を計算することが可能です。