回帰モデルやクラス分類モデルを構築したあとの、モデルの逆解析についてです。

こちらのチェックリストを確認したあとの話ですね。

モデルの逆解析のとき、目的変数が一つでしたら、その推定値がよさそうなサンプルを選んだり、ベイズ最適化で獲得関数の値が大きいサンプルを選んだりすれば OK です。
目的変数の数が二つ以上になると、難しくなります。目的変数ごとに目標があったり値に目標範囲があったりして、すべてを (いい感じで) 考慮したサンプルを選ぶ必要があるためです。このあたりのサンプルの選び方について話します。
ベイズ最適化をしたいとき
ベイズ最適化をするときは、単純かもしれません。こちらに書いたように、

目的変数ごとに目標を満たす確率を計算し、それらを掛け合わせることで、すべての目的変数の目標を同時に満たす確率にします。この確率が高いサンプルを選びます。
目的変数の推定値を見てモデルの逆解析をしたい
ベイズ最適化ではなく、各目的変数の推定値を考慮して、サンプルを選びたいときもあるでしょう。

こんなとき、基本的にはそのデータ解析の目的に応じてサンプルを選ぶのがよいと思います。たとえば材料設計のとき、複数の物性 (目的変数) があり、それぞれ目標値があるといっても、優先順位があるはずです。その優先順位にしたがって、推定値のよさそうなサンプルを選ぶわけです。
ただ、たとえばサンプルが 100 万個ある、つまり推定値の候補が 100 万通りあるとすると、すべてのサンプルをチェックするのは非常に大変です。100 万候補から、チェックすべき候補を効率的に選びたいですね。
パレート最適解を選択する
一つのやり方は、サンプルの中からパレート最適解を選択する方法です。パレート最適解とは、の説明をするより、パレート最適解ではないサンプルの説明をして、それではないのがパレート最適解、としたほうがわかりやすいです。あるサンプルについて、すべての目的変数において目標に近い別のサンプルがあるとき、そのサンプルはパレート最適解ではありません。パレート最適解ではないサンプルをすべて除いたとき、残ったサンプルがパレート最適解です。パレート最適解の詳細はこちらをご覧ください。
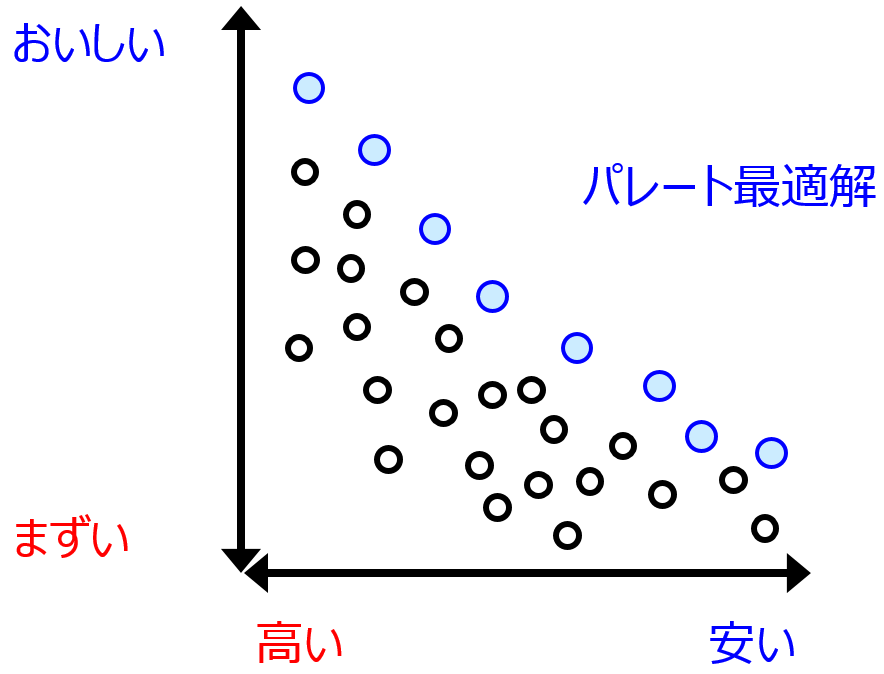
パレート最適解のサンプルのみチェックすることで、100 万サンプルすべて確認する必要がなくなります。
一つの指標に落とし込む
パレート最適解を選ぶ以外の方法の一つに、一つの指標に落とし込み、その指標に基づいてサンプルを選ぶ方法があります。ベイズ最適化において、目的変数ごとの目標値を達成する確率をすべて掛け合わせた指標のようなイメージです。確率でしたら、すべての目的変数で「確率」なので、平等に扱うことができました。ただ、推定値は目的変数ごとに目標値やばらつきが異なるため、そのままでは平等に扱えません。どのように処理したらよいでしょうか。
まず、目的変数ごとに推定値から目標値からを引いた変数にします。そしてそれを絶対値にします (値が 0 以上になります)。この変換により、0 に近いほど目標値に近くなります。さらに、変換された変数を、各目的変数の実測値の標準偏差で割ります (推定値の標準偏差ではありませんので注意してください)。すべての変数を標準化する感じです。
以上の操作により、0 に近いほど目標値に近くなり、かつすべての変数のスケールを合わせて平等に扱えるようになります。最後にすべての変数の和を取り、一つの指標とします。この指標の値が 0 に近い順にサンプルを並び替えて、順番にチェックすると効率的になるわけです。単純にすべての変数の和を取るのではなく、変数ごとに重みを付けて足し合わせてもよいかもしれません。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


