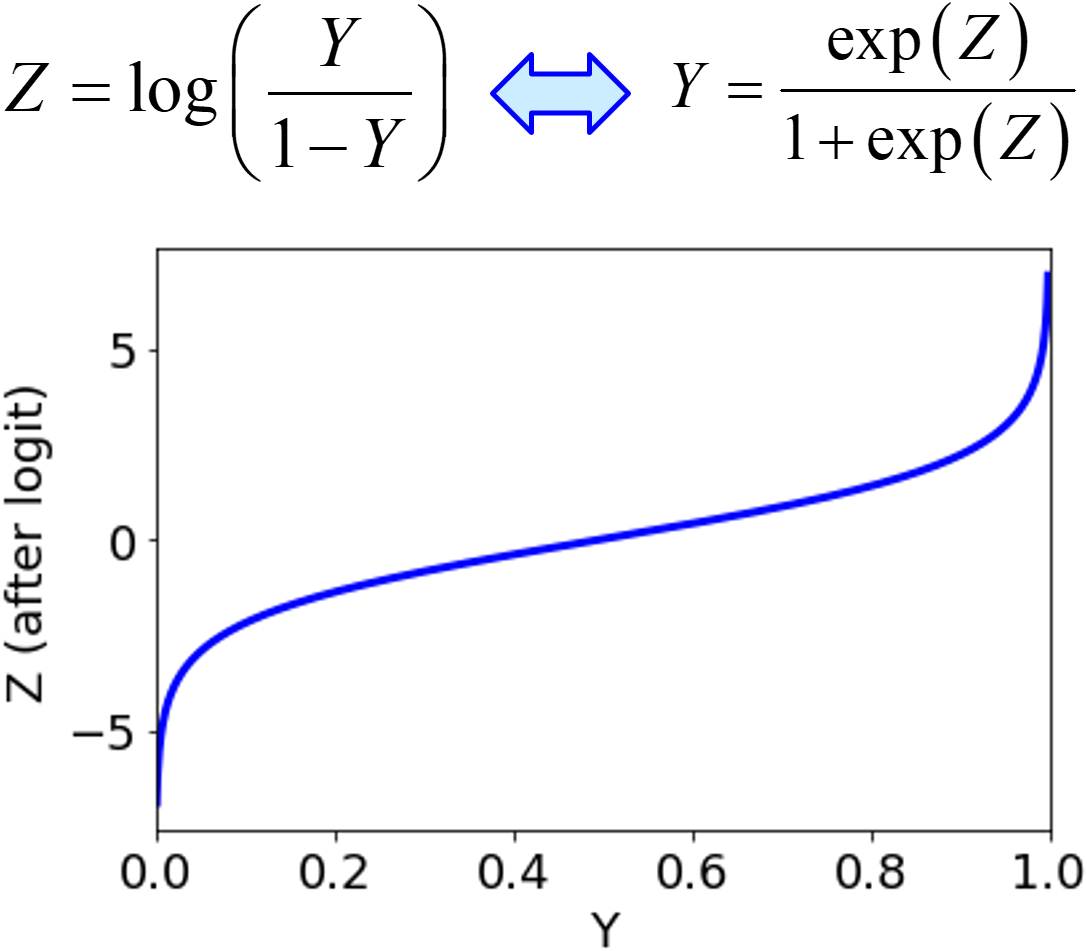
今回は、目的変数 Y の値が 0 から 1 の間にあり、回帰分析をするときの話です。例えば Y がモル分率などのときですね。このような Y と説明変数 X の間で回帰モデル Y=f(X) を構築して、X の値から Y の値を予測したとき、予測値が 0 より小さくなってしまったり、1 より大きくなってしまったりすることがあると思います。仕方がありませんので、0 より小さい値を強制的に 0 にしたり、1 より大きい値を強制的に 1 にしたりします。
このような強制的な変更が気持ち悪いとき、ロジット変換を利用できます。ロジット変換は、以下のように Y を Z にする変換です。
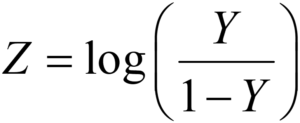
値が 0 から 1 の間の Y が、マイナス無限大 (−∞) から無限大 (∞) までの Z になります。
この Z を Y の代わりにして、X との間で回帰モデル Z=f(X) を構築します。このとき、X の値をモデルに入力して得られるのは、Z の予測値です。この Z は、逆ロジット変換することで、Y に戻すことができます。逆ロジット変換は、以下のように Z を Y にする変換です。
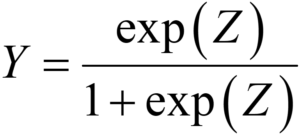
変換された Y は、必ず 0 から 1 の間になります。
ロジット変換を利用するときに注意することは、ロジット変換の式を見ると分かるよう、Y が (厳密に) 0 だったり、1 だったりするサンプルがあると、使えないということです。例えば 0 を 0.001 に、1 を 0.999 にすることが問題ないときなど、そのようなサンプルを適切に置き換えることができれば問題ありませんが、注意しましょう。
また、ロジット変換における Y と Z の関係は下の図のようになり、
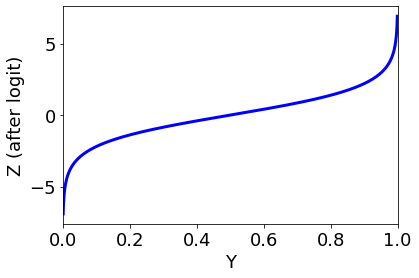
Y が 0.5 から離れるほど、Z の値の絶対値が大きくなり、誤差に対する寄与が大きくなり、その誤差が小さくなる傾向があります。Y が 0 に近いサンプルほど、もしくは 1 に近いサンプルほど、誤差が小さくなる傾向があるということです。0.5 付近を精度よく予測したいときは注意しましょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。