決定木で回帰分析やクラス分類を行うときの話です。
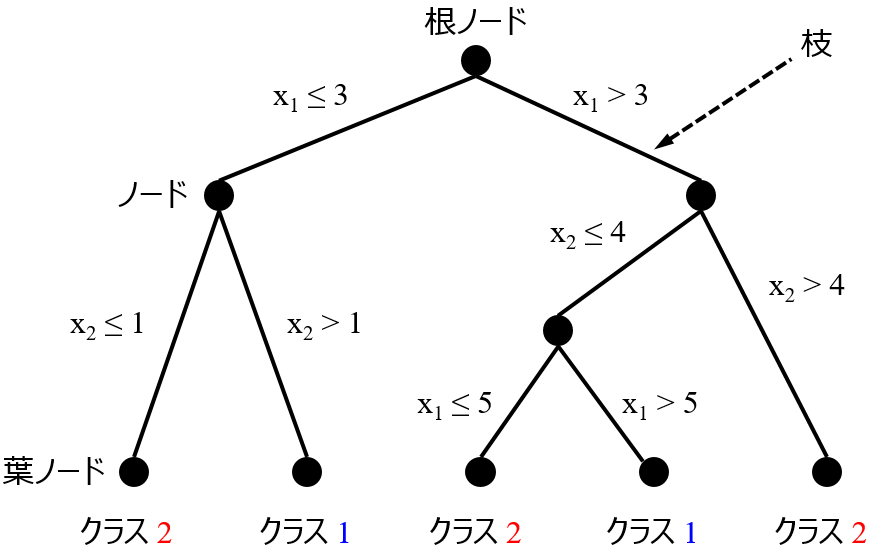
決定木では、他の手法と比べて回帰モデルやクラス分類モデルの予測精度が低くなってしまうことがあると思います。こんなとき、もう決定木は用済み、としてしまうのはもったいないかもしれません。
決定木の代わりに、例えばランダムフォレストを用いることで、モデルの予測精度が向上することが多々あります。
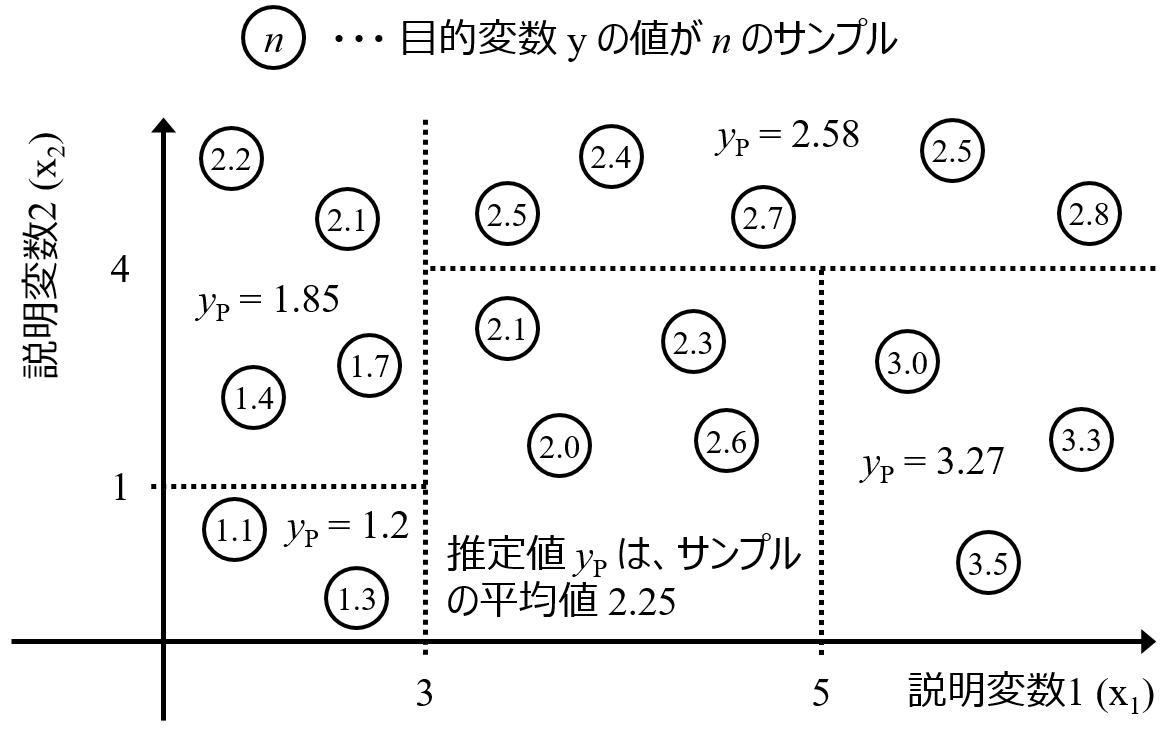
しかし、ランダムフォレストと比べて予測精度の低かった決定木にも、メリットのひとつとして、構築されたモデルを解釈しやすい、というのがあります。モデルが木のような構造で与えられるため、それを見ることで、説明変数とその閾値のいくつかの組み合わせにより、目的変数が大きくなったり、小さくなったり、ある値になったり、あるクラスになったりするときの説明変数の特徴をルールとして取り出すことができます。
ただ、決定木によって構築されたモデルの予測精度は、少なくともランダムフォレストにより構築されたモデルの予測精度より低いということですので、そのような結果のモデルを解釈することに意味があるのか?と考えると思います。
こんなときには、決定木全体を解釈するのではなく、木を部分的に見て、局所的に解釈するのがよいと思います。モデル全体の予測精度は低いため、全体的なモデル解釈するのではなく、知りたいところや精度の良好な部分のみ、局所的に解釈するわけです。
例として、沸点のデータを用いて、決定木により回帰分析を行ってみます。木の深さの最大値を 3 にしてモデル構築すると、以下のような木ができました。
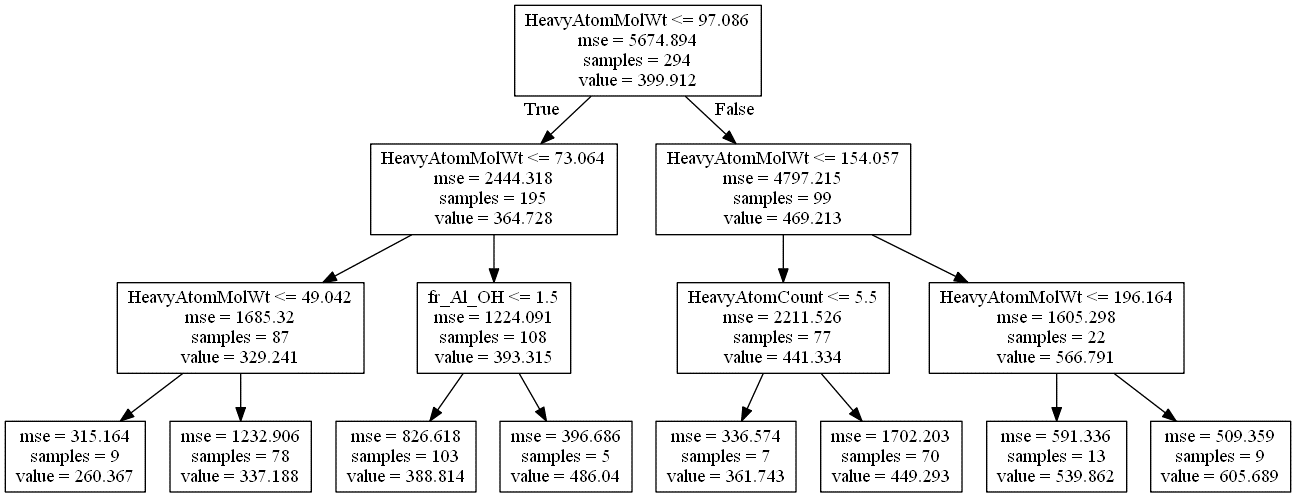
ちなみに、決定木の見方として、各四角がノードを表します。例えば下の図のノード (上の図における一番上のノードです) では、サンプル数は 294 (samples = 294)、294 サンプルにおける沸点の平均値は 399.912 (value = 399.912)、この平均値を推定値としたときの誤差の二乗の平均は 5674.894 (mse = 5674.894) であることを表します。そして、HeavyAtomMolWt (水素原子以外の原子で計算された分子量) の変数が選ばれ、その閾値が 97.086 であり (HeavyAtomMolWt <= 97.086)、97.086 以下のサンプルは左のノードへ (True)、97.086 より大きいサンプルは右のノードへ (False) 移ります。上の図において、次の 2 つのノードにおけるサンプル数を足すと、294 になることがわかります。他のノードの見方も同様です。

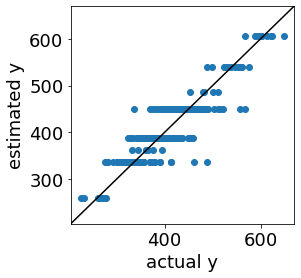
このように決定木では説明変数とその閾値のルールが得られますが、実測値 vs. 推定値プロットは以下のようであり、推定誤差の大きいサンプルもあることがわかります。
そこで決定木のモデルを局所的に見ます。下の図のような感じです。
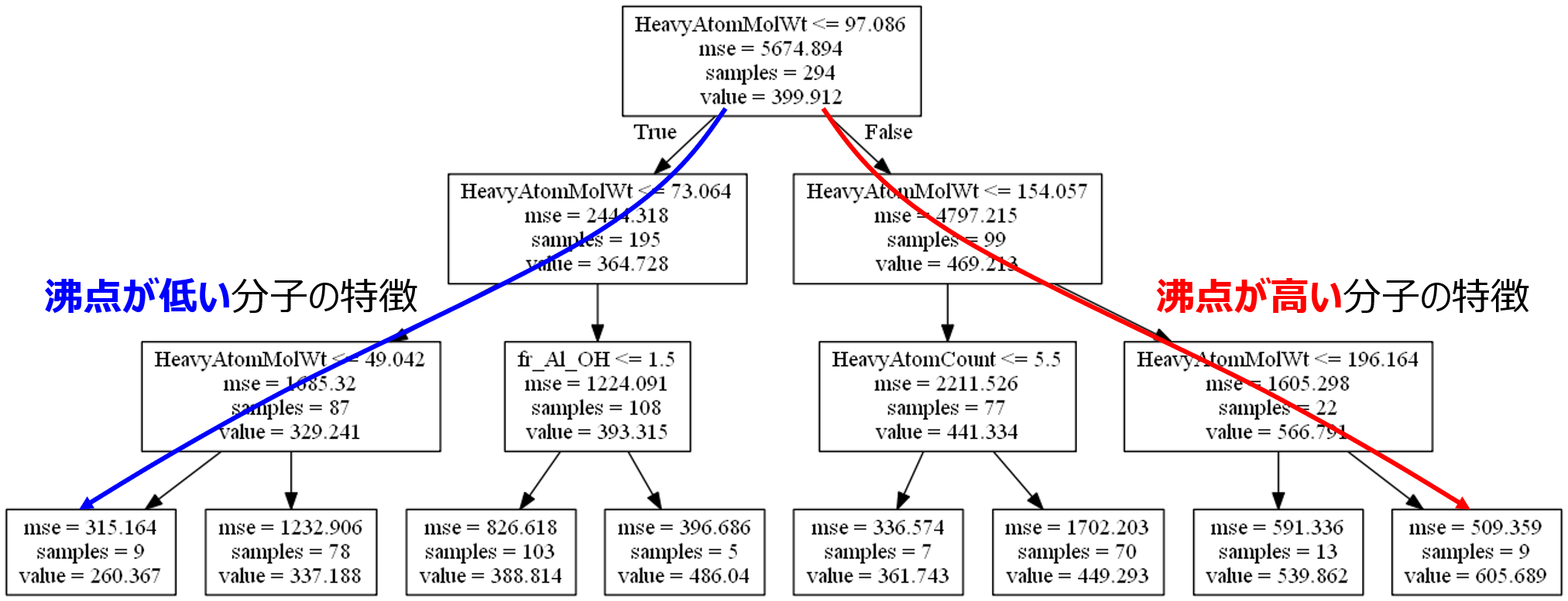
右下のノード (赤矢印の先のノード) では、沸点の平均値が 605.689 とノードの中で最大であることがわかります。サンプル数は 9 と少ないですが、このノードに来るまでの説明変数と閾値のルールを追うことで、沸点が高い分子の特徴がわかります。なお、一番下のノードまで行かず、その上のノードまでのルールにすると、沸点の平均値は 566.791 と小さくなりますが、サンプル数は 22 と増え、より一般的なルールになります。
左下のノード (青矢印の先のノード) では、沸点の平均値が 260.367 とノードの中で最小であることがわかります。サンプル数は 9 と少ないですが、このノードに来るまでの説明変数と閾値のルールを追うことで、沸点が低い分子の特徴がわかります。なお、一番下のノードまで行かず、その上のノードまでのルールにすると、沸点の平均値は 329.241 と大きくなりますが、サンプル数は 87 と増え、より一般的なルールになります。
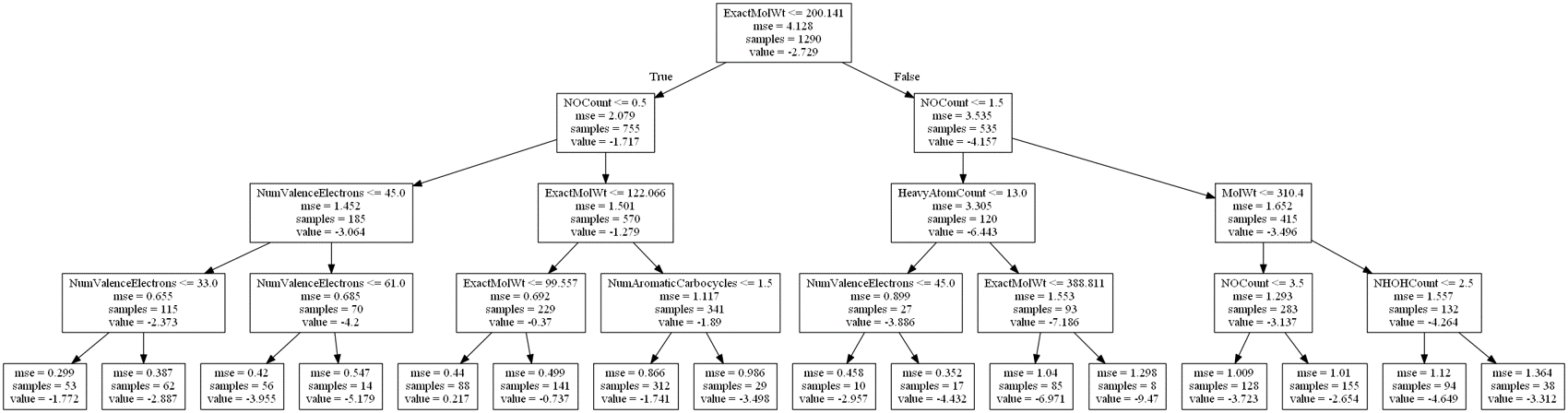
続いて、水溶解度のデータ (目的変数は水への溶解度 S の対数値 logS) を用いて、決定木により回帰分析を行ってみます。木の深さの最大値を 4 にしてモデル構築すると、以下のような木ができました。
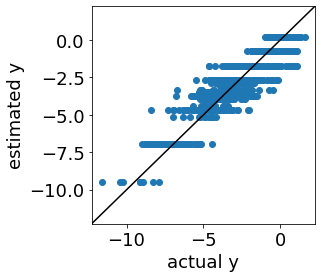
ただ、実測値 vs. 推定値プロットは以下のようであり、推定誤差の大きいサンプルもあることがわかります。
そこで決定木のモデルを局所的に見ます。下の図のような感じです。
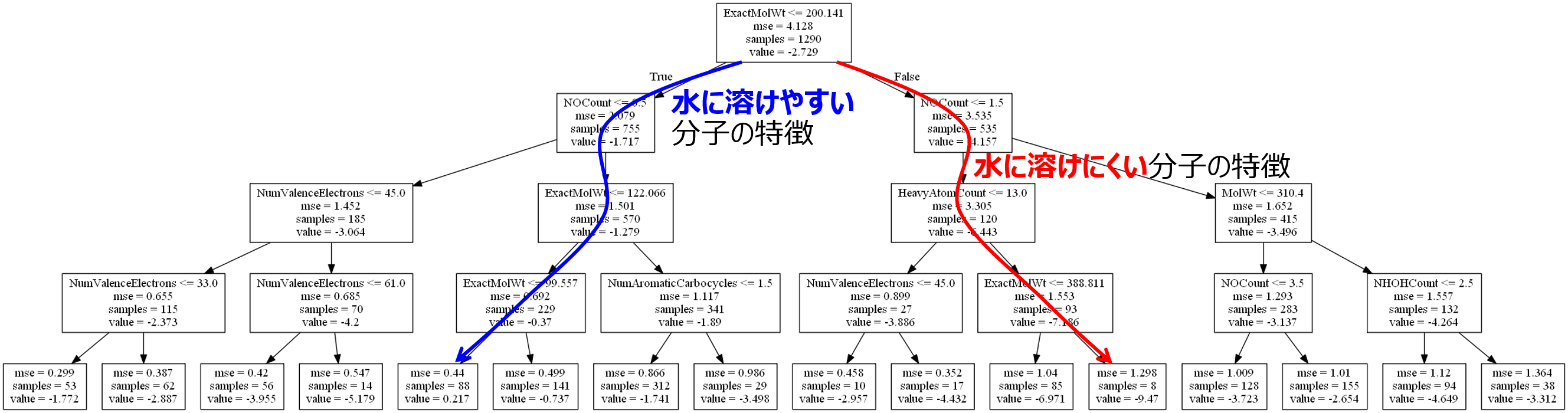
青矢印の先のノードでは、logS の平均値が 0.217 とノードの中で最大であることがわかります。サンプル数は 88 とある程度多いです。このノードに来るまでの説明変数と閾値のルールを追うことで、水に溶けやすい分子の特徴がわかります。なお、一番下のノードまで行かず、その上のノードまでのルールにすると、logS の平均値は −0.37 と小さくなりますが、サンプル数は 229 と増え、より一般的なルールになります。
赤矢印の先のノードでは、logS の平均値が −9.47 とノードの中で最小であることがわかります。サンプル数は 8 と少ないですが、このノードに来るまでの説明変数と閾値のルールを追うことで、水に溶けにくい分子の特徴がわかります。なお、一番下のノードまで行かず、その上のノードまでのルールにすると、logS の平均値は −7.186 と大きくなりますが、サンプル数は 93 と増え、より一般的なルールになります。
今回は回帰分析において、目的変数の値が大きくなるときの説明変数の特徴、小さくなるときの説明変数の特徴についてお話しましたが、もちろん目的変数の値がある値付近になるときの説明変数の特徴や、クラス分類においてあるクラスになるときの説明変数の特徴などでも、局所的に議論することができます。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


