回帰分析をするとき、目的変数 y に上限や下限のある変数を使用するときがあります。0 から 1 までの値だったり、0 % から 100 % までの間だったりする変数です。基本的には、回帰分析における y として使用して問題ありません。ただ、このような y の中には、例えば人が評価したような結果として、0 を下限、100 を上限のように決めている、もしくは丸め込んでいる場合もあります。そのようなとき、y が連続値とはいえ、回帰分析をおこなうと潜在的に問題があります。モデルの予測精度の低下にもつながりますので、把握しておくとよいでしょう。
問題は、例えば y の値が 100 であるサンプルが複数あるとき、まさに 100 のサンプルもあれば、本来であれば100 以上であったりその可能性があったりするにもかかわらず 100 としているようなサンプルもある、ということに由来します。逆にいえば、このような状況になり得るような y を扱う場合は、回帰分析をすると潜在的に問題があります。本来は y が 100 以上となるサンプルに対する真値が 100 となるため、説明変数 x から 100 と計算できるようなモデルのパラメータを設定できても、そのパラメータは間違いということになります。このサンプルには潜在的な誤差があることになり、この誤差がモデルに考慮されず、本来の y と x の間の関係を構築できません。モデル構築時にはこのような問題があることを把握しておくとよいと思います。
このようなときの一つの対処法として、完璧に解決できるわけではありませんが、ロジット変換があります。
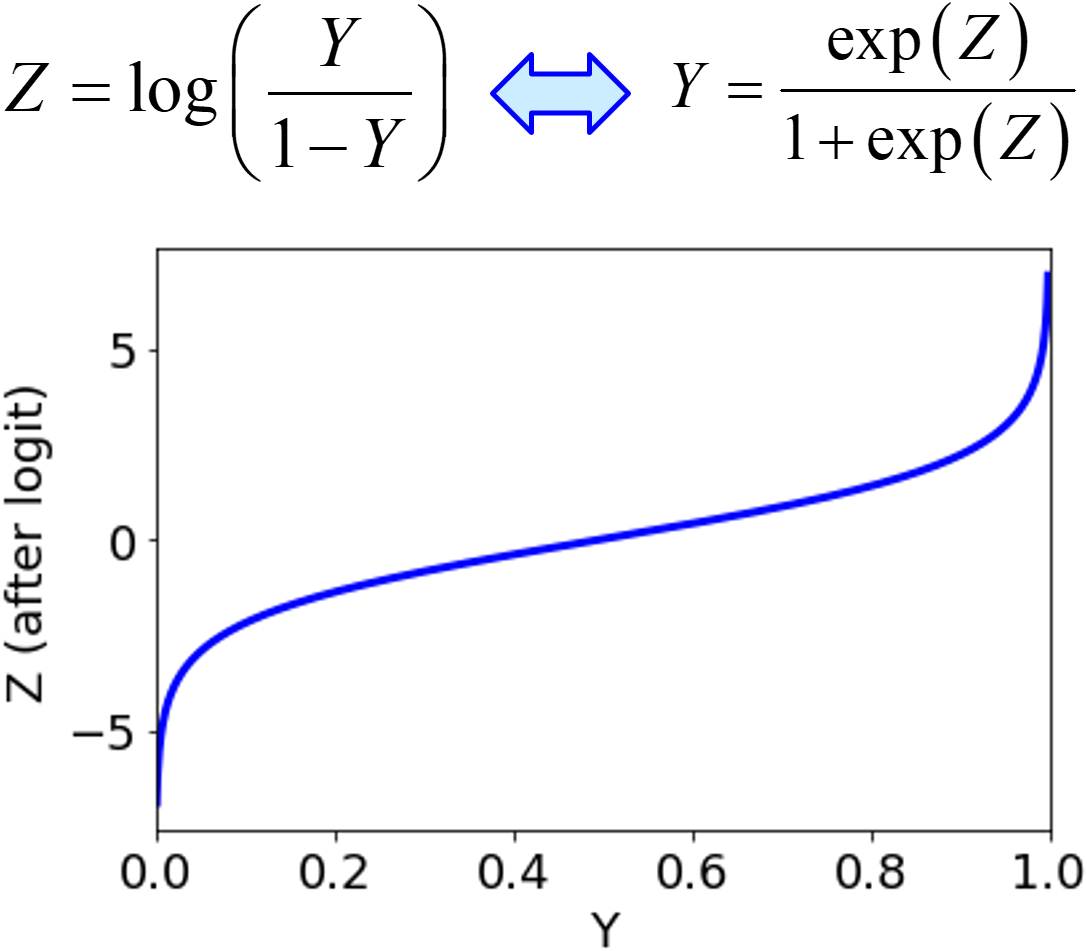
ロジット変換によって、実質的に y がマイナス無限大から無限大までに変換されるため、y を上手く設定することで y の誤差を適切に評価できる可能性があります。ただ元の y の値が 100 で同じであれば、ロジット変換した後も同じ値になりますので、この場合の根本的な解決にはなりません。
根本的な対処法としては、上手くしきい値を設けて、クラス分類するとよいです。例えば、50 未満のサンプルと 50 以上のサンプルに分けて 2 クラスにしてクラス分類モデルを構築します。しきい値や何クラスにするかは工夫する必要があります。回帰分析 → クラス分類にすることで上の潜在的な問題は解消されます。実際に、このような y を扱う状況で回帰分析からクラス分類することで、モデルの精度が向上したケースもありました。
ちなみに、基本的にクラス分類は、50 未満のクラスか 50 以上のクラスか、といった 0, 1 で分類する方法になりますが、うまく工夫することで 50 以上のクラスの中でも 100 に近い (50から離れている) か 50 に近いかを計算できます。例えばサポートベクターマシンにおける識別面からの距離や、ランダムフォレストなどのアンサンブル学習における各サブモデルで推定されたクラスの割合です。
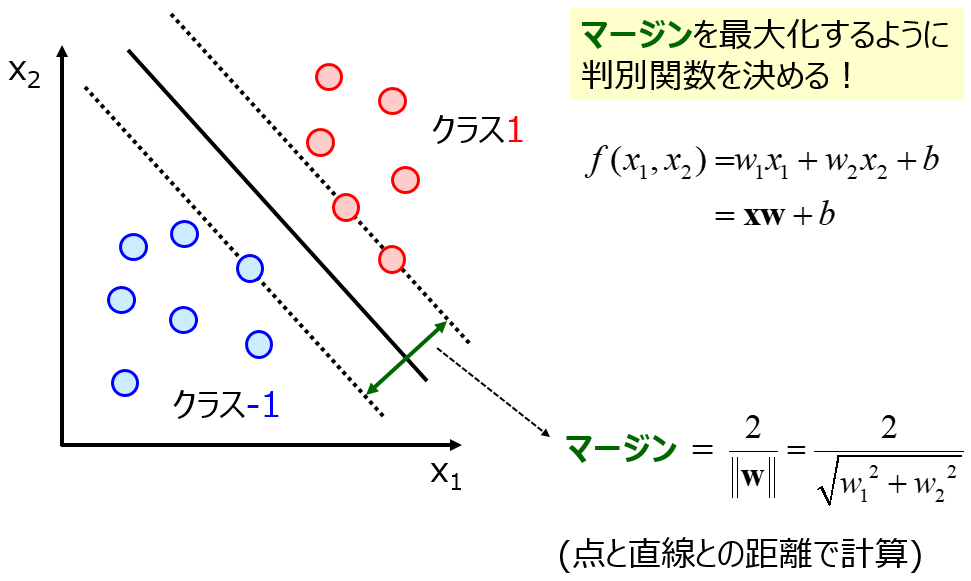
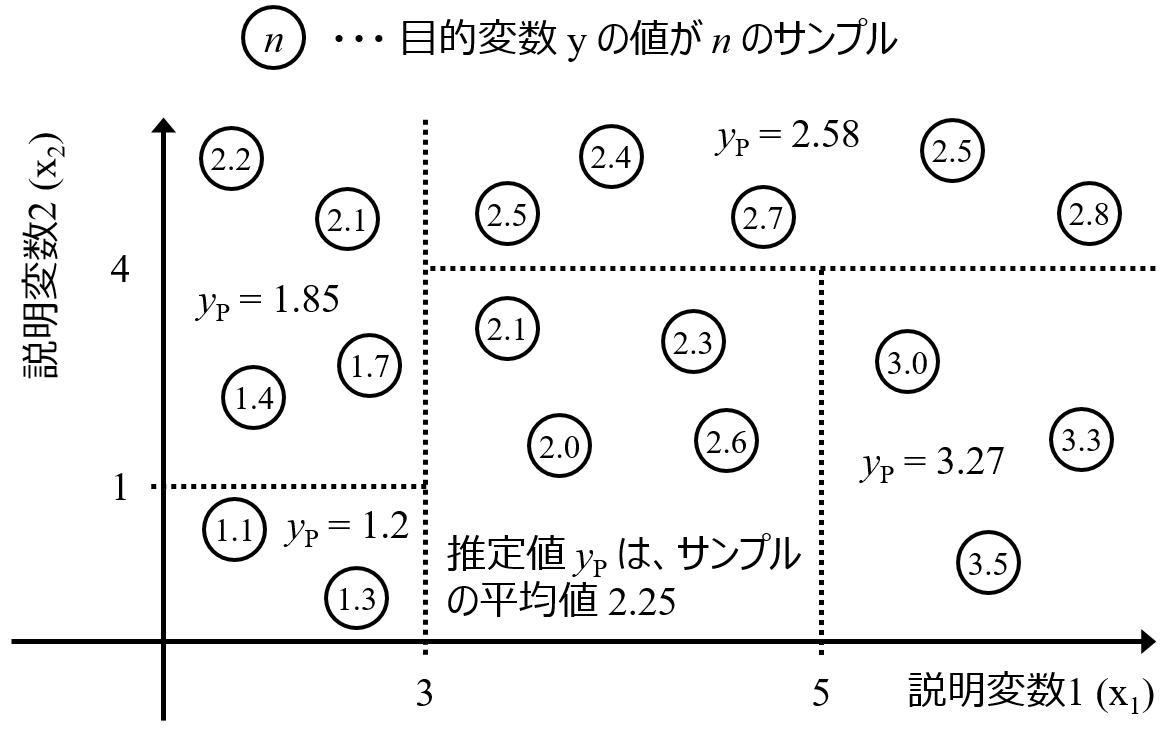
以上のように、回帰分析において上限や下限のある y を扱うときは、クラス分類の問題にして対応するのがよいでしょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


