データ解析や機械学習を活用した研究・開発において、予測精度の高いモデルが作れなかったり、モデルの逆解析で有望そうなサンプルが得られなかったりして、困ったり壁を感じたりしたときの話です。
一般的にはその状況を打破するような新たな手法や戦略を探したり、調べたり、考えたりすることになると思います。もちろん、何か高度な手法を使うことで状況が改善することもあります。ただ一方で、すべての問題に対して、問題に対して適切で高度な手法が存在しているわけではありません。そもそも問題を明確にすることが難しいこともあります。
そんなとき、基本・基礎に立ち戻ることも重要です。サンプル一つ一つを確認してそれぞれの結果が得られた実験を再度調べたり、特徴量をもう一度精査してそれぞれの意味を考えたり、使用した回帰分析手法やクラス分類手法の内容を復習したり、モデルの逆解析で得られたサンプルの内容を確認したりすることが大事です。
その意味で、データ解析や機械学習のいろいろな手法や戦略については、アルゴリズムまで (復習して) 理解することが重要です。アルゴリズムを理解することにより、例えば予測精度を向上させるような次の一手を打ち出せる可能性があります。
例えば、回帰分析においてモデリングするときに最適化するパラメータの数について、サポートベクター回帰 (Support Vector Regression, SVR) ではサンプルの数に依存する一方で、Gaussian Mixture Regression (GMR) では説明変数の数に依存することがわかります。

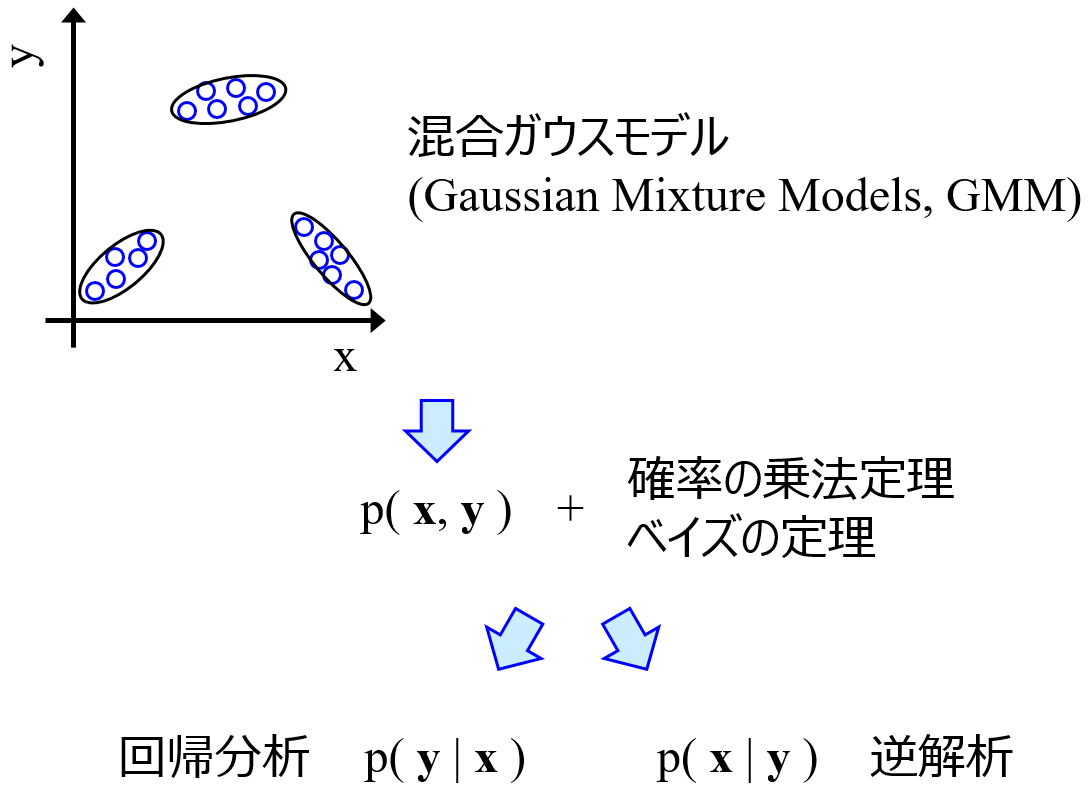
もちろん SVR では C や ε の値によっても変わりますし、GMR では正規分布の数や分散共分散行列の種類によっても変わりますが、SVR ではサンプルの数が大きいほど、GMR では説明変数の数が大きいほど、最適化するパラメータの数が大きい傾向があります。
パラメータの数が大きいほど、トレーニングデータのサンプルを説明する能力が上がりますが、大きすぎると、最適化が困難になったりオーバーフィッティングの危険が増えたりします。SVR と GMR について理解することで、パラメータの数を調整するために立てられる戦略は SVR と GMR で異なることがわかります。
例えば GMR では説明変数の数が多いとパラメータを最適化することは困難ということですので、潜在変数として低減してからモデリングをする、といった戦略も考えられます。
以上のように、各手法のアルゴリズムまで立ち戻ることで、データ解析や機械学習において問題があるときでも、次の一手を打ち出せる可能性があります。基礎に立ち戻るとき、特にデータ解析や機械学習の手法は難しいものも多いですが、頑張って理解することで、道は開ける可能性があります。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


