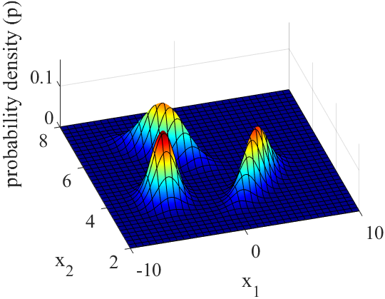
説明変数 x と目的変数 y の間のモデル y = f(x) について、モデルの予測精度を向上させようとするとき、x の特徴量の検討は非常に重要です。データ収集のときに適切な特徴量のデータを集めたり、データ収集後に特徴量を適切に変換したりすることで、モデルの予測精度を向上させる可能性があります。もちろん、モデル検討のときに、どの特徴量が y と関係していたり重要であったりするのかのすべての判断ができるわけではありません。そのため、ある程度多くの特徴量のデータを収集することになるかと思います。
このときに注意することとしては、モデルを構築し、構築したモデルの解釈をする、すなわち特徴量の重要度や x の y に対する影響を検討する際、不要な特徴量があることよりも、重要な特徴量がないことの方が問題になります。重要な特徴量がないとき、ない特徴量の分だけ予測精度が下がったり、解釈が曖昧になったりする以上の問題があります。
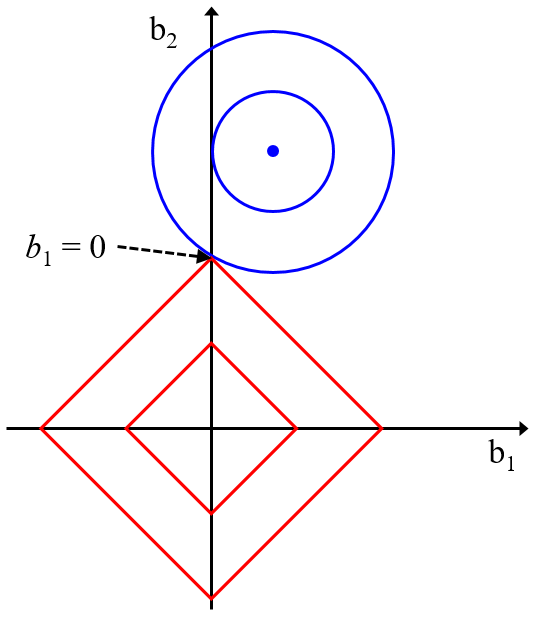
いろいろな回帰分析手法がありますが、多くの手法はデータセットの中にノイズがあっても良好な予測精度になるように開発されてきました。そのため、もちろん不要な特徴量がないことに越したことはありませんが、もし不要な特徴量が x にあっても、ある程度は手法の方で対処できます。例えば LASSO では回帰係数が 0 になり、対応する特徴量が使用されない仕組みがありますし、
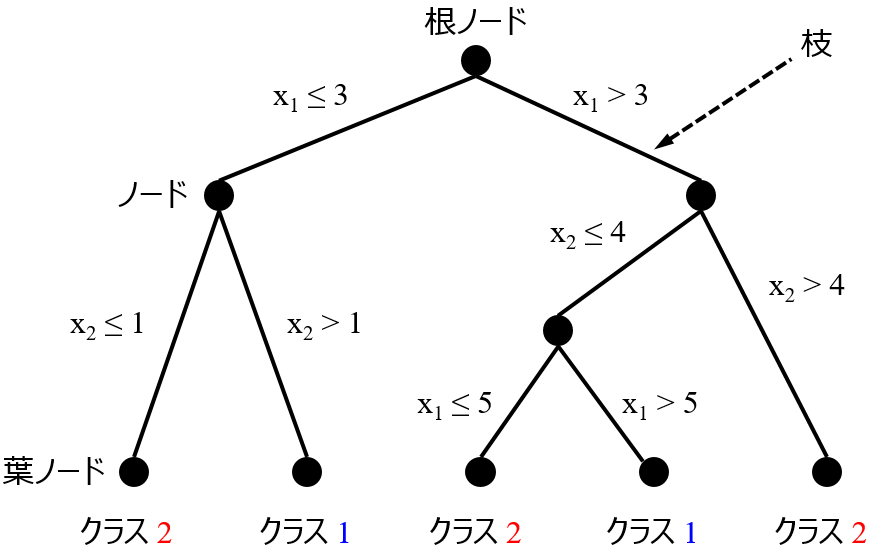
決定木でも、x においてモデル構築に使われない特徴料があることもあります。
一方で、y と関係のある特徴量が本来はあるにもかかわらず、データセットに含まれていないと、誤った形でモデルが構築されてしまう可能性があります。基本的に回帰分析手法は、ノイズに対応しながらも、y の実測値と予測値との差がなるべく小さくなるように、モデルが構築されます。y と関係している重要な特徴量が x にあれば、その関係性を再現するように、その特徴量で y を説明するようにモデルが構築されます。しかし、そのような特徴量がないときには、もしかしたらノイズかもしれない他の特徴量の変動で、y を説明しようとしてしまいます。ここで得られたモデルは、本来の関係ではありませんので、モデルが過学習してしまったり、重要度が誤った数値として出てきたりしてしまい、誤った解釈を導いてしまうこともあります。データ収集の際にたくさんの特徴量のデータを集めることは大変な作業とは思いますが、誤った結論を導かないようにするためにも、最初にしっかりとデータ収集をしておくことが重要といえます。y と関係があると少しでも考えられる特徴量は、使用できるよう準備するとよいでしょう。
ちなみに、モデルの予測性能を向上させようと x を選択するタイプの特徴量選択手法を用いることも、同じ理由、すなわち重要な特徴量が省かれてしまう危険があるという点で、注意する必要があります。そのような特徴量選択手法では、モデルの予測精度と向上させるとはいっても、基本的にはクロスバリデーション等の内部バリデーションで評価した精度であるため、その指標に過学習した、本質的ではない特徴量が選択されてしまい、重要な特徴量が除かれてしまう危険があります。そのため、モデルの予測精度を向上させようと特徴量選択するときは注意するとよいでしょう。
モデルの予測精度とは関係なく、例えば特徴量間の相関係数の絶対値で特徴量を削除する場合は、ある程度相関係数の絶対値の閾値を大きくすることで、重要な特徴量が除かれてしまう危険は小さいといえます。もちろん、相関係数の絶対値の大きい組の、どちらが意味のある特徴量かは考える必要があります。ただ、どちらにせよ類似した特徴量のどちらかが x に含まれるため、モデルの予測精度の観点からは問題ないと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。