金子研の論文が Chemometrics and Intelligent Laboratory Systems に掲載されましたので、ご紹介します。タイトルは
です。これは修士卒の山田 信仁さんが修士のときに取り組んだ研究の成果です。
適応型ソフトセンサー (adaptive soft sensor) の予測精度を向上させる一つの取り組みとして、プロセス変数 x の選択があります。重要な x のみ選択することで、目的変数 y と関係のない x がノイズとなって適応型ソフトセンサーに影響することを防ぐことができ、予測精度の向上につながります。
また、プロセスの動特性、すなわち x がどれくらいの時間遅れをともなって y に影響しているかを考慮することも重要です。x の時間遅れを的確に考慮できれば、それ以外の時間がノイズとなって y に影響することを防ぐことができ、予測精度の向上につながります。
一方で、重要な x やその時間遅れは、プロセス状態ごとに異なると考えられます。たとえば異なる銘柄の製品を製造するプラントにおいて、銘柄ごとに異なる x や時間遅れが重要となる可能性があります。ただ、これまでは適応型ソフトセンサーを開発しようとしたとき、収集したデータセットをすべて用いて x やその時間遅れを最適化して得られた、一セットの x とその時間遅れを使用しておりました。同じデータセットの中でも、重要な x やその時間遅れはプロセス状態ごとに異なると考えられます。
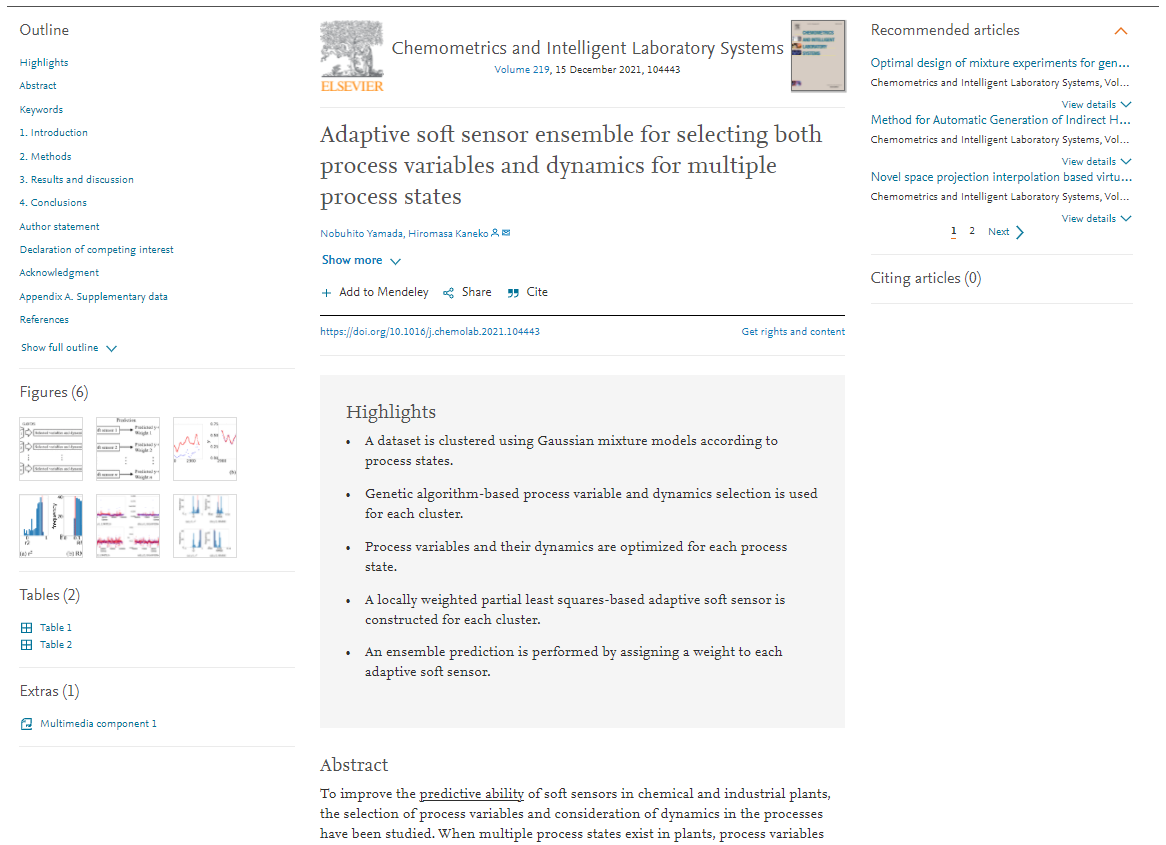
そこで提案手法ではまず、Gaussian Mixture Model (GMM) でクラスタリングを行い、データセットをプロセス状態ごとに分割します。
Bayesian Information Criterion (BIC) を指標にすることでクラスターの数も自動的に決定されます。
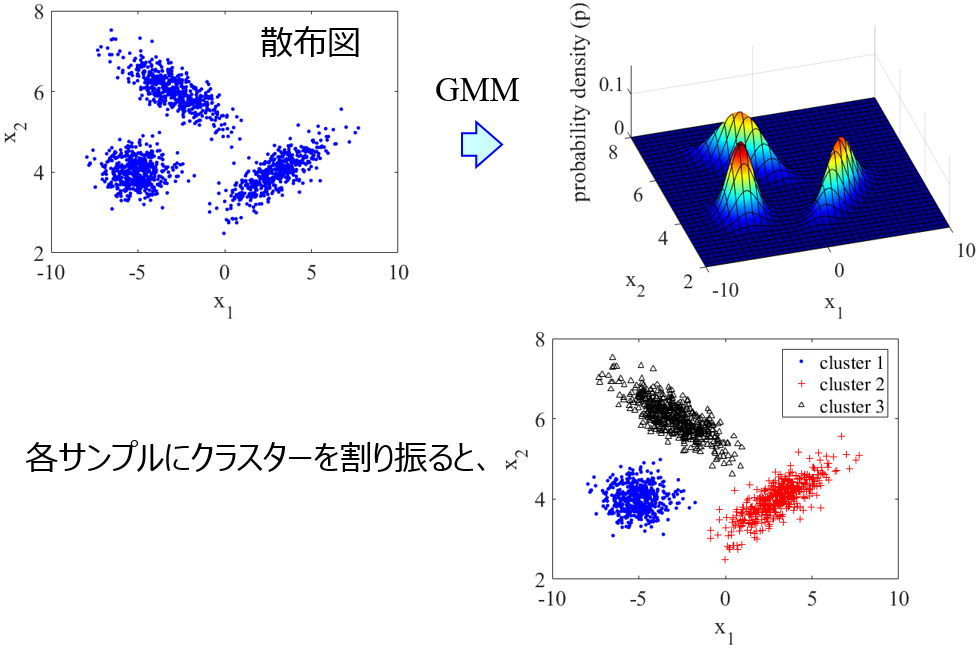
その後、クラスターごとに x とその時間遅れを同時に最適化します。これには Genetic Algorithm-based process Variable and Dynamics Selection (GAVDS) を用いました。
クラスターごとに、選択する領域の数も変えながら、x とその時間遅れを同時に最適化することで、複数セットの x とその時間遅れの組み合わせが得られます。
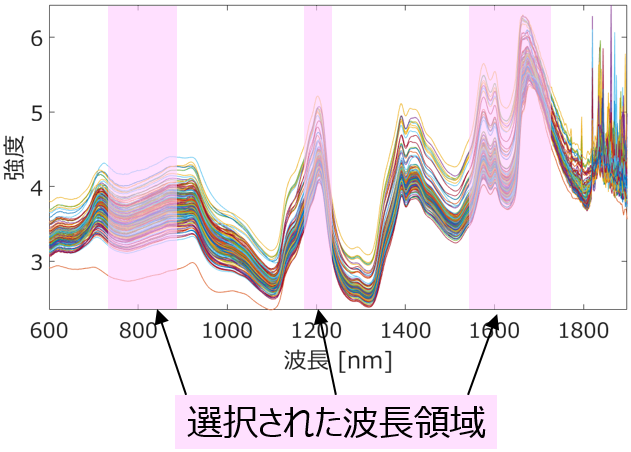
x とその時間遅れの組み合わせごとに、Locally Weighted Partial Least Squares (LWPLS) で適応型ソフトセンサーを構築・運用します。
y の予測をするときは、異なるプロセス状態において x やその時間遅れが最適化された、複数の LWPLS モデルが同時に予測しています。
たとえば 100 個の LWPLS モデルがあると、x (とその時間遅れ) の値を入力したときに、100 個の y の予測値が得られます。それらを、モデルごとの重みを考慮したアンサンブル学習により統合し、最終的な (一つの) y の予測値とします。具体的には、Midpoints between k-Nearest-Neighbor data points (MidKNN) で計算した RMSE の二乗の逆数に基づいて、予測するごとに重みを決定しています。
これにより、予測している時刻におけるプロセス状態が得意な LWPLS モデル (そのプロセス状態に特化した x やその時間遅れで構築された LWPLS モデル) の重みが大きくなるように、y を予測できます。
開発した適応型ソフトセンサーの名前は EGAVDS-LWPLS です。
EGAVDS-LWPLS を実際の二つのプラントのデータセットを用いて検証することで、従来の LWPLS モデルや、単純に GAVDS で x やその時間遅れを最適化したあとに構築された LWPLS モデルと比較して、予測精度が大幅に向上すること、そしてプロセス状態ごとに的確に y の値を予測できることを確認しました。
興味のある方は、ぜひ論文をご覧いただければと思います。どうぞよろしくお願いいたします。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。