回帰分析やクラス分類などの教師あり学習における各手法のハイパーパラメータ (PLS における成分数や SVR における C, ε など) と比べて、データの可視化やクラスタリングなどの教師なし学習における各手法のハイパーパラメータ (t-SNE の perplexity やクラスターの数など) を決めることは難しいです。これは、教師なし学習ではラベル付きデータがないため、何が最適か評価することが難しいことに由来します。ただ、ある程度妥当なやり方で教師なし学習の手法でもハイパーパラメータを決めることができた方がよいため、これまでデータの可視化手法については、ハイパーパラメータを自動的に決める方法を提案しました。
今回は、任意のクラスタリング手法におけるクラスター数を自動的に決める方法を考案しましたので、Python プログラムと一緒に紹介します。
もちろん、これまでにもクラスタリングにおいてクラスター数を決めるための方法はありました。ただ、使用できるクラスタリング手法が限られていたり、分布を仮定する必要があったり、指標はある一方で具体的な決め方が曖昧だったりしました。また、直感的にも理解できたり、納得感があったりする方法の方がよいと思い、今回は新たに考案しました。
クラスター数を決めるときの指標は、
自分 (サンプル) と距離の最も近い k 個のサンプルが、自分のクラスターと一致する割合
です。クラスター数を決めてクラスタリングした後に、サンプルごとに最も近い k 個のサンプルを集め、対象のサンプルのクラスターと k 個のサンプルのクラスターが一致するかを確認します。サンプル数が 100 で k = 3 のときは、100 × 3 = 300 個について、クラスターが一致するかを調べることになります。一致した数を 300 で割ったものが一致割合です。クラスター数を 1, 2, 3, … と大きくしながら、一致割合を求めていったときに、一致割合が 1 (100 %) となる最大のクラスター数を最適クラスター数とします。
=== 一致割合が 1 となる最大のクラスター数で選ぶ理由 ここから ===
本来は一つのクラスターであるべきサンプル郡が、二つのクラスターに分かれていると、あるサンプルと隣の (近い) サンプルが別のクラスターという状況になります。このときは、クラスターを細かく分けすぎといえます。この状況を判定できればよいと考え、自分のクラスターと、近くにあるサンプルのクラスターが一致割合を考えました。自分のクラスターと、近くにあるサンプルのクラスターが一致していれば、そのクラスターはよく固まっているといえます。ただ、それだけでは一つの大きなクラスターであればよいことになってしまいます。そもそもクラスタリングは、固まったサンプル群に分割することが目的であるため、よく固まっている中でも、クラスターが多いものを最適なクラスター数としました。
=== 一致割合が 1 となる最大のクラスター数で選ぶ理由 ここまで ===
今回のクラスター数を自動的に決める方法の Python コード (サンプルプログラム) は DCEKit にあり、demo_decide_number_of_clusters.py です。
こちらにあります→ https://github.com/hkaneko1985/dcekit
サンプルデータセットとしてあやめのデータを使用しています。クラスタリング手法は階層的クラスタリングのウォード法です (一例です)。また今回は、クラスタリングの結果を確認するために、t-SNE で可視化したあとの 2 次元平面上でクラスタリングを行っています。ただ、今回は結果を把握するために 2 次元平面上でクラスタリングしただけであり、本来は多次元空間 (元のデータセット) でクラスタリングすることが望ましいですので、ご注意ください。
t-SNE の perplexity を変えることで、二次元平面が変わります。そこで今回は、perplexity を変えたときの二次元平面ごとに、妥当なクラスター数を選べているか検証しました。なお、今回は一致割合でクラスター数を決められるかの検証を行うために、このようなことを実施しただけですので、実際の場合は、(t-SNE を実行する前の) オリジナルのデータセットで一致割合でクラスター数を決めたり、クラスタリングを行ったりしてください。
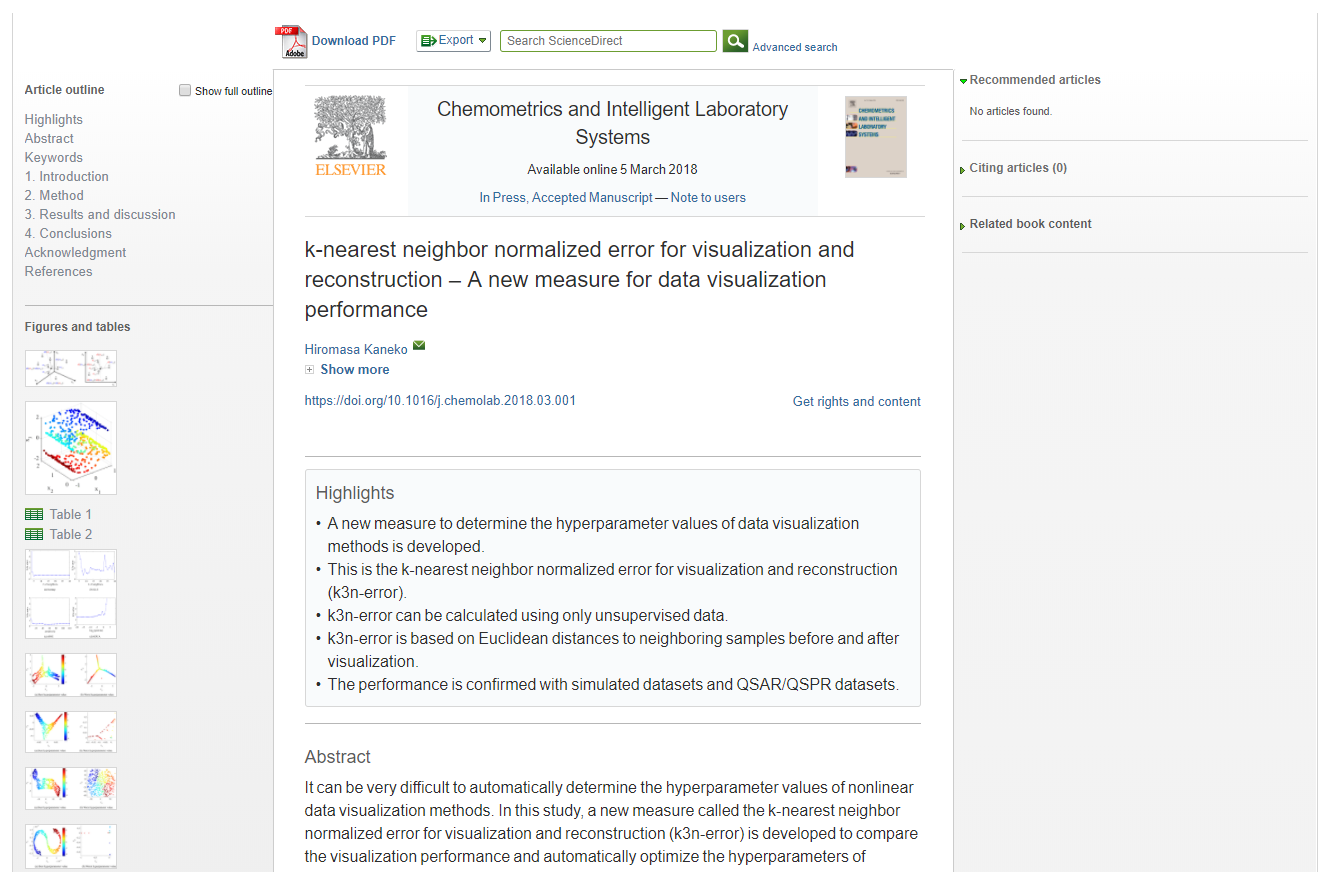
t-SNE の perplexity を 50 にすると以下のような二次元平面になりました。
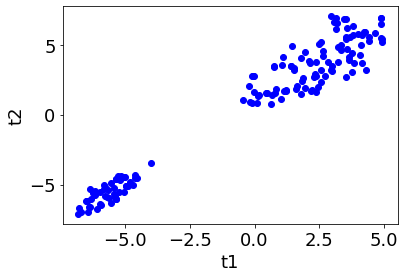
このとき、クラスターの数を 1, 2, …, 10 と増やしながら一致割合を計算すると、下のような図になります。なお今回は k = 3 としています。
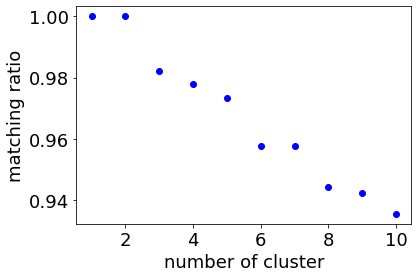
上図より、クラスター数が 2 を超えると一致割合が 1 ではなくなるため、最適クラスター数は 2 になります。このときのクラスタリングの結果が以下の通りであり、妥当な結果と考えられます。
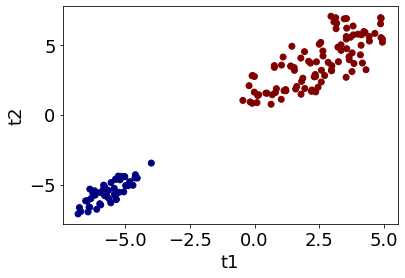
また perplexity が 5 のときは以下の結果になりました。
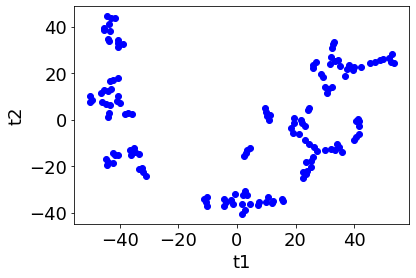
このとき、クラスターの数を 1, 2, …, 10 と増やしながら一致割合を計算すると、下のような図になります。
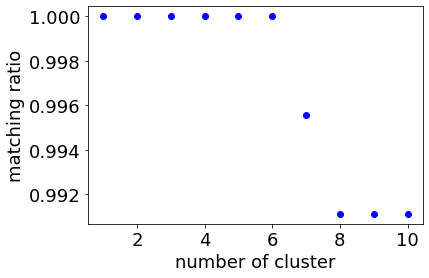
上図より、クラスター数が 6 を超えると一致割合が 1 ではなくなるため、最適クラスター数は 6 となります。このときのクラスタリングの結果が以下の通りであり、妥当な結果と考えられます。
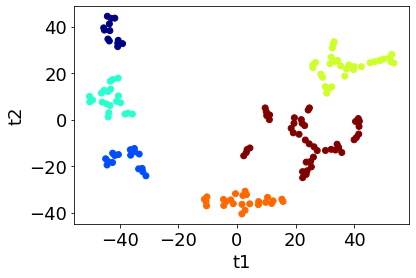
以上のように、一致割合によって最適クラスター数を決めることができます。
今回は階層的クラスタリングのウォード法を用いましたが、他にもいろいろなクラスタリング手法がありますので、各手法でクラスター数を決め、最も大きいクラスター数と手法の組み合わせを選ぶとよいかと思います。
何らかの方法でクラスター数を決めたい場合はぜひご活用いただけますと幸いです。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。

