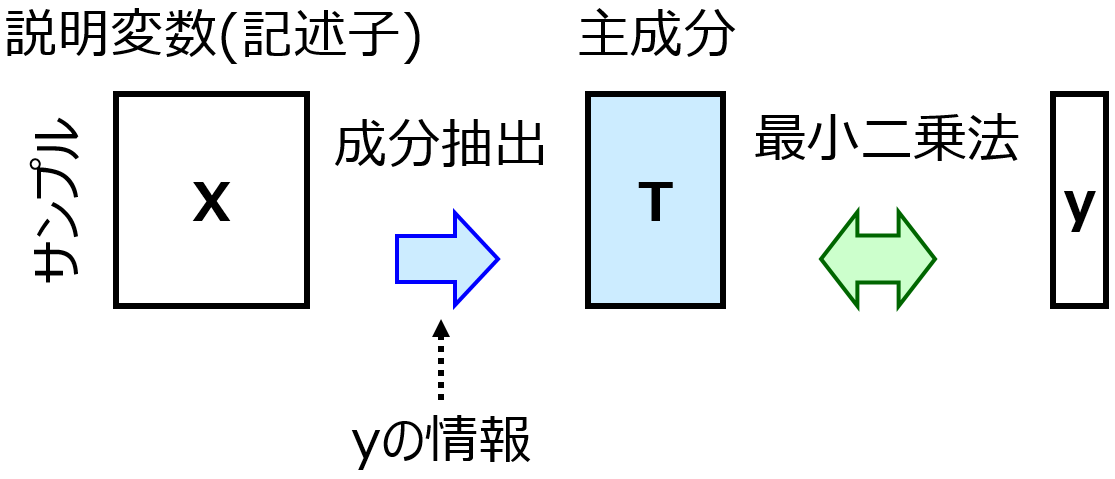
主成分分析(Principal Component Analysis, PCA)について、pdfとパワーポイントの資料を作成しました。データセットが与えられたときに、PCAで何ができるか、どのようにPCAを計算するかが説明されています。pdfもスライドも自由にご利用ください。

pdfファイルはこちらから、パワーポイント(pptx)ファイルはこちらからダウンロードできます。

興味のある方はぜひ参考にしていただき、どこかで使いたい方は遠慮なくご利用ください。

PCAの概要

• 見える化 (可視化) する手法
• 多変量 (多次元) のデータセットを低次元化する方法
• データセットのもつ情報量をなるべく失わないように元の次元から より低い次元でデータセットを表現
• “より低い次元” を２次元にすれば可視化を達成
• 軸を回転 (＋反転) させる

スライドのタイトル

• 主成分分析 (PCA) とは？
• PCAの図解
• PCAで できること
• データセットの表し方
• PCAの前に
• 2変数のときのPCA (3変数以上への拡張も簡単)
• 主成分とローディング
• 行列で表すと・・・
• 第１主成分を考える
• ローディングの規格化条件
• 主成分の分散を最大化
• Sを最大化するローディングを求める
• Lagrangeの未定乗数法
• Gを偏微分して 0
• 行列で表す
• 固有値問題へ
• 寄与率
• 累積寄与率
• 逆写像
• 逆写像のしかた

参考資料

• 宮下芳勝・佐々木慎一，コンピュータ・ケミストリー シリーズ３ ケモメトリックス－化学パターン認識と多変量解析－，共立出版 (1995)
• S. Wold, Principal component analysis. Chemometrics and Intelligent Laboratory Systems, 2, 37−52, 1987.

PCAのPythonのプログラムは、こちらの課題4,5,6をご参照ください。

以上です。

質問・コメントがありましたら、twitter・facebook・メールなどを通して教えていただけるとうれしいです。