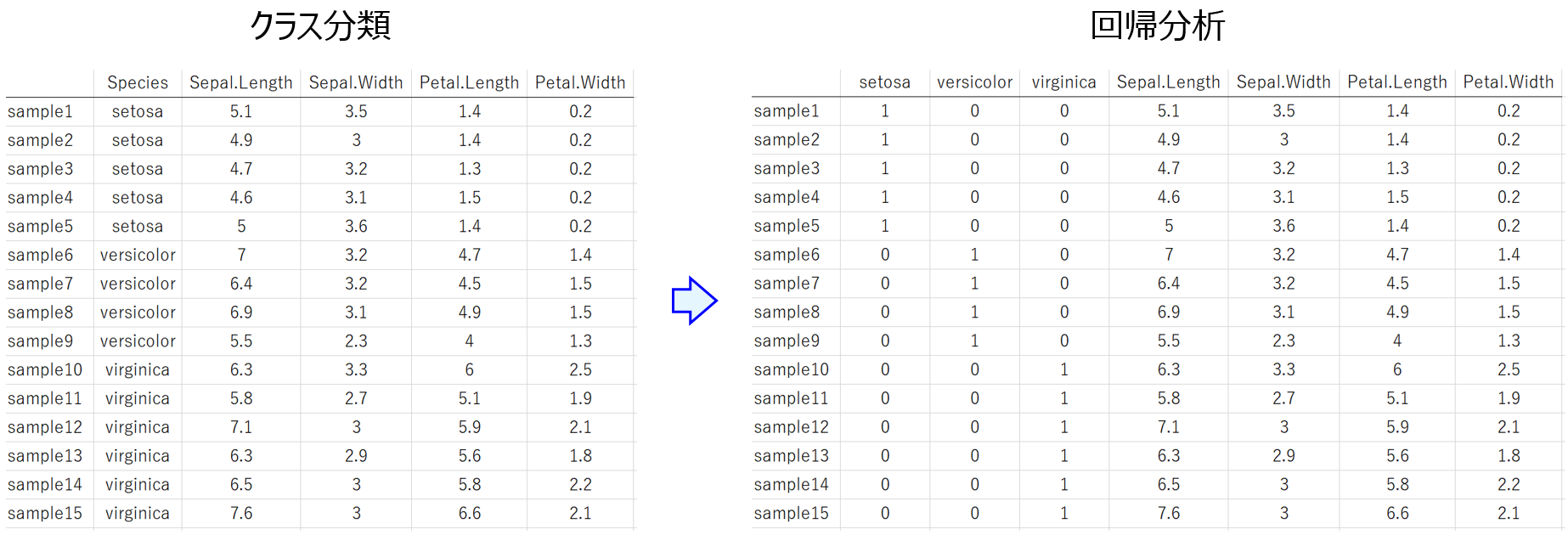
いろいろなところで、ディープラーニング (deep learning) とか深層学習とかディープニューラルネットワークとかを耳にすると思います。実際にニューラルネットワークのモデルを構築したことがある人もいるかもしれません。ディープラーニングは隠れ層の層の数を多くしたニューラルネットワークを学習することであり、基本的には以下の逆誤差伝播法で学習できます。
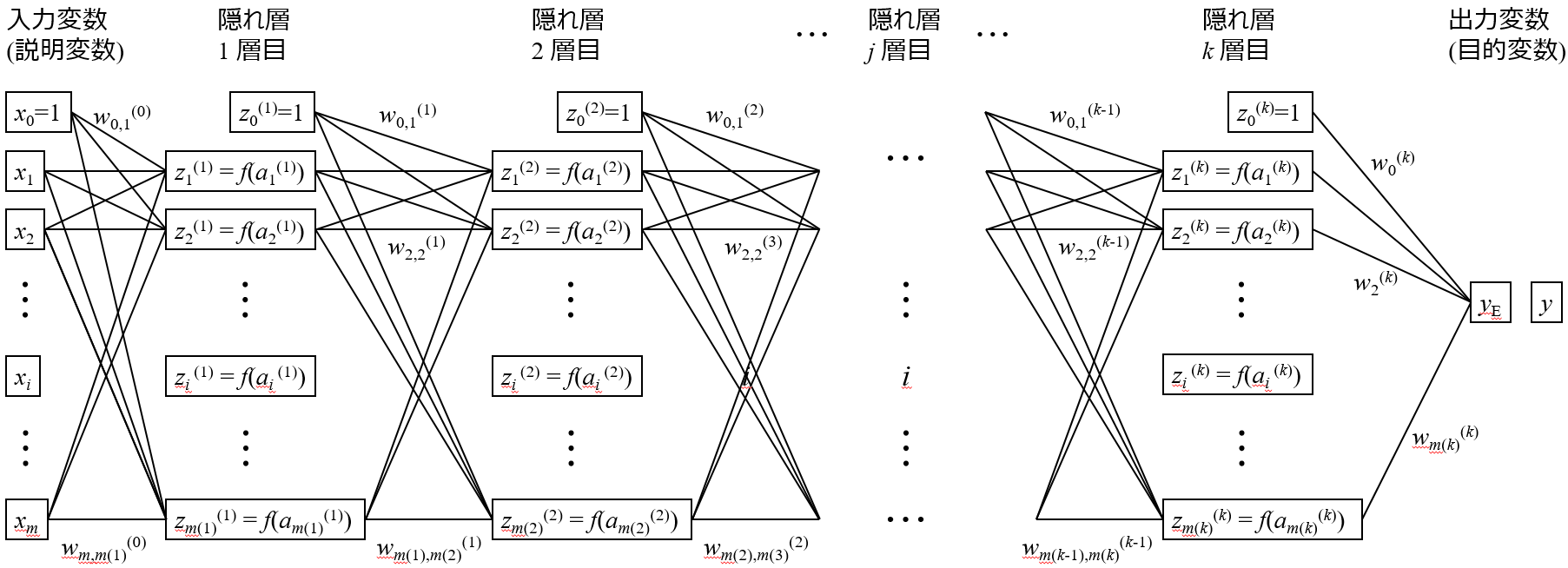
逆誤差伝播法の原型は、David E. Rumelhart たちによって、1986年に発表されました。
それから、ディープニューラルネットワークである隠れ層を多層にしたニューラルネットワークをはじめとする、いろいろなニューラルネットワークが出てきて、「ニューラルネットワークは素晴らしい精度だ!」 と、論文発表も盛んになります。
しかし、ニューラルネットワークにはいくつか問題がありました。最も大きな問題の一つが、過学習 (オーバーフィッティング) です。単純なネットワークで、隠れ層が1層のときを考えてみましょう。仮に、入力変数 (説明変数) の数を 100、隠れ層のニューロンの数を 50、出力変数 (目的変数) の数を 1 としましょう。このとき、最適化する重みの数は、(100+1) × 50 + (50+1) × 1 = 5101 です。つまり、隠れ層が1層の、お世辞にも “ディープ” ニューラルネットワークとはいえないシンプルなニューラルネットワークでさえ、5000以上の自由度をもつ非常に複雑な非線形モデルになるのです。この非線形モデルの5000以上のパラメータを学習 (フィッティング) することになりますが、たかだか 1000 程度のサンプル数では、いかようにもフィッティングできてしまい、トレーニングデータの誤差を 0 にできてしまうわけです。完全にオーバーフィッティングです。隠れ層の層の数を増やすと、指数関数的に重み (フィッティングするパラメータ) の数が増え、もう目も当てられません。
たしかにニューラルネットワークを使えば誤差の小さいとても精度の高いモデルができるよね、でもモデルに新しいデータを入力して推定させたときに、全然当たらないよね。
というわけです。
もちろん、パラメータの数が増えると、それだけニューラルネットワークの学習にかかる計算コストも大きくなります。モデルを構築するのに時間がかかってしまうわけです。このように、ニューラルネットワークは自由度の高い非常に強力な手法ですが、その強力さゆえ、扱いにくいモデルだったのです。
そこで、オーバーフィッティングを防ぐ手法が流行りだします。モデルの複雑度にあえて罰則をつけて自由度を抑える正則化を盛り込んだサポートベクターマシン (Support Vector Machine, SVM)・サポートベクター回帰 (Support Vector Regression, SVR) などや、モデルをたくさん作って (それらはオーバーフィットしていても) それらを総合的に用いて推定値のばらつきを抑えるランダムフォレスト (Random Forest, RF) などのアンサンブル学習です。
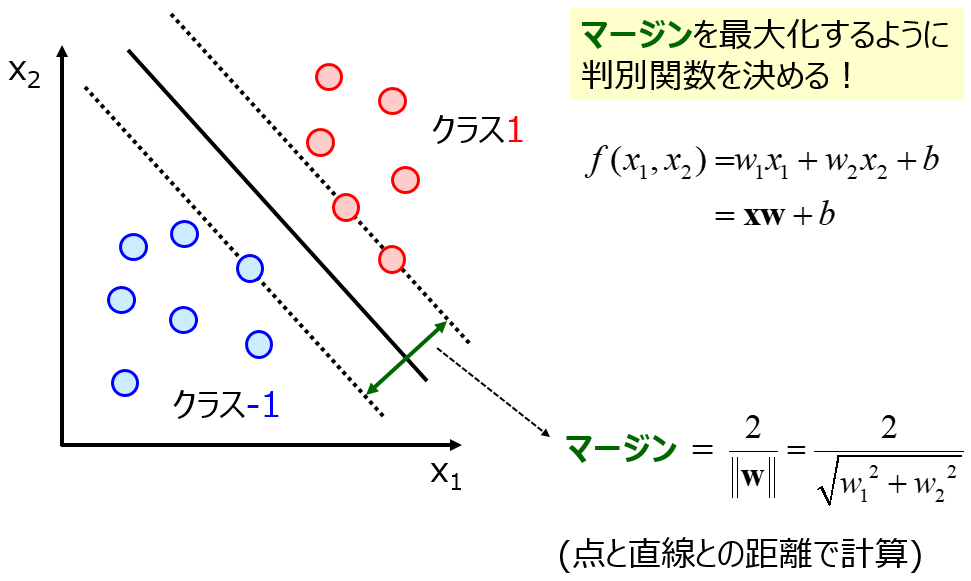

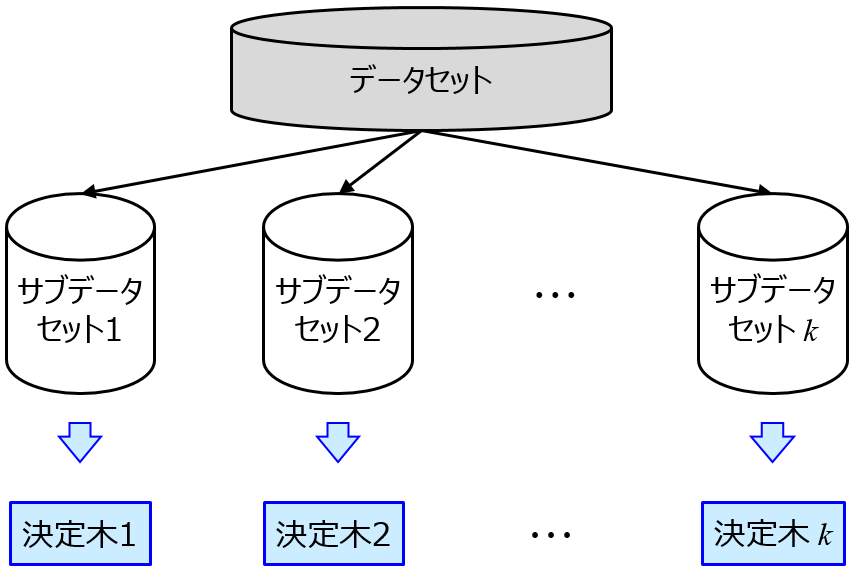
これらは今でもよく用いられる手法ですね。サンプルが多くない場合でも、オーバーフィッティングをうまく回避してモデルを構築できます。
そうこうしているうちに、時代がニューラルネットワークに追いついてきました。つまり、ビッグデータ時代の到来です。サンプル数が非常に大きくなり、”ディープ” ニューラルネットワークでもオーバーフィットしにくくなりました。さらにいうと、多様性の高い、膨大な数のサンプルがある中でモデル構築するとき、自由度の非常に高いディープニューラルネットワークのほうが、適切にモデリングできるのです。もちろん、ディープラーニングの流行には教師なしデータを使った事前学習やReLU (Rectified Linear Unit) の開発の貢献も大きいと思いますが、やはりディープラーニングにより適切にモデル構築するためにはサンプルの多様性とサンプル数が不可欠です。また、計算機の性能も高くなり、膨大な数のパラメータを現実的な時間にフィッティングできるようになったのも大きいです。
このように、ビッグデータを背景にしてディープラーニングが流行りだしたわけです。大切なことは、適切にディープラーニングして、ディープニューラルネットワークを構築するためには、多様性の高い、膨大な数のサンプルが必要ということです。そうでないとき、サンプルの多様性もサンプル数もほどほどのときは、
- サポートベクターマシン (Support Vector Machine, SVM)
- サポートベクター回帰 (Support Vector Regression, SVR)
- ランダムフォレスト (Random Forest, RF)
などが優れていることが多いです。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。