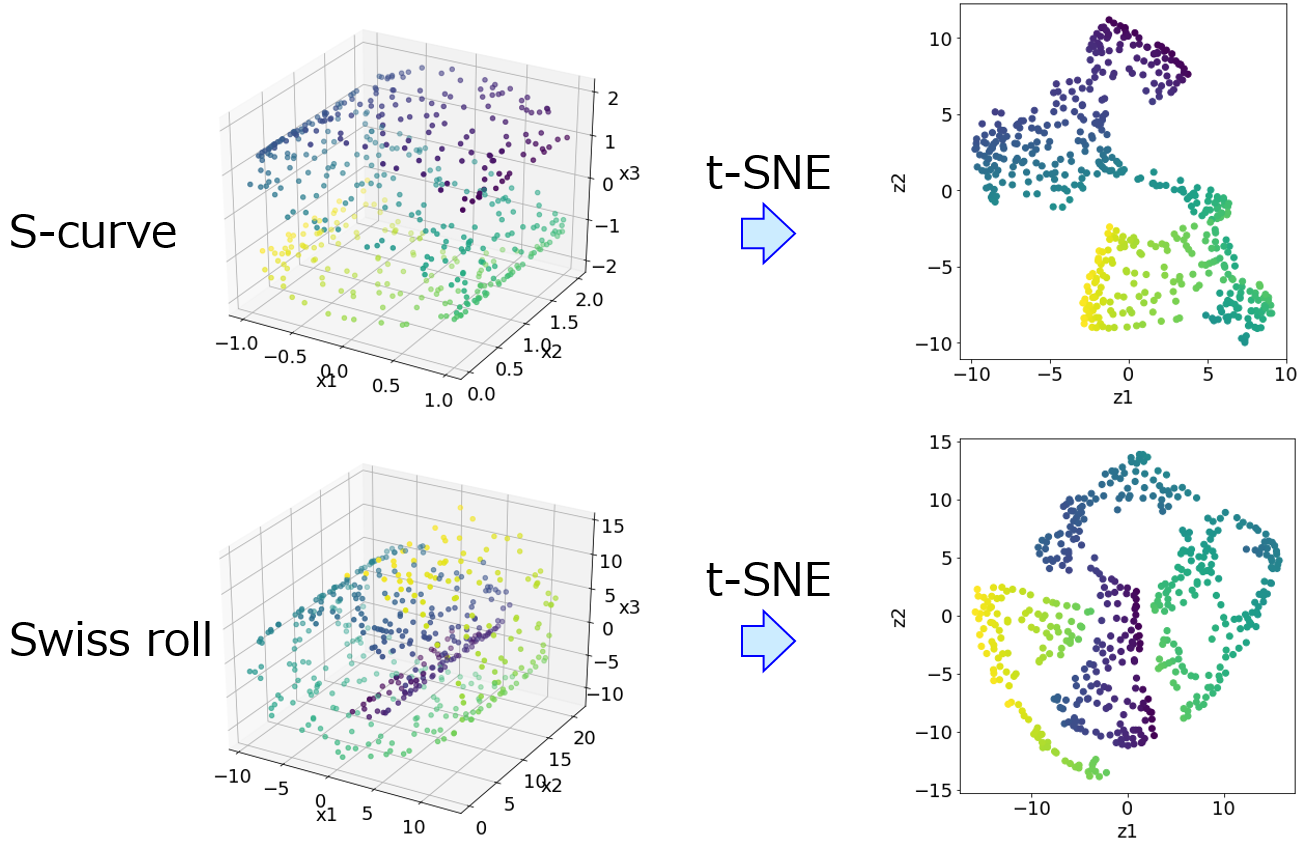
今回は、t-distributed Stochastic Neighbor Embedding (t-SNE)についてです。変数 (特徴量・記述子など) がたくさんある (多変量・多次元の) データセットが与えられたときに、適切に２次元平面にデータの可視化をする手法です。

そんなt-SNEについて、pdfとパワーポイントの資料を作成しました。t-SNEの具体例や計算方法について説明されています。pdfもスライドも自由にご利用ください。

pdfファイルはこちらから、パワーポイント(pptx)ファイルはこちらからダウンロードできます。

興味のある方はぜひ参考にしていただき、どこかで使いたい方は遠慮なくご利用ください。

また、こちらのGitHubに、t-SNE をプログラムで実行する解析例 (デモ) や、t-SNE における perplexity を最適化するデモを用意しました。ぜひご活用ください。

t-SNE の概要

• 非線形の可視化手法の一つ
• PCA や GTM のように、元の空間から低次元空間 (基本的には二次元平面) に写像させる関数が得られるわけではないので注意
• 写像というよりは、サンプル全体が見やすいように二次元平面に配置するイメージ
• 可視化に特化した手法
• 元の空間におけるサンプル間の距離関係が二次元平面におけるサンプル間の距離関係として保持されるほど値が小さくなる目的関数を準備して、それが小さくなるように二次元平面にサンプルを配置させる

スライドのタイトル

• t-SNE とは？
• t-SNE のイメージ
• 文字の定義
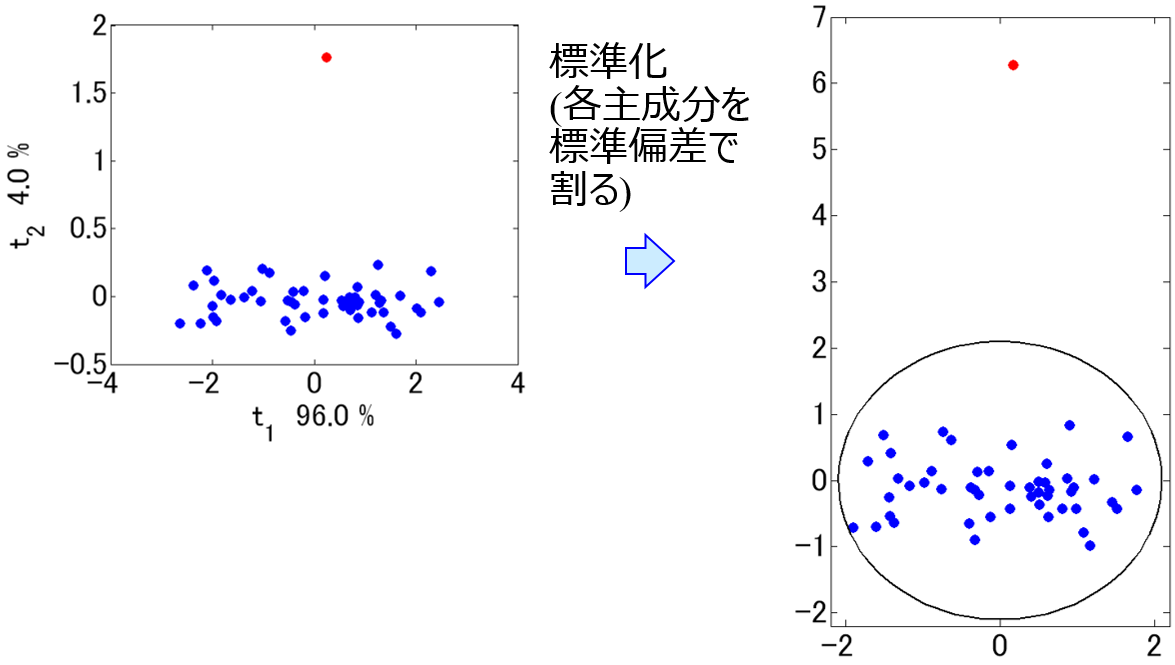
• 前処理
• t-SNEでは何をしているか？
• p(x⁽ⁱ⁾, x^(j)) って何？
• p(x^(j) | x⁽ⁱ⁾) って何？
• x⁽ⁱ⁾ と x^(j) の距離と p(x⁽ⁱ⁾, x^(j)) の関係
• p(x⁽ⁱ⁾ | x^(j)) の σ_i はどうする？
• p(z⁽ⁱ⁾, z^(j)) って何？
• p(z⁽ⁱ⁾, z^(j)) の式
• 目的関数 C の最小化
• z⁽ⁱ⁾ の初期値
• t-SNE をやってみる
• perplexity をどう決めるか？
• 参考文献

以上です。

質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。