統計だったり機械学習だったりニューラルネットワークだったり、データを使ったモデルの開発をしていますと、

いくつサンプルがあったらモデルはできますか？

ってよく聞かれます。今回はこの質問に答えながら、モデルの適用範囲・モデルの適用領域について説明します。

まずいきなりですが、質問の答えは

サンプル数はいくつでも、モデルは作れる

です。ただし補足があります。それは

サンプル数やその内容によって、モデルを適用できるデータ範囲・データ領域が異なる

ということです。

例をつかって説明します。説明変数(記述子・入力変数) x が１変数、目的変数(出力変数) y が１変数とします。

下の図のように３つのサンプルがあるときを考えます。

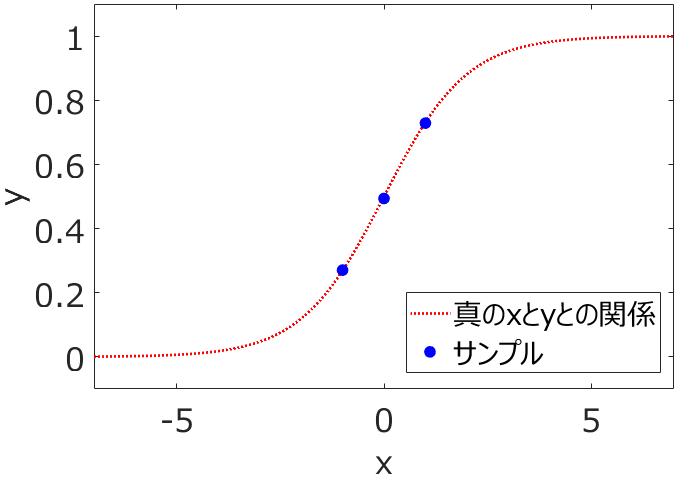
赤い点線が真のxとyとの関係であり、その関係にしたがうように今回は３サンプルが生成されています。

この３サンプルを使って、xとyとの関係について直線で回帰モデルを作ると

y = 0.23 x + 0.5

となります。

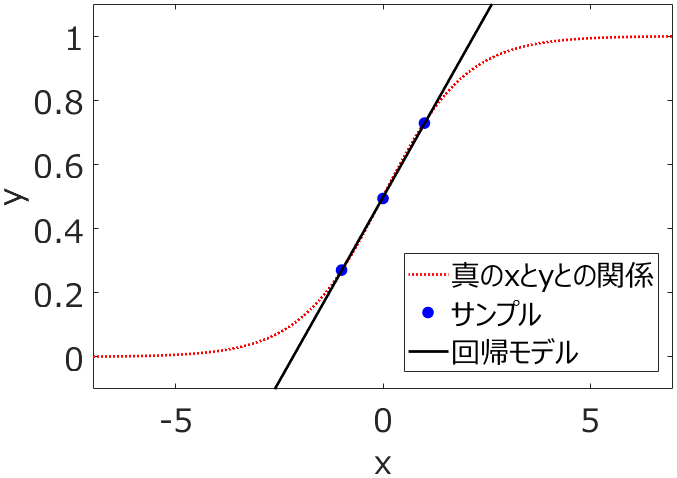
最小二乗法で実際に計算した結果です。このように、たった３サンプルでもモデルは作れます。

ただ、上の図を見るとわかるように、xの値が大きくなったり、逆に小さくなったりすると、真のxとyとの関係と、回帰モデルとのズレが大きいことがわかります。ズレが大きいということは、回帰モデルによって推定されたyの値と、実際のyの値との誤差が大きい、ということです。このようなxの範囲では、回帰モデルを使っても意味がありません。

つまり、３サンプルでもモデルは作れますが、そのモデルを適用できるxのデータ範囲は、-1から1くらいまでですよ、ということです。この ”xのデータ範囲” のことを、モデルの適用範囲といったりモデルの適用領域といったりします。英語だとApplicability Domain (AD) です。

次に、３サンプルよりたくさんのサンプルが得られたとしましょう。

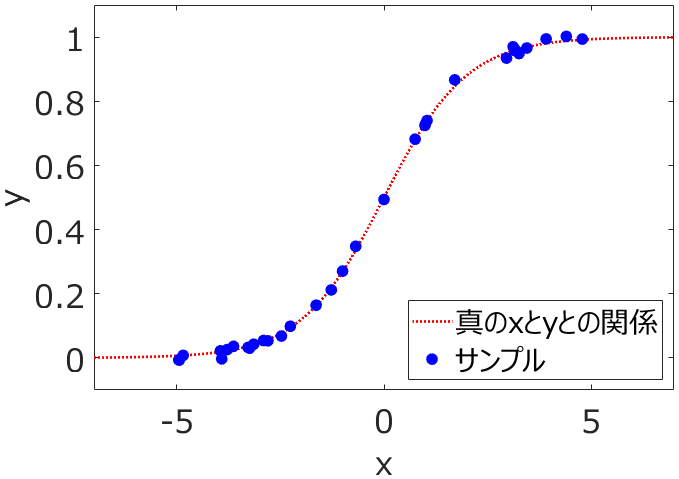
これらのサンプルを使って、非線形の回帰モデルを作ると

y = 0.2 x + -0.0007 x² -0.004 x³ + 0.5

となりました。

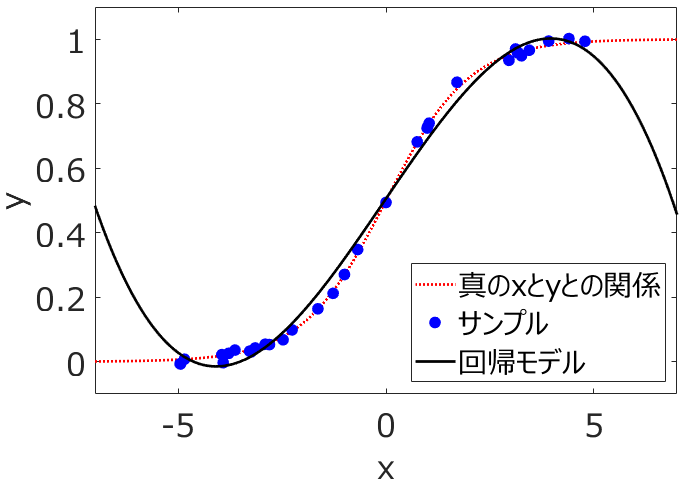
これも実際に最小二乗法で計算した結果です。３サンプルのときと比べると、xの広い範囲で赤線の真のxとyとの関係と黒線の回帰モデルとのズレが小さいです。つまり、

サンプル数を増やすことでモデルの適用範囲・モデルの適用領域が広がった

というわけです。ただ、上図を見ても分かるように、モデルの適用できるデータ範囲は、-5から5くらいまでであり、それをこえてしまうと回帰モデルによるyの推定値と実際のyの値との誤差が大きくなってしまいます。モデルの適用範囲・領域は -5から5くらいまで、ということです。

さらに、今回は-5から5くらいまでのサンプルがまんべんなくあったため、モデルの適用範囲・領域を-5から5くらいまでに設定できましたが、たとえば-1から1くらいの間に固まってサンプルが得られたら、モデルの適用範囲・適用領域を-1から1くらいまで、になってしまいます。サンプルの数だけでなく、サンプルの内容も重要ということです。

モデルの適用範囲・モデルの適用範囲の決め方

では、実際はどのようにモデルの適用範囲・領域を決めるのでしょうか？もちろん、上の例のようにxの値の範囲で決めることもできます、ただ実際はxの変数の数はたくさんあることが多いため、それらの複数の変数をいっしょに考えて決めたほうが効率的です。

一番単純なモデルの適用範囲・適用領域の決め方は、中心からの距離をつかう方法でしょう。中心、つまり平均、からの距離がいくつまでがモデルの適用範囲・領域である、のように設定します。これなら、xのすべての変数を同時に考慮してモデルの適用範囲・領域を決められます。

ただ、中心からの距離は、サンプルが中心から同心円状にちゃんと分布しているときにしか、うまくいきません。

そこでわたしは、データ密度を使う方法をオススメしています。あるサンプルがモデルの適用範囲・領域かどうかを考えるときに、そのサンプルの周りにどれくらいモデルを構築したサンプルがあるか、を考えるわけです。近くにたくさんサンプルがあれば、データ密度は高くなり、モデルの適用範囲・領域の中、といえます。

データ密度の指標として、簡単なのは最も距離の近いk個のサンプルとの距離の平均でしょう。あるサンプルについて、モデルを構築したすべてのサンプルとの距離を計算し、それを小さい順にk個取り出し、その平均値を計算するわけです。その平均値が小さいほど、データ密度は高い、ということになります。kは5とか10とか使う人が多いと思います。

ちなみに、データ密度の指標として少し複雑なものに、one-class support vector machineを使ったものもあります。

以上です。

質問・コメントがありましたら、twitter・facebook・メールなどを通して教えていただけるとうれしいです。