リッジ回帰(Ridge Regression, RR), Least Absolute Shrinkage and Selection Operator (LASSO), Elastic Net (EN) について、pdfとパワーポイントの資料を作成しました。データセットが与えられたときに、RR, LASSO, ENで何ができるか、それぞれの特徴、どのように計算するかが説明されています。pdfもスライドも自由にご利用ください。
pdfファイルはこちらから、パワーポイント(pptx)ファイルはこちらからダウンロードできます。
興味のある方はぜひ参考にしていただき、どこかで使いたい方は遠慮なくご利用ください。
RR, LASSO, ENの概要
- 線形の回帰分析手法
- 目的変数の誤差の二乗和に加えて、それぞれ以下の項を最小化することで、過学習を防ぐ
- RR: 回帰係数の二乗和
- LASSO: 回帰係数の絶対値の和
- EN: 回帰係数の二乗和と絶対値の和 (RRとLASSOとの中間)
- LASSOとENは回帰係数の値が0になりやすく、変数選択としても利用できる
スライドのタイトル
- RR・LASSO・EN とは?
- OLS・RR・LASSO・EN・SVR
- OLS・RR・LASSO・EN・SVRの共通点
- OLS・RR・LASSO・EN・SVRの違い 1/2
- OLS・RR・LASSO・EN・SVRの違い 2/2
- 回帰係数の求め方
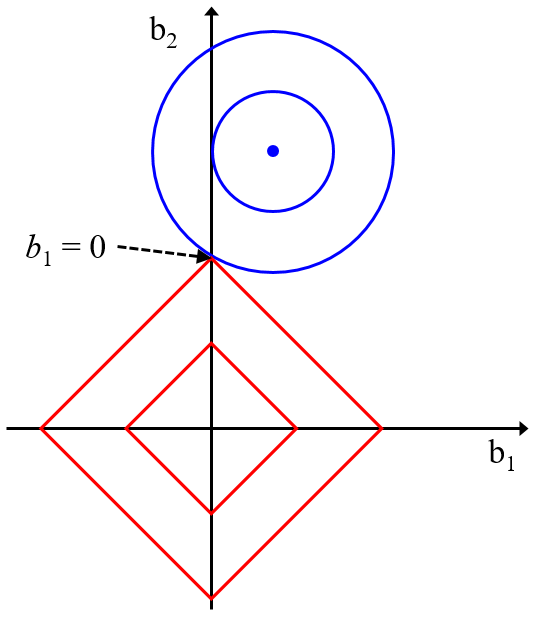
- どうしてLASSOは回帰係数が0になりやすいの?
- 重み λ, α の決め方
参考資料
- Jared P. Lander, みんなのR -データ分析と統計解析の新しい教科書-, マイナビ (2015)
- C.M. ビショップ,パターン認識と機械学習 上, 丸善出版 (2012)
RR, LASSO, ENのPythonのプログラムは、こちらの課題16をご参照ください。
以上です。
質問・コメントがありましたら、twitter・facebook・メールなどを通して教えていただけるとうれしいです。