応化先生と生田さんが過学習 (オーバーフィッティング) について話しています。
応化:今日は過学習についてです。
生田:過学習?学習し過ぎるってこと?
応化:その通りです。
生田:だったら悪いことじゃなさそうに聞こえるけど・・・。学習をたくさんするんだからいいことじゃない?
応化:じつは違うんです。たとえば、高校の数学で微分の勉強をするとき、例題を解きますよね。
生田:はい。
応化:普通は、例題で解き方を学ぶと思います。ただ、過学習のイメージは、例題と答えの一言一句を覚えるくらいやってしまう感じです。
生田:ものすごいですね。
応化:一言一句覚えたからと言って、別の問題が出てきたときに解けるわけではないですよね。
生田:確かに、解き方を学んだほうがいろいろな問題に応用できそうですね。
応化:そういうことなんです。人工知能を作成したり、機械学習を行ったりするときにも、過学習が起こってしまうんです。
生田:人工知能や機械学習での過学習ってどういう現象ですか?
応化:お答えしますね。例を示しながら説明したほうがわかりやすいので、下の図のようなデータがあるときを考えましょう。
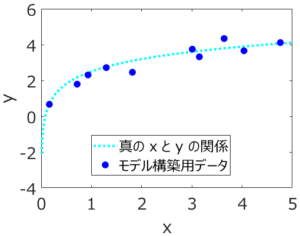
生田:x と y の散布図ですね。10点のサンプルがあります。
応化:はい、ちなみに水色の点線は、真の x と y との関係です。本来は水色の点線上にサンプルが来るはずですが、y には測定誤差のあるため、少しズレた形で、x と y が10点測定された、という状況を仮定しています。
生田:なるほど。
応化:x から y を推定する回帰モデル (人工知能, y = f(x) ) を機械学習で求めることを考えます。
生田:どうやって求めるのですか?
応化:今回は、以下の2つのモデルを仮定しましょう。
モデルA・・・ y = a0 + a1x + a2x2 + a3x3
モデルB・・・ y = b0 + b1x + b2x2 + b3x3 + b4x4 + b5x5 + b6x6 + b7x7 + b8x8 + b9x9
生田:モデルAが x の 3 次式、モデルBが x の 9 次式ですね。a0, a1, a2, a3 とか、b0, b1, b2 などはどうやって求めるんですか?
応化:今回は最小二乗法による線形重回帰分析で求めましょう。
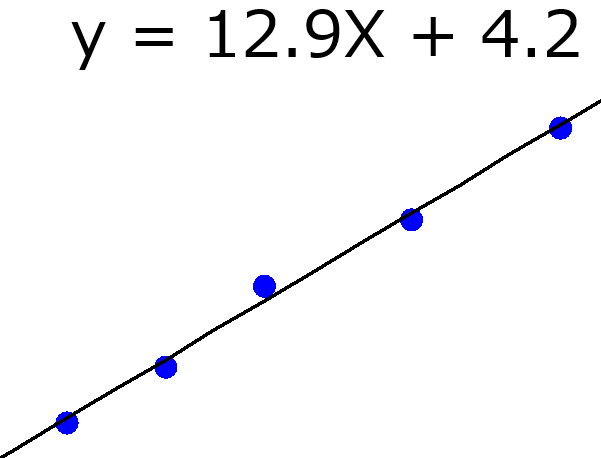
生田:了解です。yの誤差の二乗和が小さくなるように求めるんですね。
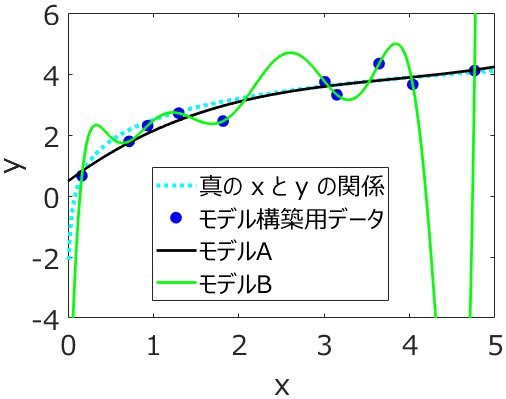
応化:その通りです。求めた後に、モデルAとモデルBを図示した結果が下にあります。
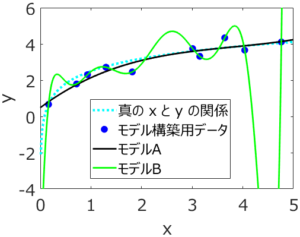
生田:モデルBの線はクネクネしてますね。
応化:はい、すべてのモデル構築用データを正確に通っていることが分かります。モデル構築用における y の実際の値と、モデルBによって計算された値の誤差がほとんど 0 ってことです。
生田:誤差 0 ってことはいいことですよね。
応化:本当にそうでしょうか。確かに、最小二乗法では、そのようになるように計算を行い モデルBの係数を求めています。ただ、yには測定誤差もありますので、誤差が 0 になるのは不自然です。しかも、モデルBの型 (y = b0 + b1x + b2x2 + b3x3 + b4x4 + b5x5 + b6x6 + b7x7 + b8x8 + b9x9) が真の x と y の関係の形とも限りません。
生田:確かに。
応化:そして、図をよく見ると水色の点線である真の x と y との関係からは大きく離れています。
生田:特に x が 4 から 5 の間では、図の外にふり切れちゃってますね。
応化:はい、x = 4.5 のときの y の値をモデルBで計算すると -10.7 になりますが、実際は 4.0 です。
生田:全然違う!モデルBは新しいサンプルを推定しようとすると、誤差が大きくなっちゃうのか。
応化:その通りです。このように、モデル構築用データに対して過度に学習することで、モデル構築用データの誤差は小さくなりますが、新しいデータにおける誤差が大きくなってしまうことを、過学習といいます。英語で言うと overfitting (オーバーフィッティング) です。
生田:モデルBは過学習がおきていたのか。過学習がおきるとモデルは使いものにならないですね。その点、モデルAはいい感じですね。真の x と y との関係とも近いです。
応化:そうですね。モデルAの黒い線とモデル構築用データとは多少離れていて、yの値に誤差はありますが、真の x と y との関係をうまく表現していますね。このようなときは、新しいサンプルの y の値を推定しても、モデル構築用データにおける誤差と同じような誤差で推定できます。
生田:y には測定誤差もあるので、多少誤差が生じるのは仕方ないですよね。
応化:はい。
生田:過学習が問題なことがわかりました。どのように過学習を防げばいいのでしょうか?
応化:過学習を防ぐ方法は、大きく分けて3つあります。一つの方法は、説明変数 (入力変数・記述子・特徴量) の数を減らしたり、データ量を圧縮したりすることです。
生田:数を減らす?データ量を圧縮?どういうことですか?
応化:数を減らすことについて、モデルAとモデルBを見てみましょう。モデルAは3次式で説明変数は3つですが、モデルBは9次式で説明変数は9つです。モデルBのように説明変数の数が多いと過学習しやすいので、減らすわけです。
生田:なるほど、変数選択ですね。
応化:はい。あとデータ量の圧縮は、主成分分析(Principal Component Analysis, PCA) とか 部分的最小二乗回帰(Partial Least Squares Regression, PLS) とかです。データを低次元化してから回帰分析します。

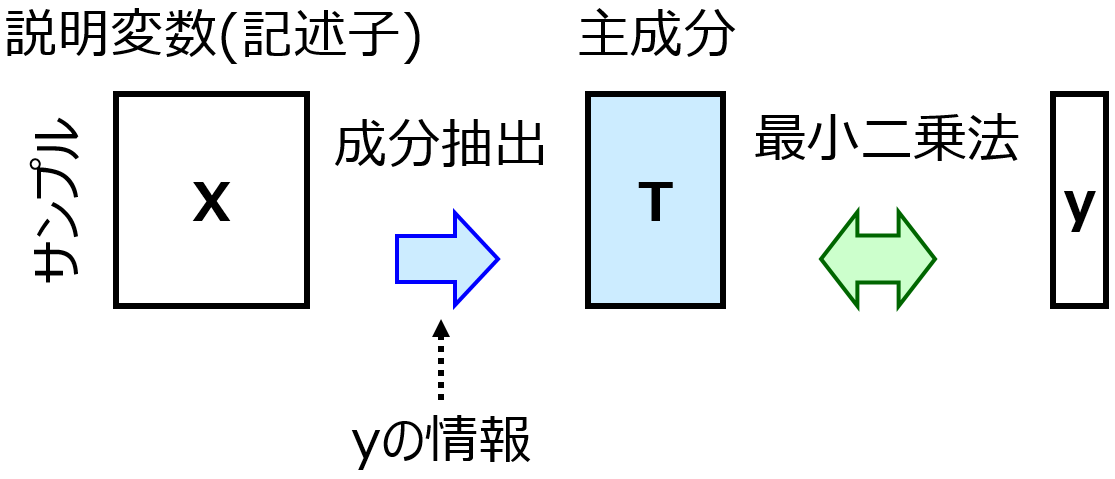
生田:勉強しておきます。
応化:特にPCAとPLSはデータ解析の最初に行う基本的な手法ですが、とても強力な手法ですので、しっかり理解しましょう。
生田:はい!
応化:過学習を防ぐ2つ目の方法を説明するために、モデルAとモデルBの係数を見てみましょう。
| a0 | 0.483 |
| a1 | 2.87 |
| a2 | -3.25 |
| a3 | 1.31 |
| b0 | -9.09 |
| b1 | 107 |
| b2 | -383 |
| b3 | 684 |
| b4 | -686 |
| b5 | 410 |
| b6 | -148 |
| b7 | 31.8 |
| b8 | -3.72 |
| b9 | 0.182 |
生田:モデルBの係数は、絶対値がとても大きいですね!
応化:いいところに気づきましたね。過学習するときには、係数の値が大きくなりがちなのです。なので、係数の値が大きくならないように、回帰分析を行うことで、過学習を防ごうとします。
生田:どんな方法がありますか?
応化:たとえば、リッジ回帰(Ridge Regression, RR), Least Absolute Shrinkage and Selection Operator (LASSO), Elastic Net (EN) などです。サポートベクター回帰(Support Vector Regression, SVR) もその仲間です。
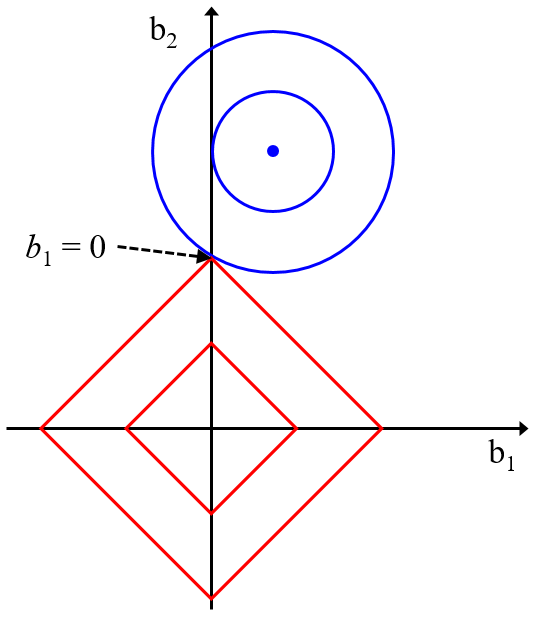

生田:たくさんありますね・・・。
応化:どれも原理は同じなので、一つ理解すると、他も理解しやすいですよ。
生田:わかりました!
応化:過学習を防ぐ3つ目の方法は、学習を途中でストップすることです。
生田:勉強をやめちゃう感じ?
応化:そうですね。たとえば、ニューラルネットワークを学習させるときに使われる誤差逆伝播法 (バックプロパゲーション, Backpropagation) において、学習すればするほど誤差は小さくなるのですが、途中でやめてしまうんです。
生田:どうやってやめるタイミングを決めるんですか?
応化:モデル構築用データとは別のデータセットを準備しておいて、そのデータセットの誤差が十分に小さくなったときとか、クロスバリデーションとかです。誤差逆伝播法は、深層学習 (ディープラーニング, deep learning)、ディープニューラルネットワーク (deep neural network) でも使われるので、理解しておきましょう。
生田:はい!
応化:以上が過学習とその対処法です。モデルを構築するときには、モデル構築用データにおける誤差だけでなく、新しいサンプルの誤差や、クロスバリデーションのときの誤差もしっかり確認して、過学習が起きているかどうかチェックしましょうね。

生田:わかりました!
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。