応化先生と生田さんがアンサンブル学習 (ensemble learning) について話しています。
応化:今日はアンサンブル学習 (ensemble learning) についてです。
生田:アンサンブル?音楽関係ですか?
応化:いえ、合奏とか合唱とかのアンサンブルではありません。ハーモニーという意味では同じかもしれませんが、今回は統計関係のアンサンブル学習です。
生田:お願いします!
応化:アンサンブル学習は、クラス分類モデルや回帰分析モデルの推定性能を上げるための方法の一つです。まずは簡単な例を見てみましょう。下の図をご覧ください。

生田:「+」と「-」をクラス分類するモデルが3つ、あと多数決ですか?
応化:そうですね。一番左が、正解のクラスです。+ と - とを分類する問題ですが、見やすいように3つのサンプルとも正解を + としています。3つのモデルの推定結果がその左です。それぞれ、一つだけ - と判定してしまい、正解率は 67% ですね。ただ、一番左の、3つのモデルの多数決をとった結果を見てみましょう。
生田:それぞれのサンプルで、- と判定しているモデルが1つありますが、残りの2つのモデルは + と判定しています。なので、多数決すると + になります。正解率 100% !
応化:その通りです。このように、複数の異なるモデルを構築して、推定するときはそれらのモデルの推定結果を統合するのがアンサンブル学習です。
生田:上の例では実際に正解率が上がっていますし、アンサンブル学習いい感じですね。
応化:もちろん、上は理想的な例ですので、いつもあんなに正解率が上がるわけではありません。ただ、基本的な理論は上の図の通りです。
生田:まさに、三人寄れば文殊の知恵、ですね。
応化:そうですね。わかりやすい例として、決定木 (Decision Tree, DT) をアンサンブル学習すると、ランダムフォレスト (Random Forests, RF) になります。
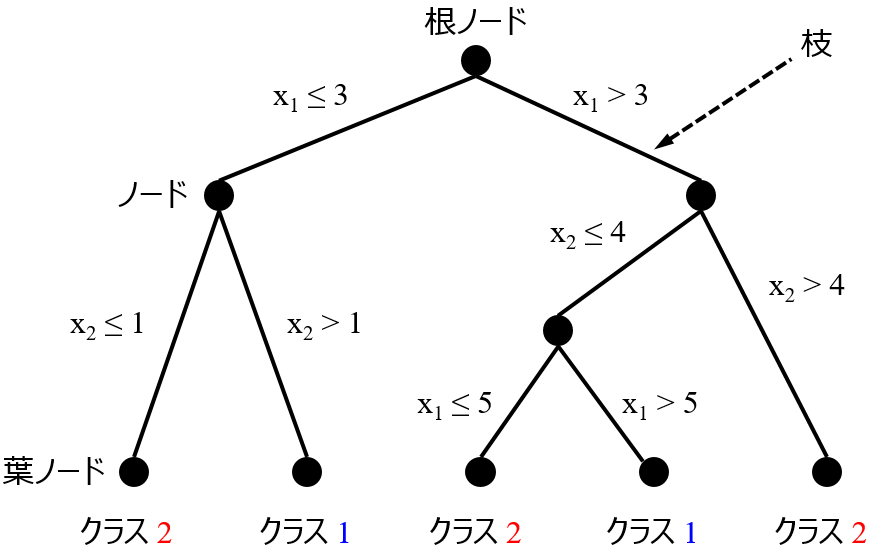
生田:木をたくさん生やして、森 (フォレスト) にする、って感じですね。
応化:その通りですね。もちろん、決定木でなくても、どんな回帰分析手法・クラス分類手法でも、アンサンブル学習できます。
たくさんのモデルの作り方
生田:どうやって複数のモデルを作るんですか?
応化:サンプルや説明変数 (記述子・特徴量・入力変数) を変えてモデルを作ります。
生田:サンプルや説明変数を変える?それぞれ、モデル構築用データとして与えられていますよね?
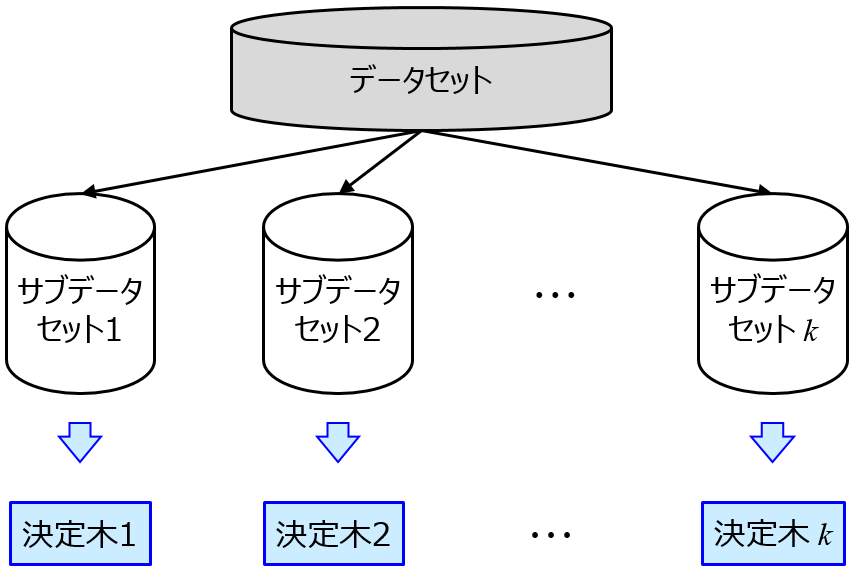
応化:たとえば、モデル構築用データのサンプルから、ランダムにいくつか選んで、新たなデータセットをつくります。これをサブデータセットといいます。サブデータセットごとにモデルをつくるのです。このモデルをサブモデルといいます。
生田:なるほど、100 サンプルからランダムに 90 サンプルを選ぶ、とかですよね。ランダムに選ぶので、サブデータセットごとに 90 サンプルの内容が変わり、その結果として、サブモデル、つまり回帰モデルやクラス分類モデル、が変わるって感じですか。
応化:その通りです。このようにサンプルを選ぶことをリサンプリング (resampling) といいます。リサンプリングのやり方として、
・重複を許してサンプルを選ぶ方法:ブートストラップ法 (bootstrap resampling or bootstrapping)
・重複を許さずサンプルを選ぶ方法:ジャックナイフ法 (Jackknife resampling or jackknifing)
の2つの方法があります。
生田:いくつのサンプルを選べばよいの?ってことはとりあえず置いておいて、重複を許すことについて質問です。重複を許すってことは、A, B, C, D, Eのサンプル5つから3つ選ぶとき、A, A, D とかになる可能性があるってことですか?
応化:そうです。
生田:同じサンプルが2つ以上データセット内にあるのは違和感です。そのようなデータセットで回帰モデルやクラス分類モデルを作るときに問題はないのですか?
応化:気持ちはわかります。ただ、複数回選ばれたサンプルの誤差がより小さくなるよう学習が行われるだけで、学習のときに問題はありません。
生田:それならよかったです。
応化:また、ジャックナイフ法では、先ほどの質問にあった通り、いくつのサンプルを選ぶのか決めなければなりません。しかし、ブートストラップ法では、重複を許してモデル構築用データのサンプル数だけ選ぶのが一般的であり、楽です。
生田:ブートストラップ法では選択するサンプル数を決めなくてもいいんですね。モデル構築用サンプルが100あったとき、その中から重複を許して 100 サンプル選べばよいと。
応化:その通りです。ちなみにこの方法は、bootstrap aggregating の略で、bagging (バギング) と呼ばれています。
生田:へー。
応化:サンプルからではなく、説明変数から選ぶときは、同じ変数があっても無意味なので、ジャックナイフ法を使う必要があります。このときは選択する変数の数を決めなければなりません。
生田:どうやって選べばよいのですか?
応化:たとえば、選択する変数の割合を、10%, 20%, …, 80%, 90% とか変えて、クロスバリデーションをするとよいと思います。クロスバリデーションはこちらをご覧ください。

生田:わかりました!
応化:ちなみに、ランダムフォレストでは、サンプルをブートストラップ法で選び、同時に説明変数をジャックナイフ法で選ぶことで、サブデータセットを作成し、サブモデルとしての決定木をつくっています。わたしは、ランダムフォレストでもクロスバリデーションで選択する変数の割合を決めています。
生田:サブデータセットの数はどうしますか?
応化:多いに越したことはありません。ただ、多いと計算時間がかかるのですよね。わたしの場合、サンプル数が多くて計算時間を待てないときは 100 にしますが、基本的には 1000 にしています。
生田:了解です!サブデータセットごとにサブモデルを作るときは、モデル構築用データで一つのモデルを作るときと同じですか?
応化:はい、同じです。クラス分類モデルでも、回帰分析モデルでも、ハイパーパラメータがあったらクロスバリデーションなどで最適化しましょう。

サブモデルの統合
生田:複数のサブモデルを統合するとき、クラス分類では多数決をしていましたが、回帰分析ではどうしますか?
応化:複数の推定値の平均値にしたり、中央値にしたりします。
生田:中央値のほうがロバストなんですよね?
応化:その通り!
アンサンブル学習のメリット・デメリット
応化:上の図でアンサンブル学習のメリットを説明しましたが、他にもありますので、まとめておきますね。
生田:お願いします。
応化:アンサンブル学習のメリットは下の3つです。
- 外れ値やノイズに対してロバストな推定ができる
- 推定値のバイアスが減る
- 推定値の不確かさ (モデルの適用範囲・適用領域) を考慮できる。
生田:1. は、上の図で説明したやつですか?
応化:その通りです。一つのモデルだと、外れ値やノイズの影響を受けたモデルなので、新しいサンプルの推定のとき、推定を失敗することもあります。アンサンブル学習により、リサンプリングしてたくさんモデルを作ることで、外れ値の影響を受けたサブモデルだけでなく、(あまり)受けていないサブモデルもできるわけで、最後に多数決や平均値・中央値を求めることで、外れ値の影響を減らせます。ノイズについても、推定値が平均化されることでばらつきが軽減できます。外れ値やノイズに対してロバストな推定ができるわけです。ロバストについてはこちらをご覧ください。

生田:2つ目のメリットはどういうことですか?そもそもバイアスって?
応化:バイアスとは、サンプル群の推定値のかたよりのことです。モデルによっては、あるサンプル群で同じような推定誤差があるときがあります。モデルの弱点のような感じです。
生田:一部のサンプルだけうまく推定できないということ?クラス分類でも回帰分析でも?
応化:そうです。アンサンブル学習により、その弱点を補うことができます。ただ、上で説明したバギングでは、残念ながらその効果はありません。
生田:2. のメリットは得られない?
応化:その通りです。アンサンブル学習の中でも、Boosting という手法を使う必要があります。
生田:どんな方法ですか?
応化:たくさんのサブモデルを作るのはこれまでと同じなのですが、新しいサブデータセットを選ぶときに、これまでのサブモデルで推定に失敗したサンプルほど高確率で選ばれるようにします。
生田:そうすることで、弱点のサンプルで学習されたサブモデルが多くなることで、多数決や平均化したときに総合的にも弱点を克服するんですね!
応化:その通りです。Boostingの中で、Adaptive Boosting、略してAdaBoostが有名です。Freund さんと Schapire さんが1995年に発表した方法です。

応化:最後のメリットですが、アンサンブルで推定値の不確かさを考えることができます。
生田:不確かさってどういうことですか?
応化:たとえば、100のサブモデルがあったとき、サンプルaの推定結果として100のサブモデルすべてが + と判定し、サンプルbの推定結果として51のサブモデルが + と判定し49のサブモデルが - と判定することで多数決により + となったとします。サンプルaとbでどっちが + っぽいと思いますか?
生田:100のサブモデルすべてが + と判定したサンプルaの方だと思います。
応化:ですよね。このように、サブモデルの多数決だけでなく、その内訳まで見ることで、不確かさの参考にするわけです。
生田:+ と判定したサブモデルが 70個、- と判定したサブモデルが 30個なので、70%くらいの確率で + ってこと?
応化:そんな感じです。
生田:回帰分析のときはどうするんですか?
応化:そのときは、推定値の標準偏差を指標にします。推定値の標準偏差、つまり推定値のばらつきが小さいときは、平均値・中央値は推定値として確からしいだろう、逆に大きいときはその分 平均値や中央値から実測値がズレる可能性もあるだろう、と考えるわけです。
生田:モデルの適用範囲・適用領域と同じですね。

応化:その通りです!アンサンブル学習で、モデルの適用範囲・適用領域を考慮できるわけです。
生田:3つのメリットはわかりました。デメリットもありますか?
応化:あります。やはり計算時間がかかることです。サブモデルをたくさん構築しなければなりませんし、各サブモデルでハイパーパラメータを最適化しなければなりません。
生田:わかりました!計算時間を考えながら、アンサンブル学習しようと思います!
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。