回帰分析において、新しいサンプルを推定するときの誤差の絶対値の平均値を推定するための指標を開発しました。イメージとしては、テストデータとしてサンプルがたくさんあるときの、モデルの適用範囲 (Applicability Domain, AD) 内のサンプルにおける MAE の値を推定します。

誤差を推定するためのキーワードは yランダマイゼーション (y-randomization, y-scrambling) です。

ちなみにクロスバリデーションは用いません。特にサンプル数が小さいときはクロスバリデーションの結果が不安定になりますし、推定性能を評価したいモデル (テストデータを推定するモデル) とクロスバリデーションにおけるモデルは異なりますしね。
考え方としては、
(新しいサンプルに対する平均的な誤差) = (モデル構築における誤差) + (偶然の相関による誤差)
で計算します。(偶然の相関による誤差) とは、過学習 (オーバーフィッティング) による誤差と言い換えることもできます。めったにありませんが、オーバーフィッティングせず適切にモデル構築できれば、(新しいサンプルに対する平均的な誤差) = (モデル構築における誤差) となります。逆に、ガチガチにオーバーフィッティングして、r2 がほとんど 1 のようなケースでは、(モデル構築における誤差) は非常に小さい (ほぼ 0) ですが、(偶然の相関による誤差) が大きくなり、結果的に (新しいサンプルに対する平均的な誤差) が大きくなります。
では、(モデル構築における誤差) と (偶然の相関による誤差) をどう計算するかです。まず、(モデル構築における誤差) については簡単です。トレーニングデータで回帰モデルを構築し、同じトレーニングデータで計算された MAE (Mean Absolute Error) です。これを MAETRAIN と呼びます。
次に、(偶然の相関による誤差) についてです。はじめに、回帰モデルが完全にオーバーフィッティングしているということは、まったくモデルとして機能していませんので、モデルを構築しないの同じです。このときの誤差を、推定値をトレーニングデータの目的変数の平均値で与えたときの MAE とします。これを MAEMEAN と呼びます。
そして y-randomization を (繰り返し) 行います。y-randomization をしたときの誤差 (MAEyRAND) に関して、偶然の相関の度合いが大きいほど、MAEyRAND は小さくなります。偶然の相関の度合いは小さい方が、新しいサンプルに対する誤差も小さくなるため、MAEyRAND の分だけ新しいサンプルに対する誤差が小さくなると考えます。
以上をまとめると、(新しいサンプルに対する平均的な誤差) を推定する指標 Chance Correlation‐Excluded Mean Absolute Error (MAECCE) は下図のようになります。
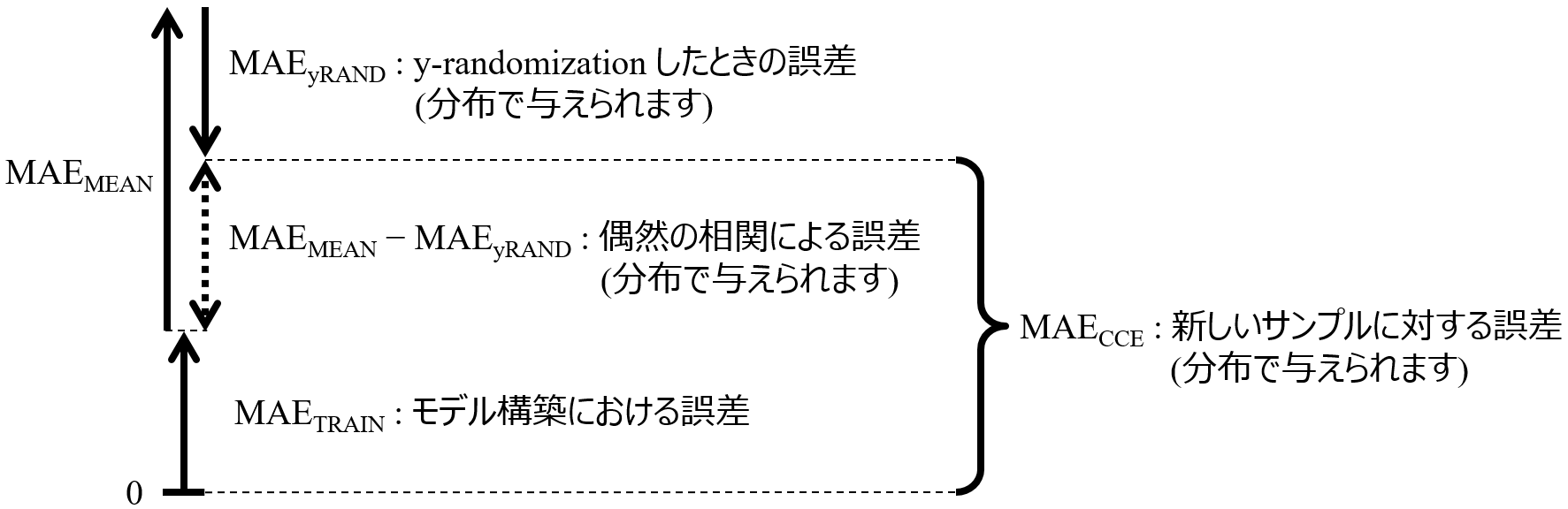
式で表すと
MAECCE = MAETRAIN + MAEMEAN − MAEyRAND
となります。y-randomization は繰り返し行われることから、MAEyRAND は分布で与えられ、それにより MAECCE も分布で与えられます。新しいサンプルに対する平均的な誤差は MAECCE の分布内にあるだろう、というわけです。
論文では、数値シミュレーションデータセットや実際のデータセットを用いて、MAECCE によりテストデータの MAE を推定できることを検証しています。線形の回帰分析手法、非線形の回帰分析手法だけでなく、LASSO や GAPLS, GASVR といった変数選択をする場合にも、MAECCE が機能することを確認しています。
MAECCE は、AD を設定してサンプルごとの誤差のばらつきを推定するときのベースにも使えると考えています。
論文はこちら https://onlinelibrary.wiley.com/doi/10.1002/cem.3171 から読むことができます。また、こちらの DCEKit で、便利に MAECCE をご利用いただけます。

もし興味がありましたらよろしくお願いいたします。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。

