適応的実験計画法により、高機能性材料を達成するための実験条件・製造条件を探索したり、高性能プロセスを開発するためのプロセス条件を探索したりするとき、ベイズ最適化を用いることで効率的に外挿を探索しながら目標達成を目指すことができます。設計問題においては、目的変数 Y が複数あるときもあります。すべての Y が目標を達成する材料やプロセスを開発するため、Y をすべて考慮してベイズ最適化の獲得関数とする方法について紹介しました。

Probability of Improvement (PI) は Y ごとに、現状の Y のデータから向上する「確率」として表現されるため、Y 同士で確率の掛け算をするだけで、それらを同時に達成する確率と定義でき、複数の Y があっても対応できます。さらに、Y においては目標範囲があるときもあり、そのような Y においても PI と似た計算で目標範囲を達成する「確率」とすることができるため、最大化を目指す Y、最小化を目指す Y、目標範囲のある Y が混在していても、それらを統合して一つの獲得関数 (すべての Y が良好になる確率) にできます。その確率が高いサンプル、実際には対数変換して足し合わせた指標が大きいサンプルを探索することになります。
では、Expected Improvement (EI) や Mutual Information (MI) などの他の獲得関数では、Y が複数あったときに対応できないのでしょうか。PI や目標範囲を達成する確率は、確率という表現方法から統合しやすいため、わたしもよく使っていますが、他の獲得関数でも工夫すれば複数の Y があるときにも対応できます。
ちなみに、基本的に Y ごとにガウス過程回帰モデルを構築しており、上で述べた確率を統合する方法や、これからご紹介する方法に関しては Y の相関関係は考慮していません。ただ、ベイズ最適化では外挿を効率的に探索することになり、今あるデータセット内での Y の相関関係が、外挿領域でどうなっているかはわかりません。そのため基本的には Y の相関関係までは考慮しなくてよいと考えています。なお Y の相関関係を考慮したい場合は Gaussian Mixture Regression (GMR) を用いるのがよいです。
EI や MI などの Y のスケールに依存する獲得関数では、Y ごとの獲得関数を単純に統合することはできません。そのため、一つの方法として、各 Y で獲得関数を計算してから、それらのパレート最適解を考えることはあります。パレート最適解に関してはこちらをご覧ください。
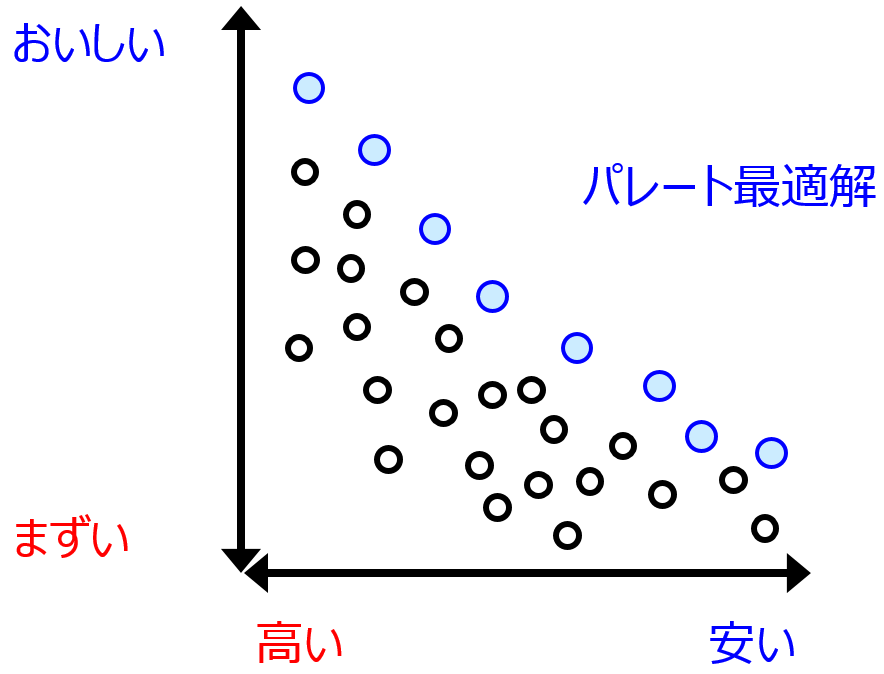
あるサンプルについて、すべての Y において獲得関数の大きい別のサンプルがあるとき、そのサンプルはパレート最適解ではありません。パレート最適解ではないサンプルをすべて除いたとき、残ったサンプルがパレート最適解です。パレート最適解のサンプルの中から、実際に実験したり製造したりシミュレーションしたりするサンプルを選択することになります。
もう一つのやり方は、一つの指標に落とし込む方法です。Y ごとに獲得関数を計算した後に、獲得関数ごとに、トレーニングデータにおける獲得関数の平均値と標準偏差を用いて (新しいサンプルにおける平均値や標準偏差ではありませんのでご注意ください)、新しいサンプルの獲得関数を標準化 (オートスケーリング) します。

これにより、すべての Y の獲得関数が同じスケールになります。標準化後、すべての獲得関数の和を取り、一つの指標とします。この指標の値が大きい順にサンプルを並び替えて、順番にチェックすると効率的になります。単純にすべての獲得関数の和を取るのではなく、Y の重要度に応じて獲得関数ごとに重みを付けて足し合わせてもよいかもしれません。
以上のようにして、色々な獲得関数でも複数の Y があるときに対応でき、すべての Y が良好になるように探索するベイズ最適化が可能になります。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


