金子研の論文が Materials & Design に掲載されましたので、ご紹介します。タイトルは
です。これは修士卒の清水直斗さんが修士二年生のときに取り組んだ研究の成果です。
高機能性材料の研究や開発において、新たな材料や化合物は、複数の物性もしくは活性などの目標値を達成する必要があります。既存のデータセットを用いて、物性や活性 Y と特徴量 X との間で回帰モデルを構築するとき、Y ごとに一つ一つ回帰モデルを構築する方法では、Y 同士の関係を考慮することができません。そのため、すべての Y が条件を満たす候補を、効率的に探索することが難しいです。
さらに、一般的に行われているモデルの逆解析の方法は擬似的な逆解析であり、X の多数の候補を生成し、それらを回帰モデルに入力して得られる Y の予測値 (ベイズ最適化であれば獲得関数の値) に基づいて候補を選択します。

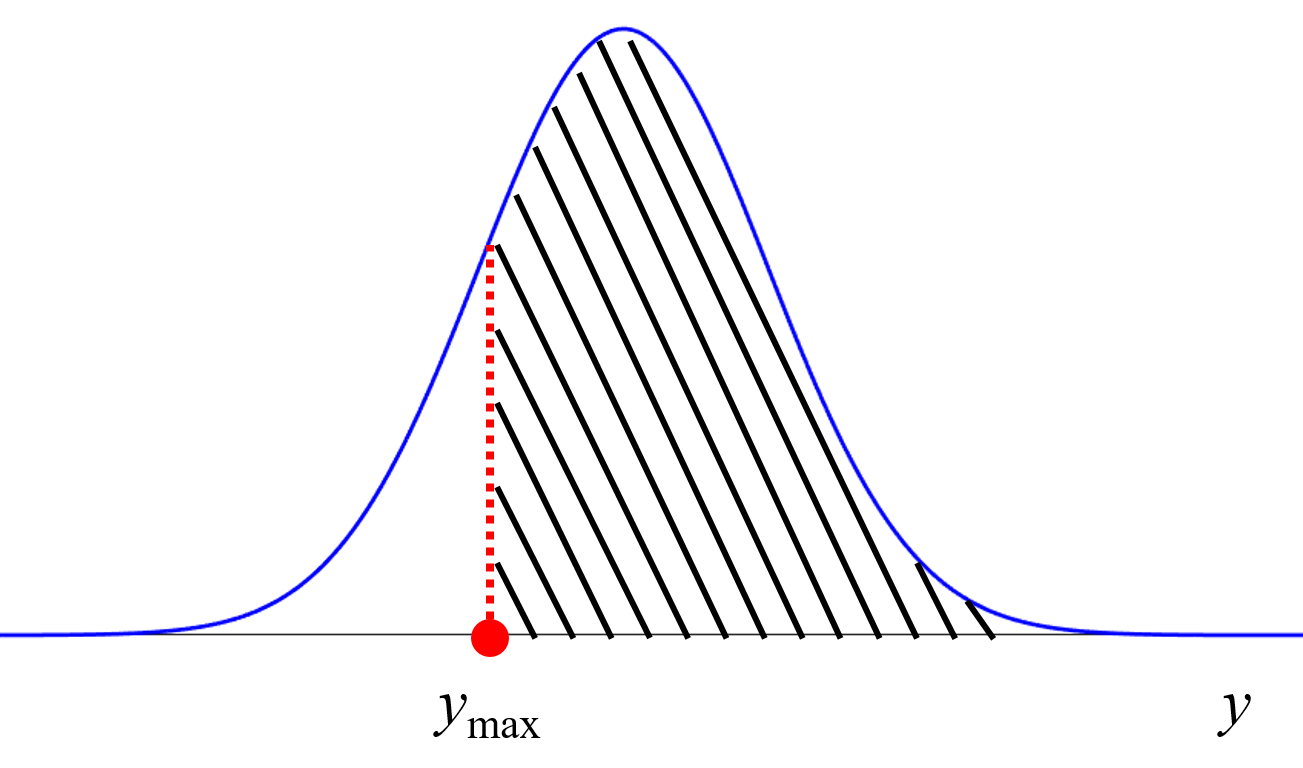
この方法では、無限ともいえる実験条件の候補や化学構造の中から、所望の物性値や活性値をもつものを探索することは難しいです。
そこで今回は、X を入力することで複数の Y を同時に出力できる手法の 1 つである、Gaussian Mixture Regression (GMR) に着目しました。
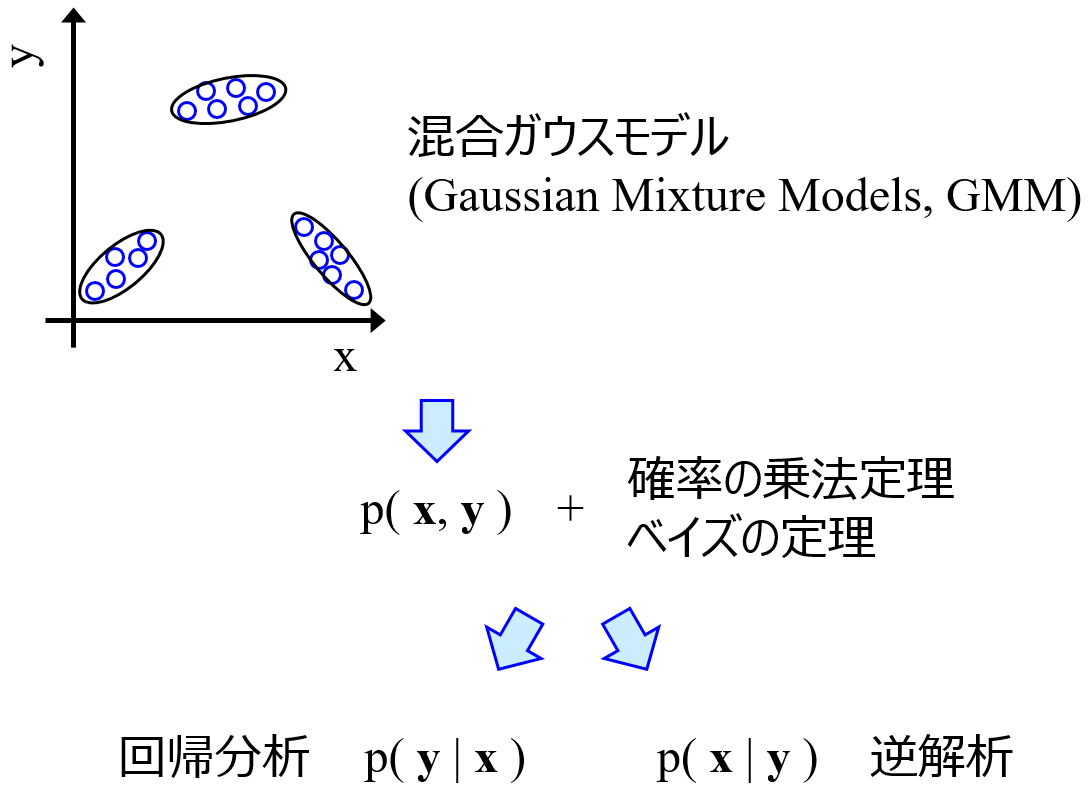
GMR は、Y 同士の関係を考慮しながら複数の Y を同時に予測できるだけでなく、Y を入力して直接的に X を予測できることから、所望の物性・活性の組合せをモデルに入力することで、それを満たす X の候補を直接得ることが可能となります。
この論文では、Y 同士に非線形の相関があり、X と Y の間にも非線形の相関があるシミュレーションデータを作成し、GMRモデルの予測精度とGMRモデルを用いた逆解析の性能を検討しました。その結果、Y が複数ある場合において、サポートベクター回帰 (Support Vector Regression, SVR) と比較し、適切に Y の外挿領域を探索でき、シミュレーションによって結果の再現性も精度よく得られることが確認されました。
さらに、熱電変換材料の性能物性データを解析し、新規高性能熱電変換材料の候補を探索しました。実際の材料データでは、実験できなかったため再現性の確認は取れておりませんが、GMR により Y が複数ある場合においても効果的に逆解析できることも検証されています。
内容の詳細は論文をご覧いただけますと幸いです。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。