既存のデータセットを用いて、説明変数 x と目的変数 y の間で、回帰分析手法やクラス分類手法により、モデル y = f(x) を構築したり、構築したモデルを用いて、望ましい y の結果になるように x の値を設計したりします。予測精度の高いモデル、すなわち y の値が未知のサンプルに対して、x の値から正確に y の値を予測できるモデルが望まれますので、もちろん回帰分析手法やクラス分類手法について工夫することもありますが、y を説明しやすい x を設計することも重要といえます。いわゆる特徴量設計や特徴量エンジニアリングと呼ばれるものです。
ただ、もちろんモデルの予測精度も重要ですが、モデルを構築した後にそのモデルの逆解析、すなわち y の値から x の値を設計することを行うとき、x として用いることのできる特徴量に制限があります。
わかりやすい例でいえば、x はすべて、実験条件、合成条件、製造条件、評価条件、シミュレーション条件のように、実験のため、合成のため、製造のため、評価のため、シミュレーションのための、何らかの条件である必要があります。例えば (途中結果でも) 実験結果やシミュレーション結果の情報は使用できません。なぜなら、逆解析して x の値を提案した後、何らかの条件であれば、その設計された値で次の実験やシミュレーションができますが、実験結果の x のように成り行きの値として変わるものでは、設計された値になるようにコントロールすることが難しいためです。ただし、条件でなくても、実験中やシミュレーション中に、コントロールできるような量であれば x として用いることができます。
また、他の制限の理由を説明するため、少し丁寧に特徴量エンジニアリングとモデルの逆解析の関係についてお話ししますと、まずモデルの逆解析では、y の値が望ましい値となるような、実験条件、合成条件、製造条件、シミュレーション条件のような設計変数の値を決めることになります。もちろん設計変数を x として用いて、y = f(x) のモデルを構築してもよいですが、モデルの予測精度を上げるために、特徴量エンジニアリングをして設計変数を別の特徴量に変換して x としたり、元の設計変数と変換した特徴量をあわせて x としたりします。モデル y = f(x) を構築し、その逆解析によって、x の値を設計できたとしても、求めたいのは設計変数の値であり、設計変数の値が得られないと意味がありません。一般的な逆解析では、設計変数の大量の候補を生成して、それらの y の値を予測し、予測結果が良好な設計変数の値を選択します (ベイズ最適化では、獲得関数の値が良好な設計変数の値を選択します)。y の値を予測するためには、設計変数から x を一意に計算できないといけません。そのため、特徴量エンジニアリングして得られた x に制限があるのです。
以上のことから、x として用いるためには、設計変数から一意に計算できなければいけません。例えば主成分分析 (PCA)、tSNE、UMAP、オートエンコーダ (AE) のように、設計変数から潜在変数にすることも特徴量エンジニアリングとしたとき、PCA、UMAP、AE を用いることはできますが、tSNE を用いることはできません。tSNE は与えられたデータセットを潜在変数に変換するだけなので、新たなサンプルを入力して潜在変数の値を計算するといったことができないためです。
GMR, VBGMR や GTMR により、
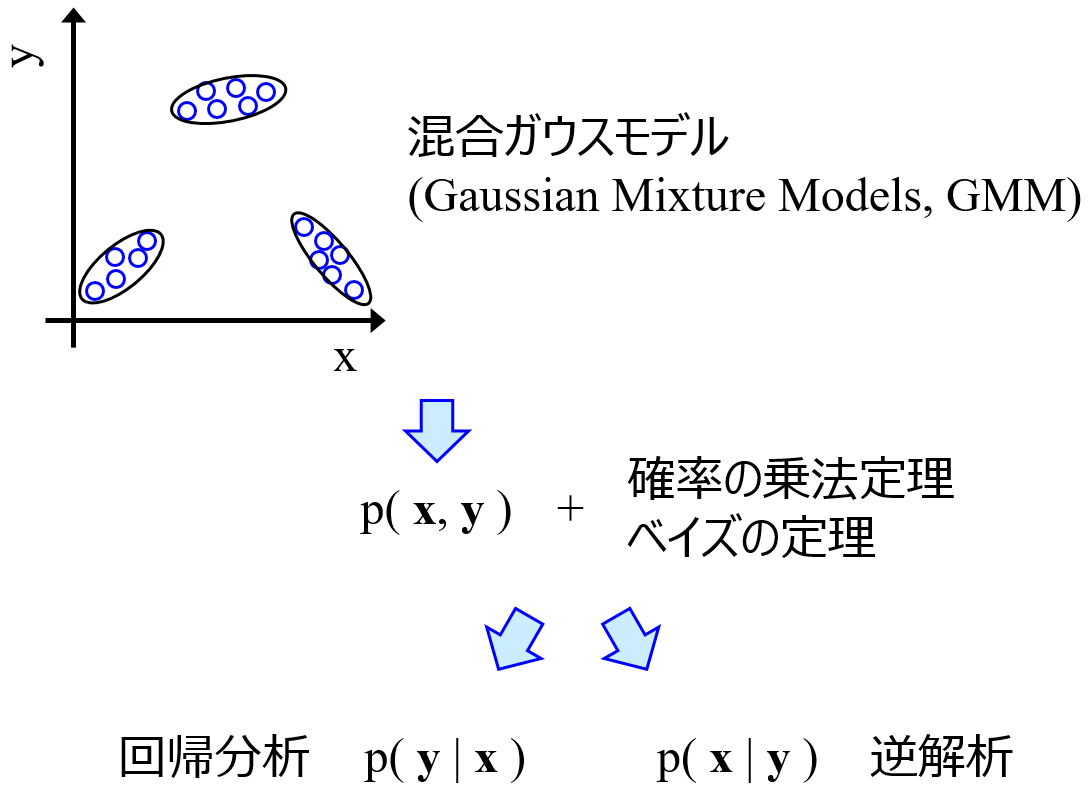


直接的逆解析をするには、さらなる制限があります。なぜなら、一般的な逆解析では、大量に x の候補を生成し、それらすべての y の値を予測し (ベイズ最適化では獲得関数の値を計算し)、良好な結果を選択する、といったことをしますが、直接的逆解析では、y の目標値から直接的に x の値を計算します。そのため (設計変数から x ではなく) x から設計変数を計算できる必要があります。先の例で言えば、PCA や AE を用いることはできますが、tSNE や UMAP を用いることはできません。
今回は分かりやすさのため PCA、tSNE、UMAP、AE といった潜在変数を計算する手法で説明しましたが、解析者・実験科学者の知識・知見・経験・感性などによって特徴量を設計するときにも同様に、モデルの逆解析をする際の特徴量エンジニアリングには注意が必要です。ご注意ください。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


