低次元化を駆使して直接的逆解析法の予測精度を向上させる手法を開発しました！[金子研論文]

金子研の論文が Chemometrics and Intelligent Laboratory Systems に掲載されましたので、ご紹介します。タイトルは

Lifting the Limitations of Gaussian Mixture Regression through Coupling with Principal Component Analysis and Deep Autoencoding

です。

説明変数 x のサンプルを大量に生成してから目的変数 y を予測し、ベイズ最適化の文脈では y の予測時の分散も計算して獲得関数を求め、予測値や獲得関数の値が良好な x のサンプルを選択する擬似的な逆解析とは異なり、y の目標値から直接的に x の値を予測する直接的逆解析法におけるお話です。

Gaussian Mixture Regression (GMR) や Generative Topographic Mapping Regression (GTMR) によって直接的逆解析ができるようになり、

[Pythonコードあり] 教師あり混合ガウスモデル(Supervised Gaussian Mixture Models)で回帰分析も逆解析も自由自在に♪～Gaussian Mixture Regression(GMR)～

混合ガウスモデル (Gaussian Mixture Models, GMM) を教師あり学習に対応させた Gaussian Mixture Regression (GMR) について、pdfとパワーポイントの資料を作成しました。GMM に...

Generative Topographic Mapping(GTM)でデータの可視化・回帰分析・モデルの適用範囲・モデルの逆解析を一緒に実行する方法 [金子研論文]

今回は、Generative Topographic Mapping (GTM) でデータの可視化・回帰分析・モデルの適用範囲・モデルの逆解析を一緒に実行できる手法を開発し、QSPR 解析・QSAR 解析と分子設計を行った論文が、molec...

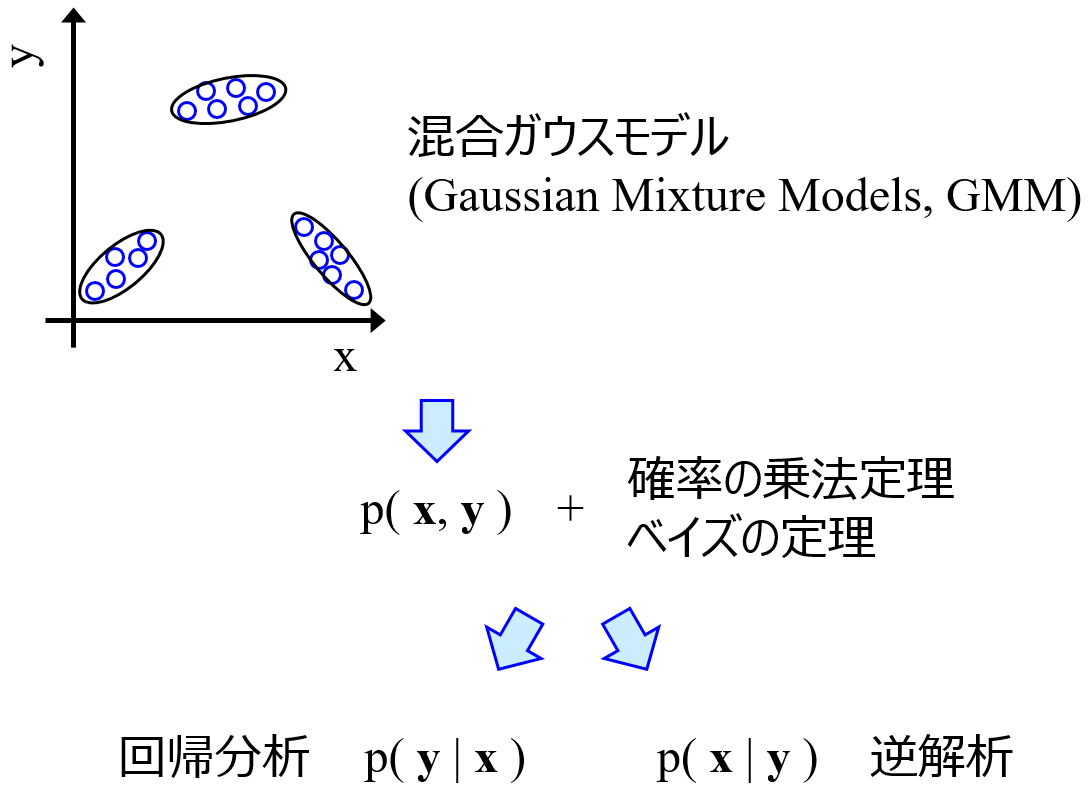
それぞれ y と x を含むすべての変数間の関係をモデル化します。具体的には、すべての変数間の関係を正規分布の重ね合わせ、つまり混合正規分布と仮定し、混合正規分布のパラメータを最適化します。このようにすべての変数間の関係を求めることから、変数の数が大きくなると計算時間も増大しますし、モデル化するのも困難になる、すなわち予測精度が低下する傾向があります。

そこでこの論文では、直接的逆解析法の予測精度向上のため、低次元化手法と直接的逆解析法を組み合わせた手法を開発しました。x と y を合わせてモデル化するのではなく、x から低次元化した潜在変数 z と y を合わせてモデル化します。

ただ低次元化といっても、いわゆる低次元化手法のすべてを使用できるわけではありません。直接的逆解析を達成するためには、y の値から z の値を計算した後に z から x に変換できる、すなわち x から z への変換だけでなく、z から x への逆変換も行える必要があります。そこで今回は主成分分析 (Principal Component Analysis, PCA) とディープオートエンコーダ (Deap AutoEncoder, DAE) を採用しました。PCA や DAE であれば、モデルを構築した後に、x から z の変換だけでなく、z から x の変換もできるようになり、x → z → y の順解析や、y → z → x の逆解析も達成できます。さらに DAE であれば x 間の非線形関係も考慮した上で、z に変換できます。

PCA の主成分の数や、DAE のネットワーク構成は、クロスバリデーションで最適化されます。

実際の分子のデータセットや材料のデータセットやスペクトルのデータセットといった様々なデータセットを用いて、提案手法の予測精度を検証したところ、すべてのデータセットにおいて従来手法と比べて予測精度が向上し、最大で予測誤差の 63 % も低下することを確認しました。

興味のある方は、ぜひ論文をご覧いただければと思います。どうぞよろしくお願いいたします。

以上です。

質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。