分子設計・材料設計・プロセス設計において、分子記述子や合成条件・製造条件やプロセス条件などの説明変数 x と材料の物性・活性・特性などの目的変数 y との間で数理モデル y = f(x) を構築して、そのモデルを用いて x の値から y の値を予測したり、y の値が所望の値になる x の値を設計したりします。
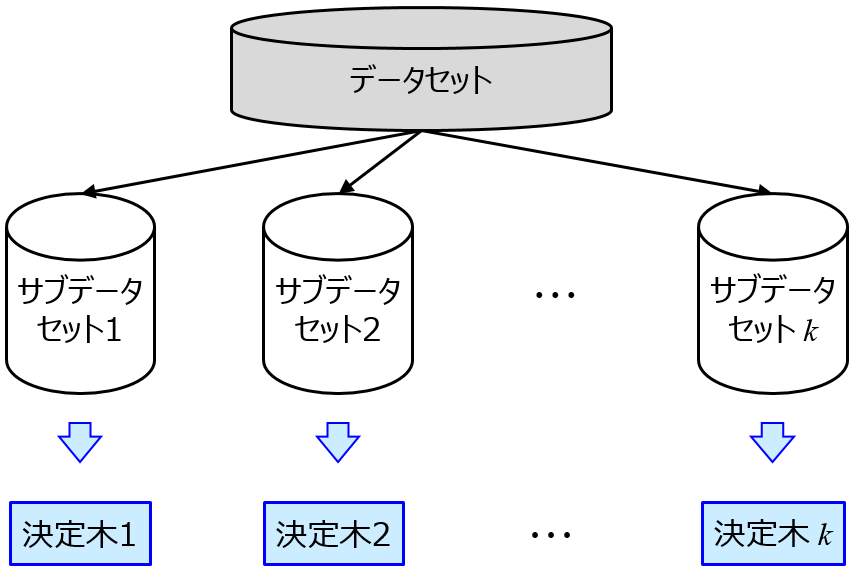
特に x と y の間の関係性を解明したいとき、特徴量の重要度を計算することがあります。例えば決定木に基づくアンサンブル学習を使用した手法であるランダムフォレスト、Adaboost、勾配ブースティング、XGBoost、LightGBM などでは、特徴量の重要度を計算できる機能が手法内にあり、モデルを構築するときに特徴量の重要度を計算できます。


モデルの予測精度を評価するときに、トレーニングデータでモデルを構築してテストデータの y を予測してみて、テストデータの y をどれくらい予測できたか評価したり、ダブルクロスバリデーションでモデルの予測精度を評価したりします。


特徴量の重要度は、モデルの予測精度によらず計算できますが、モデルの予測精度が低いとき、例えばテストデータの y の予測誤差が大きかったり、ダブルクロスバリデーション後の y の予測値と y の実測値とが全然合わなかったりしたときに、(トレーニングデータの y の計算値と y の実測値が非常によく合っているとはいえ) 特徴量の重要度を信用してよいのでしょうか?
結論としては、そのようなモデルの予測精度が低いときに特徴量の重要度を信用してはいけません。
この理由を理解するためには、実際に追加のデータ解析をするのがよいでしょう。そのデータ解析では乱数をうまく使います。

まず、データセットにおける x の数と同じ数だけ、乱数を用いて x のデータセットを生成したり、元の x のデータセットにおける x ごとにサンプルの値をシャッフルしたりして無意味なデータセットを作ります。次に元の x のデータセットとつなげます。x の数が 2 倍になります。そして、x の数が 2 倍になったデータセットで特徴量の重要度を計算します。
特にモデルの予測精度が低いときには、オリジナルの x の重要度と同じくらい、乱数に基づく x の重要度が高くなってしまいます。乱数に基づく x はまったく無意味な特徴量であり、その重要度と同じくらいの重要度であるということは、まったく無意味な特徴量の重要度と同程度ということであり、このような場合には特徴量の重要は意味をなさないことが理解できると思います。
もちろんモデルの予測精度は高いか低いか、二つのどちらかで判断できるものではなく、その間のグラデーションの中にモデルの予測精度があります。どの場合に特徴量の重要度を信用できるかは、モデルの予測精度だけでは判断できないところがあります。そのため不安な方は、上で述べた方法、つまり乱数に基づいて x のデータセットを生成して元の x のデータセットとつなげて特徴量の重要度を計算することで、オリジナルの x の重要度をどれくらい信用できるのか議論するとよいでしょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


