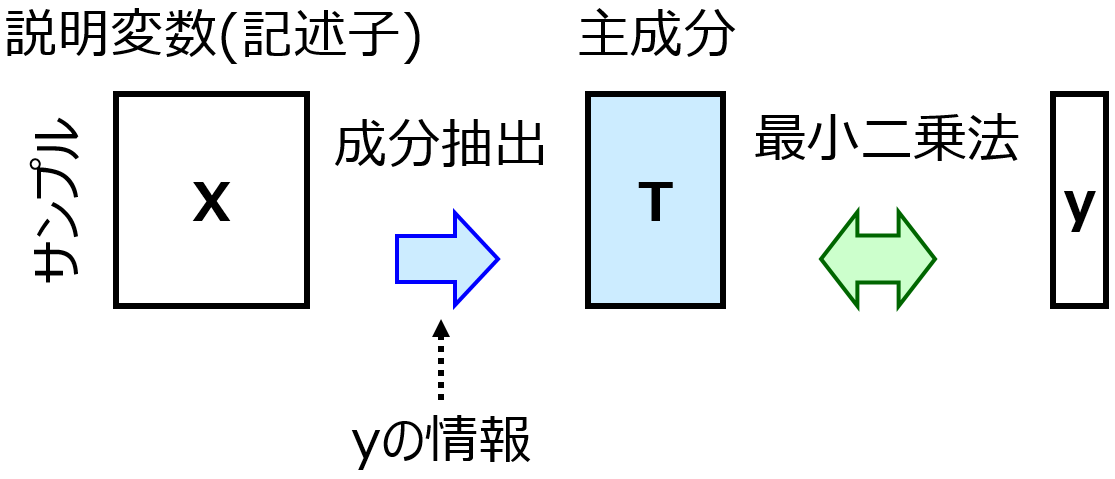
分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築し、構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。
予測精度の高いモデルを構築するため、そしてモデルの解釈性を向上させるため、特徴量選択・変数選択を行うことがあります。今回はその中で、遺伝的アルゴリズム (Genetic Algorithm, GA) を用いた変数選択についてです。
GA と回帰分析手法を組み合わせることで、その回帰分析手法で構築されるモデルにおける予測精度の指標の値が大きくなるように、x の組み合わせを決められます。


例えば GA とガウス過程回帰 (Gaussian Process Regression, GPR) を組み合わせた GA-GPR では、GA の適合度 (目的関数) を GPR を用いてクロスバリデーションを行ったときの、回帰分析では r2 など、クラス分類では正解率などとすることで、r2 や正解率が大きくなるような x の組み合わせを求められます。適合度の計算において、クロスバリデーションによる評価の代わりに、テストデータを用いた評価にしても構いません。他にも、例えば GA-PLS や GA-SVR では上の GPR がそれぞれ PLS や SVR になります。

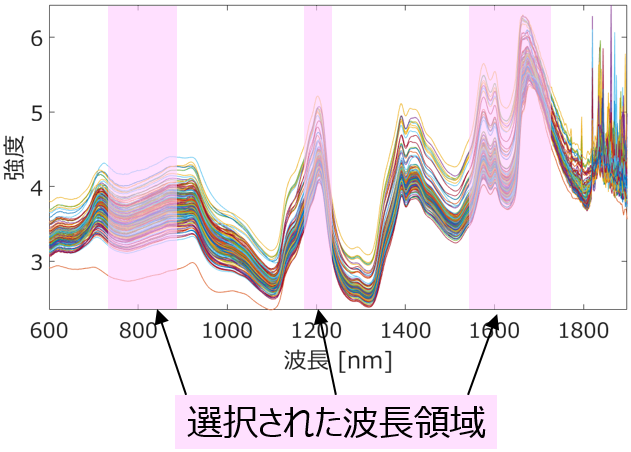
Genetic Algorithm-based WaveLength Selection (GAWLS) や Genetic Algorithm-based process Variable and Dynamics Selection (GAVDS) を用いることで、それぞれスペクトルデータにおいて波長の領域や波数の領域を幅で選択できたり、時系列データにおいてプロセス変数とその時間遅れを同時に選択できたりします。
これらの GA を用いた特徴量選択の問題は、過学習を起こしやすいことです。

本来であれば y とは関係のない x にもかかわらず、(他の x との関係性を含めた) 偶然の相関によって、無意味な変数でも選択されてしまいます。

これは特にサンプルが少ないときに起こりやすく、GA の適合度の計算において、クロスバリデーションからテストデータの r2 や正解率に変えても、偶然の相関や過学習が起こる可能性はゼロにはなりません。言い換えると、yランダマイゼーションをしたときも、クロスバリデーション後やテストデータにおける r2 や正解率が大きくなってしまいます。
偶然の相関の影響を低減させる一つの方法は、ドメイン知識などで、選択される特徴量に制約を設けることです。例えば、ある特徴量 A が選択されるときには時には特徴量 B は選択されないとか、特徴量 C が選択されるときは必ず特徴量 D が選択されるとかです。GAWLS によるスペクトル解析でも、例えばある波長もしくは波数は必ず選択されるような領域にするとか、GAVDS においても、例えばあるプロセス変数 F の時間遅れは、別のプロセス変数 G の時間遅れよりも大きくなるようにするとかです。
このように制約を設けることで、特徴量選択の自由度が下がり、偶然の相関が起こりにくくなります。もちろん可能性がゼロになるわけではありませんので、yランダマイゼーションでも検証する必要があると思いますが、制約を設けない場合と比べると、本来のデータセットにおける r2 や正解率と、yランダマイゼーション後の r2 や正解率との差が大きくなる傾向になります。
GA を用いた特徴量選択、波長(波数)領域選択、プロセス変数とその時間遅れの同時選択を検討するときは、上のような制約をできる限り考慮するようにしましょう。
以上です。
質問やコメントなどありましたら、X, facebook, メールなどでご連絡いただけるとうれしいです。


