いろいろなデータセットを解析する上で、データ解析の基本的な流れを整理しておきます。ここでは、回帰分析やクラス分類をするときにように、教師ありのデータセット、つまり目的変数 Y があるようなデータセットを解析することを想定しています。流れにおける、いろいろなデータ解析の手法の詳細についてはこちらをご覧ください。

まずはデータセットの前処理をします。たとえば、数字の入っていない変数 (特徴量・記述子) を削除したり、標準偏差が 0 の変数を削除したり、相関係数の絶対値の大きい変数を削除したり、といった感じです。ちなみに、相関係数の大きい変数を削除するプログラムはこちらに公開しております。

もし必要であればご覧ください。
次に、データセットを把握することを試みます。たとえば、変数の数やサンプルの数を確認したり、Y のヒストグラムを確認したり、Y と説明変数 X の各変数との間で相関係数を計算して、そのヒストグラムを確認したり、その相関係数の絶対値が大きい X の変数を選んで、Y との散布図を確認したり、です。他の X の変数と Y との散布図を確認したり、X の変数間の相関係数や散布図を確認したり、他にも確認したい情報があったら確認してみましょう。
続いて、サンプルのデータ分布を確認します。変数の数が 4 つ以上あるような多変量のデータセットでは、そのままではサンプルのデータ分布を確認することはできませんので、主成分分析

などの低次元化手法・可視化手法を用います。非線形の低次元化手法・可視化手法では、GTM・t-SNE などがあります。
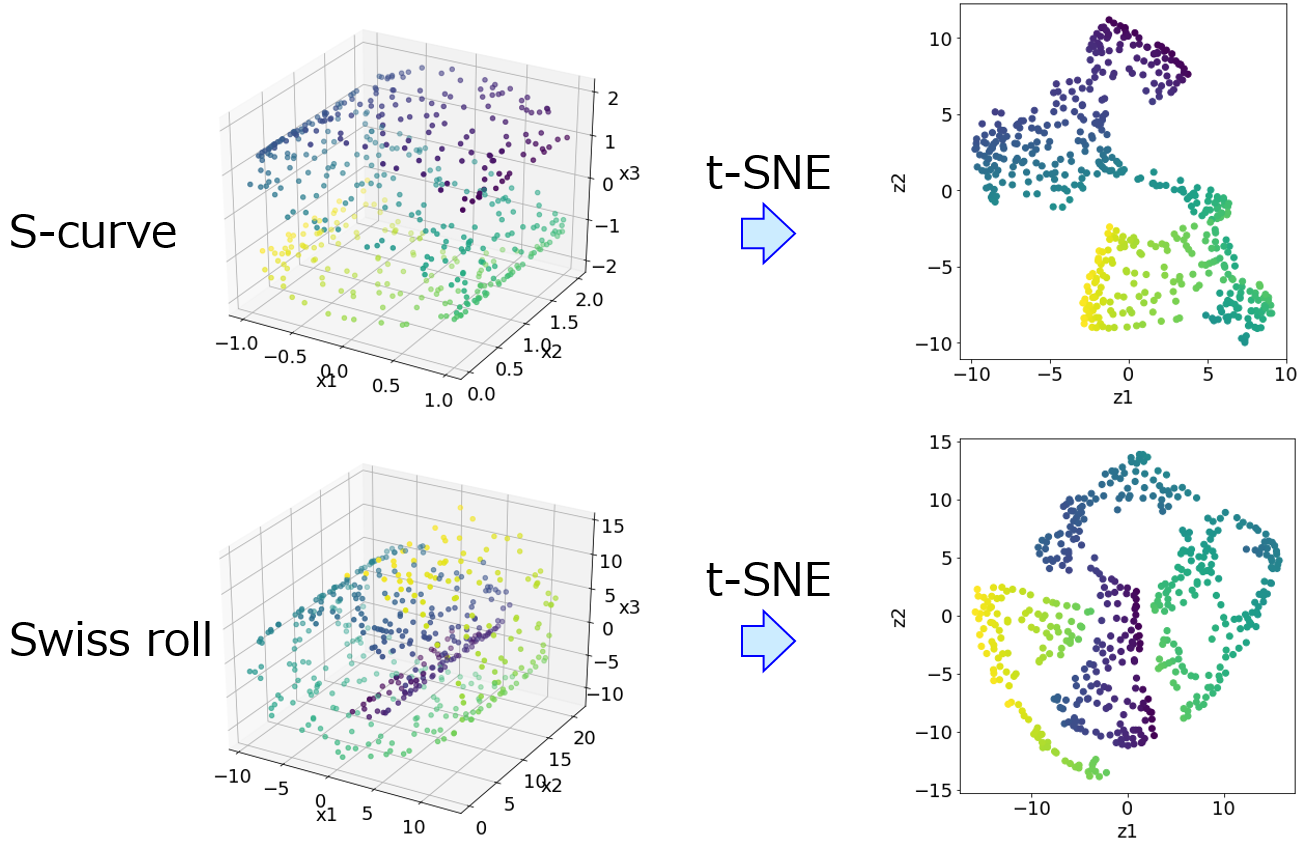
いずれにせよ、これらの手法によってサンプルのデータ分布を確認します。
もちろん、たとえば主成分分析における各主成分の寄与率が低い場合には、いくつかの主成分のプロットを確認した方がよいです。ただそれでも、実際の変数 (特徴量・記述子) の空間におけるサンプル同士の近接関係 (どのサンプルとどのサンプルが近い、といった関係) と、可視化した後の平面におけるサンプル同士の近接関係とは異なります。
そこで、クラスタリングによって、実際の変数 (特徴量・記述子) の空間において近いサンプルの情報も確認するとよいでしょう。たとえば階層的クラスタリングのあとの樹形図 (デンドログラム) を確認したり、クラスターの数を決めて、そのクラスター内のサンプルを確認したりします。
その後、Y の値やクラスを使って、回帰分析やクラス分類を行います。回帰分析やクラス分類の目的は、新しい (Y の値が不明な) サンプルにおける、Y の値やクラスを正確に推定することです。その目的を達成できるかどうか検証するため、回帰モデルやクラス分類モデルの構築に用いないサンプルを、あらかじめ準備しておく必要があります。モデルを構築するサンプルのことをトレーニングデータと呼び、構築されたモデルを検証するためのサンプルをテストデータと呼びます。トレーニングデータを用いて、回帰モデルやクラス分類モデルを構築するわけですが、回帰分析手法やプラス分類手法によっては、モデルを構築する前に決めておくべきパラメータであるハイパーパラメータがあります。このハイパーパラメータの最適化には、クロスバリデーションが用いられます。

回帰分析手法やクラス分類手法ごとに、クロスバリデーションでハイパーパラメータを決めて、トレーニングデータを用いてモデルを構築するわけです。構築されたモデルを用いてテストデータにおける Y の値やクラスを推定して、手法ごとにテストデータの Y の値やクラスをどの程度推定できたか、比較検討します。
ここで、トレーニングデータとテストデータとにサンプルを分割するほど、元々のサンプルがない場合を考えます。このような場合では、テストデータの推定結果で各手法によって構築されたモデルの推定性能を比較検討するかわりに、ダブルクロスバリデーションによって、各手法を比較検討するとよいでしょう。

各手法によって構築されたモデルの推定性能を、トレーニングデータとテストデータとに分けて検証する場合でも、ダブルクロスバリデーションによって検証する場合でも、回帰分析手法やクラス分類手法ごとの推定性能を評価してそれらの手法を比較します。基本的には、この過程の比較検討により、最も推定性能の高い回帰分析手法やクラス分類手法を選択します。
回帰分析手法やクラス分類手法が決定したら、これまでトレーニングデータとテストデータに分けていたサンプルを統合したすべてのサンプルを用いて、選択された手法により、改めて回帰モデルやクラス分類モデルを構築します。もちろん手法によってはハイパーパラメータがありますので、ここでも改めて、全てのサンプルを用いたクロスバリデーションにより、ハイパーパラメータの値を最適化します。
最適化されたハイパーパラメータを用いて、すべてのサンプルで構築されたモデルが最終的に用いられるモデルです。Y の値やクラスが不明な、新たなサンプルを入力して Y の値やクラスを推定したり、Y の値が目標の値になるような X の候補を設計したりします。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。