データは、基本的に下図のように多次元で表現されていますので、
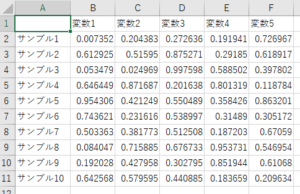
(次元の数は、変数の数とお考えください。厳密には異なりますが、だいたい同じです。)
工夫をしないとデータセットの全体像を見ることはできません。
下図のように、多次元空間に存在するサンプル (左) を2次元に変換する (右) 手法はたくさんあります。
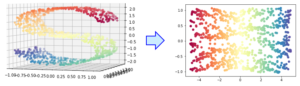
(上の例では多次元といっても3次元なので、左の図でも全体像を見ることができますが、4次元以上になると見るのは難しいです。)
今回は、そんなデータの可視化・見える化のための手法を選ぶときのポイントを押さえておきます。
サンプルの近接関係は、多次元空間⇔2次元平面 で保持されているか?
多次元空間にあるサンプルを、適当に2次元平面に置いたのでは、データの可視化・見える化は まったく意味がありません。実際の多次元空間にあるサンプルたちの様子と近いものを、2次元平面で見たいわけです。
そこで考えるべきなのは、
① 多次元空間において近いところにあるサンプル同士は、2次元平面においても近いか?
② 2次元平面において近いところにあるサンプル同士は、多次元空間においても近いか?
です。
たとえば主成分分析(Principal Component Analysis, PCA)は、①を満たしています。PCAは線形の手法であり、硬い板のような曲がらない平面を多次元空間におき、そこにサンプルを射影しているようなものです。そのため、多次元空間において近い位置関係にあるサンプル同士は、2次元平面においても近いところにあります。
ただPCAは②は満たしません。つまり、2次元平面においてサンプル同士が近くても、多次元空間においては遠い可能性があります。PCAを用いた可視化の結果を見るときには注意が必要です。もちろん、多次元空間におけるサンプル同士の距離を見たり、PCAモデルの残差を見たりすることで検討もできます。
②を満たすのは、自己組織化マップ (Self-Organizing Map, SOM) の上位互換である Generative Topographic Mapping (GTM) です。GTMは非線形の手法であり、ゴム状のシートを曲げたり伸び縮みさせたりしながら、多次元空間にあるサンプルを通るようにシートを置き、そのシートにサンプルを射影するような手法です。そのため、GTMの2次元平面において近いサンプル同士は、多次元空間においても近い位置にあるといえます。
ただGTMでも①は満たしません。つまり、多次元空間において近いサンプル同士であっても、2次元平面上では遠い位置にあることがあります。GTMによって可視化した結果を見るときには注意しなければなりません。
ちなみにSOMは①も②も満たしません。また、
③ 多次元空間において遠いところにあるサンプル同士は、2次元平面においても遠いか?
④ 2次元平面において遠いところにあるサンプル同士は、多次元空間においても遠いか?
も大事ですが、③は②の、④は①の対偶ですので、①と②のみ検討すれば十分です。
いくつかの可視化手法を整理します。
①を満たすもの
- Principal Component Analysis (PCA)
- Kernel PCA
- Factor Analysis (FA)
- Multi-Dimensional Scaling (MDS)
- Isometric feature mapping (Isomap)
②を満たすもの
- Generative Topographic Mapping (GTM)
その他
Locally Linear Embedding (LLE) は、多次元空間にある各サンプルが、それぞれ近いいくつかのサンプルの線形結合で与えられることを仮定します。そしてその線形結合の関係が2次元平面でも成り立つように可視化が行われます。サンプル同士の距離は見ていないため、①も②も必ず満たすとはいえませんが、サンプルの位置関係は、多次元空間⇔2次元平面 で保持されます。
t-distributed Stochastic Neighbor Embedding (tSNE) は、これも①も②も必ず満たすとはいえません。しかし、①と②とを同時に満たす方向を与えてくれる関数が陽に与えられており、その関数を最大化することで可視化します。①も②も満たす保証はありませんが、それらを同時に満たす可能性があるという点で、面白い手法です。
SOMは①も②も満たしません。その上位互換性のあるGTMを用いましょう。
どのようなデータを可視化・見える化するか?
基本的に、上で述べたどの可視化手法でも、下のような図のデータセットが与えられたときに、可視化をすることができます。

ただ中には、サンプル間の類似度さえ与えられたら、可視化できるものもあります。下図のように、すべてのサンプル間で、それぞれのサンプルが類似している度合いが与えられている状況です。
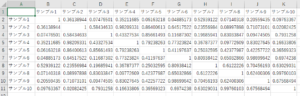
そのような手法の例としては、
- MDS
- Isomap
- Kernel PCA
- tSNE
があります。なお、MDS・Isomap・tSNEではサンプル間の距離が必要です。ユークリッド距離を用いたり、類似度を非類似度に変換して用いたりします。
サンプル間の類似度 (もしくは距離・非類似度) しか与えられていないときにはぜひご活用ください。
以上です。
質問・コメントがありましたら、twitter・facebook・メールなどを通して教えていただけるとうれしいです。