どの回帰分析手法でも変数重要度 (特徴量重要度) を計算する機能を DCEKit に搭載しました!重要度が 0 を有意に超えるようであれば、その説明変数 x はモデルの予測精度に貢献しているといえます。しかも、x の間に相関関係があっても、適切に重要度を計算できます。

変数重要度というと、ランダムフォレスト系の重要度が有名です。
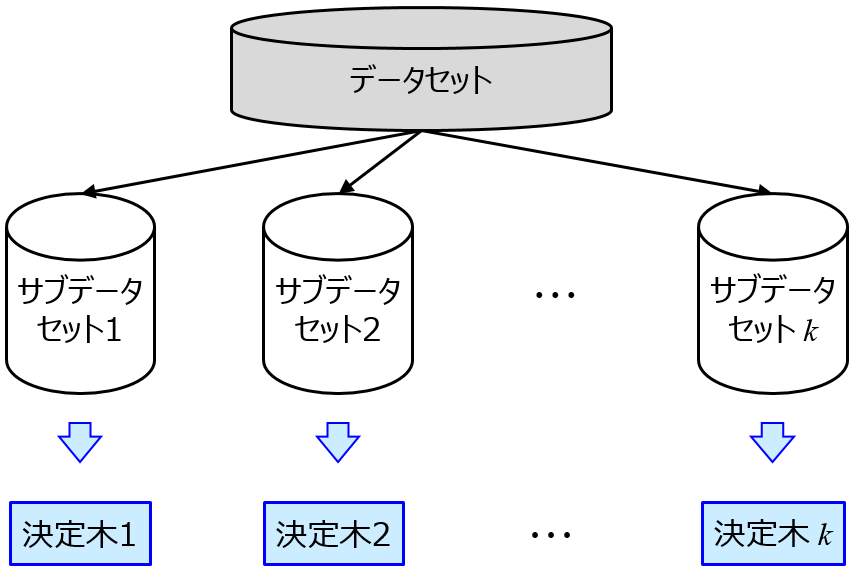
この x の重要度は、基本的にランダムフォレストのアルゴリズムに基づいているため、例えばサポートベクター回帰やガウス過程回帰などの、ランダムフォレスト以外の非線形回帰分析手法で回帰モデルの予測精度が良好だったときに、その手法でモデルを構築する上で x が重要かどうかを計算するわけではありませんでした。
こちらでも紹介したように、
金子研において、任意の回帰分析手法で変数重要度を計算する手法を開発しました。Cross-Validated Permutation Feature Importance (CVPFI) です。scikit-learn に搭載されている回帰分析手法であれば、どんな手法でもその手法でモデルを構築したときに重要度かどうかを示す指標を計算できます。
さらに、これまでの変数重要度は、ある変数 A と、A と相関の強い変数 B が x にあるとき、A や B が実際に重要であっても、変数重要度は低く見積もられてしまう問題がありましたが、CVPFI ではその問題を解決しています。A も B も (もし重要であれば) 変数重要度が高く計算されます。
CVPFI は DCEKit で計算できます。

DCEKit における以下のサンプルプログラムで、実際に CVPFI を使用しています。
- demo_cvpfi.py
- demo_cvpfi_gmr.py
これらを参考にしていただき、ご自身でおもちのデータセットにも CVPFI 展開していただければと思います。なお、回帰分析手法として GMR を用いる場合と、それ以外を用いる場合とで異なるためご注意ください。
回帰モデルの解釈をするときなどに、CVPFI を活用していただければと思います。なお CVPFI の重要度は、0 を有意に超えるようであれば、その x は少なくともモデルの予測精度に貢献しているといえますが、値がいくつ以上であれば重要というわけではありません。重要度の閾値について検討したいときは、乱数をうまく使うとよいでしょう。

また、CVPFI はランダムフォレストの変数重要度に代わるものであり、任意の回帰分析手法に対して用いることができますので、例えば Boruta の別の回帰分析手法バージョンを CVPFI に基づいて作成することも可能です。

ご参考になれば幸いです。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


