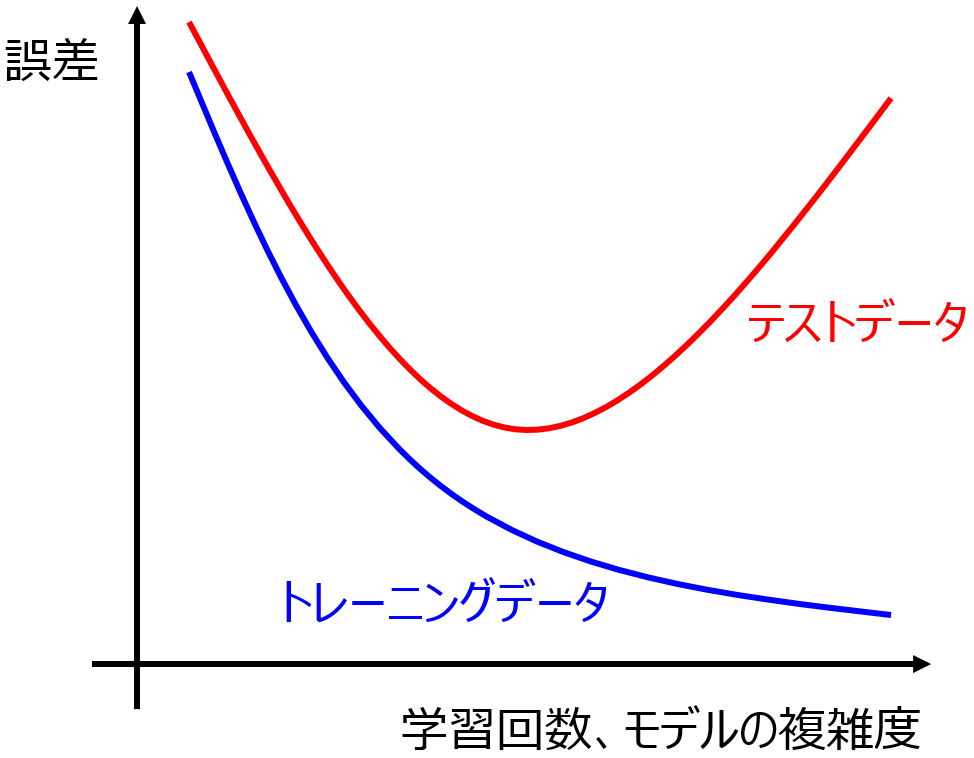
いつもどんな感じで回帰分析手法・クラス分類手法を選んでいるかお話します。予測結果の r², RMSE, MAE, 正解率, … といった指標だけ見て選んでいるわけではありません。

いろいろな回帰分析手法やクラス分類手法がありますね。

データ解析に関するいろいろな手法を解説した記事や、データ解析をするときの考え方の記事をまとめました。興味のある内容がございましたら、ぜひリンクへ飛んでいただけたらと思います。 pdfファイルやパワーポイント(pptx)ファイルは、自由にご利...

現状、どんなデータセットにも使えるベストな回帰分析手法、ベストなクラス分類手法が存在するわけではありません。なので、いま解析しているデータセットにあう手法を、選ぶ必要があります。

実際わたしも、多いときで 23 の手法の中から、データセットに合う手法を選ぶこともあります。基本的には、テストデータを予測した結果や、ダブルクロスバリデーションの結果を見て選びます。テストデータやダブルクロスバリデーションの詳細については以下をご覧ください。

回帰モデル・クラス分類モデルを評価・比較するためのモデルの検証 (Model validation)

いろいろな回帰モデル・クラス分類モデルを構築したり、モデルの中のハイパーパラメータ (PLSの成分数など) を決めたりするとき、モデルを評価・比較しなければなりません。そのためのモデルの検証 (model validation) の方法につ...

ダブルクロスバリデーション(モデルクロスバリデーション)でテストデータいらず～サンプルが少ないときのモデル検証～

回帰モデルやクラス分類モデルを検証するときの話です。モデルの検証一般的には、データセットが与えられたとき、サンプルをモデル構築用サンプル (トレーニングデータ, training dataset) とモデル検証用サンプル (テストデータ...

ただ、モデルの検証にあるような、回帰分析における r², RMSE, MAE だけ、クラス分類における正解率、精度、検出率だけ、チェックしているわけではありません。

回帰分析

回帰分析では、目的変数 y の実測値 vs. 推定値プロットも見ています。

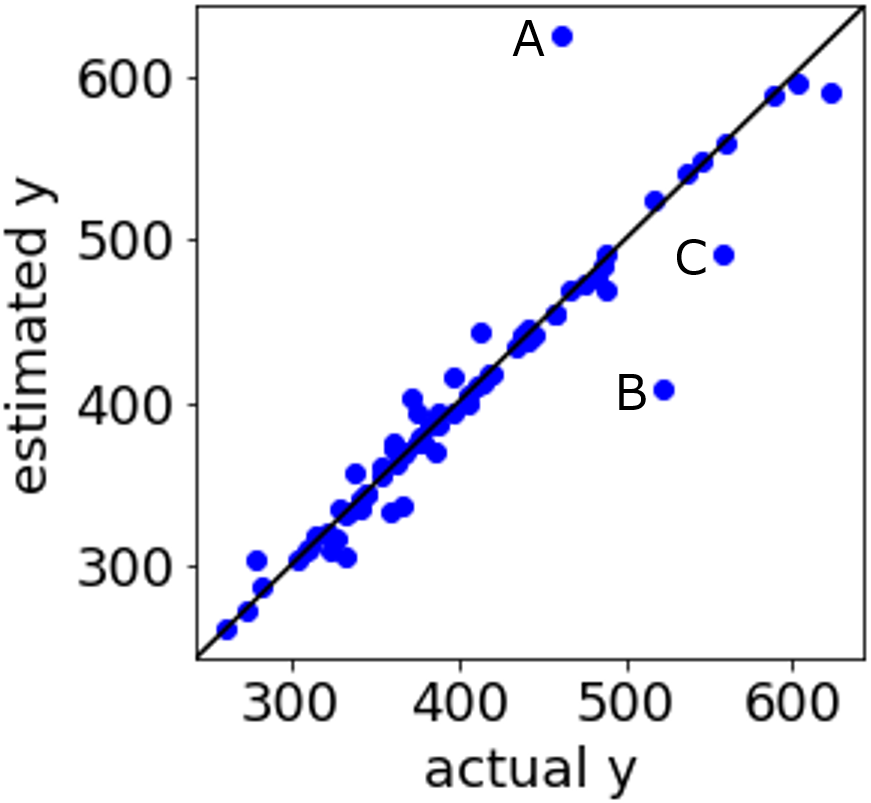
回帰分析における目的変数の実測値 vs. 推定値プロットを、解像度を上げて見る

解像度を上げるといっても、画素の密度を上げるわけではなく、より詳細に検討するということです。回帰分析をしたら、以下のような目的変数の実測値 vs. 推定値プロットが得られたとしましょう。ちなみにこのプロットは、こちらの論文にある沸点のデ...

というのも、回帰分析をするということは、構築された回帰モデルを用いる目的があります。たとえば、分子設計や材料設計において、y が小さい値の分子構造・材料を設計したいとか、y が大きい値の分子構造・材料を設計したいとかです。y の値を評価するために、ある範囲の y の値を予測したいときもあるでしょう。

y の実測値 vs. 推定値プロットを見て、y の値を予測したい付近の予測誤差はどうなっているか、チェックします。r² の値は少し小さくても、RMSE, MAE の値は少し大きくても、目標の y の値に近いところの予測誤差が小さくなっている回帰分析手法があるかもしれません。そういった回帰分析手法を選ぶこともあります。

r², RMSE, MAE だけからはわからない手法の特徴を確認するため、y の実測値 vs. 推定値プロットをチェックするわけですね。

クラス分類

クラス分類における予測結果として、正解率、精度、検出率だけでなく、混同行列 (confusion matrix) を必ず見ます。

回帰モデル・クラス分類モデルを評価・比較するためのモデルの検証 (Model validation)

というのも、クラス分類において、誤分類された結果にもいろいろな種類があるためです。たとえば二クラス分類において、False Negative (FN) と False Positive (FP) があります (FN, FP については上のリンクのページをご覧ください)。FN を小さくしたいのか、FP を小さくしたいのか、どのくらいのバランスで両方を小さくしたいのかは、クラス分類モデルを用いる目的によって変わります。

なので、混同行列をチェックして FN, FP を確認します。正解率は少し小さくても、FN が小さいクラス分類手法や、FP が小さいクラス分類手法があるかもしれません。そういったクラス分類手法を選ぶこともあります。

正解率だけからはわからない手法の特徴を確認するため、混同行列をチェックするわけですね。

説明変数 x の重要度も知りたい！

回帰分析でもクラス分類でも、説明変数 x の重要度を確認したいときがあります。モデルを用いるだけでなく、そのモデルにおける x の重要度を知ることも目的に入っているときは、あらかじめ手法を選んでおく必要があります。わたしの場合は、決定木 (Decision Tree, DT), ランダムフォレスト (Random Forests, RF), Gradient Boosting Decision Tree (GBDT), XGBoost, LightGBM といった決定木系を用います。

決定木(Decision Tree, TD)～直感的に分かりやすいモデル～

決定木(Decision Tree, TD)について、pdfとパワーポイントの資料を作成しました。データセットが与えられたときに、決定木で何ができるか、決定木をどのように計算するかが説明されています。pdfもスライドも自由にご利用ください。...

ランダムフォレスト(Random Forests, RF)～アンサンブル学習で決定木の推定性能を向上！～

ランダムフォレスト(Random Forest, RF)について、pdfとパワーポイントの資料を作成しました。データセットが与えられたときに、RFで何ができるか、RFをどのように計算するかが説明されています。pdfもスライドも自由にご利用く...

[デモのプログラムあり] 勾配ブースティングGradient Boosting、特に Gradient Boosting Decision Tree (GBDT), XGBoost, LightGBM

勾配ブースティングGradient Boosting、特に Gradient Boosting Decision Tree (GBDT), XGBoost, LightGBM について、パワーポイントの資料とその pdf ファイルを作成しま...

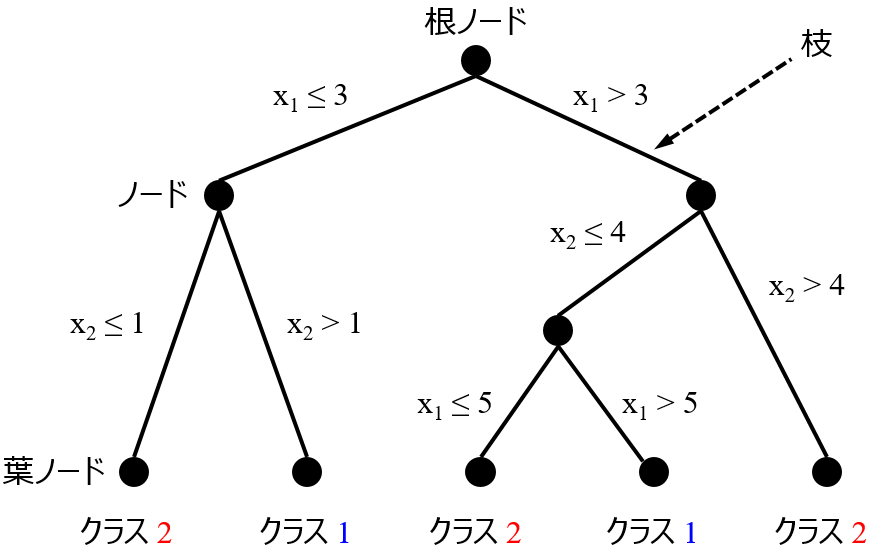
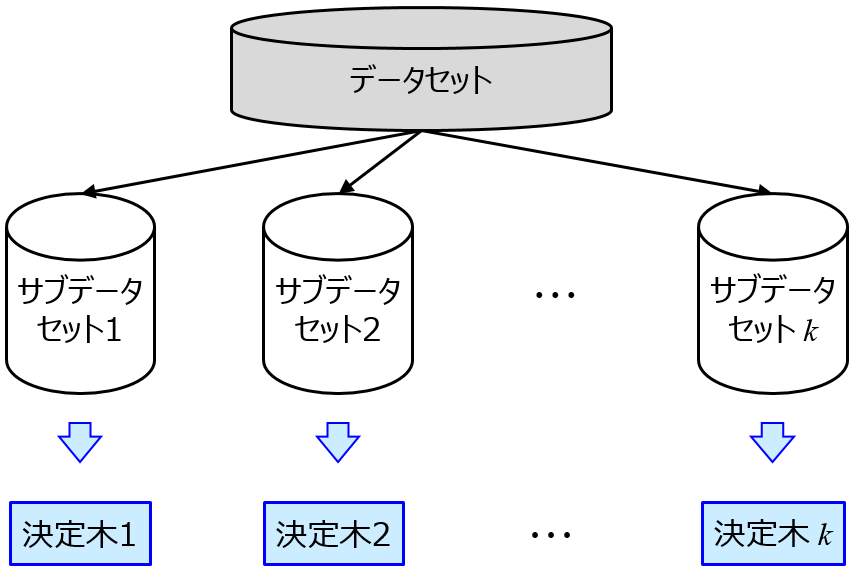
ちなみに、こちらの論文でも用いられている、

シトクロムP450の阻害剤・非阻害剤をクラス分類する論文。Pubchem BioAssay Databaseを使用。記述子として3種のfingerprints, MOE, PaDELを検討。回帰手法としてRF, GBDT, XGBoost, DNN, CNNを検討。SHAPで記述子の重要度を計算してモデルを解釈し、誤分類された分子を分析https://t.co/Mbcco0BeZd

— 金子弘昌＠発売中「化学のための Pythonによるデータ解析・機械学習入門」 (@hirokaneko226) November 29, 2019

SHAP (SHapley Additive exPlanations) を用いれば、各 x の値の、y の予測値に対する影響を、正か負かも含めて、計算できます。ただ、SHAP ではあるサンプル周りを線形近似していますので、データセット全体における y に対する各 x の寄与を求めるのではなく、興味のあるサンプル周りにおける、ローカルな y に対する各 x の寄与を検討するのがよいと思います。