回帰モデルやクラス分類モデルを構築したら、モデルの逆解析をすることがあります。逆解析では、説明変数 (記述子・特徴量・実験条件など) X の値から目的変数 (物性・活性など) y の値を推定するのではなく、逆に、y の値から X の値を推定します。化学構造設計・分子設計・材料設計などに応用されます。Invers QSPR や Inverse QSAR と呼ばれたりもします。モデルの逆解析についての詳細はこちらをご覧ください。

モデルの逆解析をしたい状況はたくさんあります。それらを大きく分けると、以下の3つになります。
- y の値をなるべく大きく (または小さく) する、もしくは y を既存の値より大きく (または小さく) することである範囲内に入るような、X の値を得たい
- y が既存のクラスもしくは既存の値と同じ値くらいに、いろいろな X の値を発生させたい
- y の種類が複数あり、それぞれの y の値は既存の値くらいであるが、それらの組み合わせ的に新規な結果になる X の値を獲得したい
1. は分かりやすいと思います。物性や活性などを向上させたいケースです。2. は、たとえば特許などである化学構造は押さえられているため、y の値は同じくらいで OK ですが、その化学構造とは似ていない新規構造が欲しい、といった場合です。3. は複数の y がトレードオフの関係にあり、パレート最適解を更新したい、といった状況です。
ここで注意しないといけないのは、1. のケースで、回帰分析手法として決定木 (Decision Tree, DT) やランダムフォレスト (Random Forest, RF) を使うときです。決定木やランダムフォレストは 1. のケースが苦手、というか、y の値を既存の値より大きくしたり小さくしたりするのが原理的に不可能なのです。
決定木を回帰分析に用いるときは、次の図のようになります。
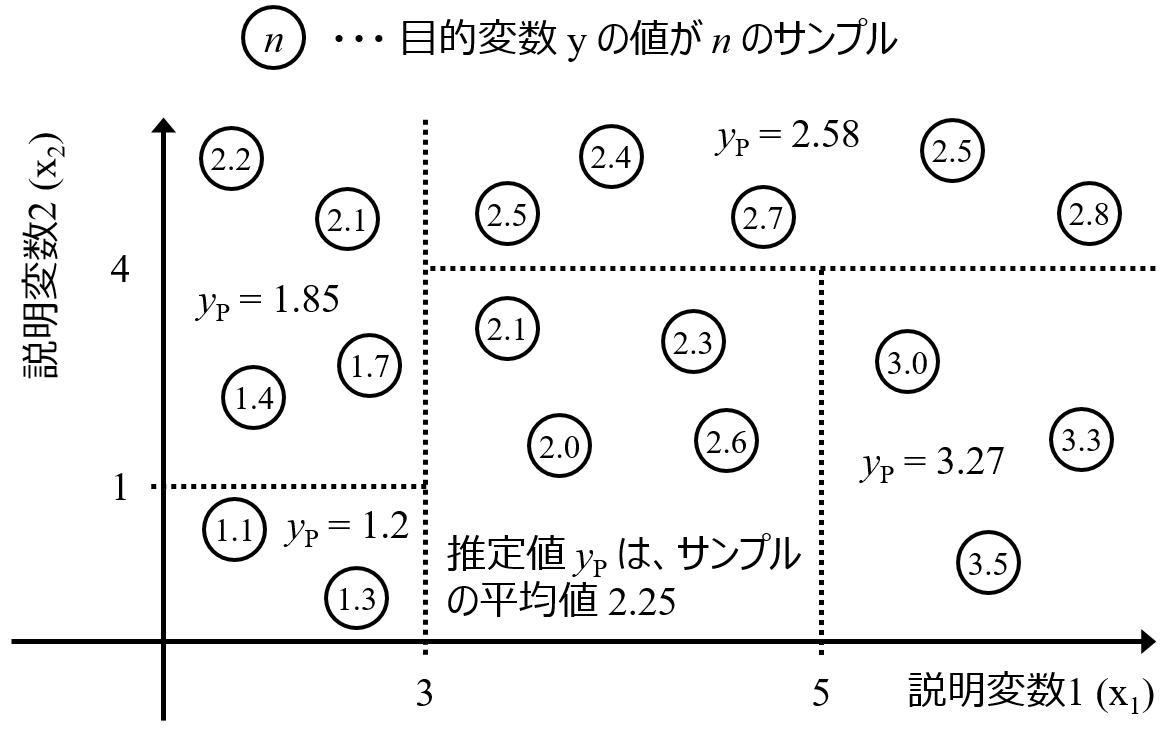
新しいサンプルの y の値を推定値は、(いくつかの) トレーニングサンプルの y の値の平均値で与えられます。つまり、y の推定値が、トレーニングデータの y の最大値を上回ったり、y の最小値を下回ったりすることはありえない、ということです。ランダムフォレストは、決定木をたくさん作ったものです。y の推定値は決定木の推定値を平均したものなので、y の推定値の上限下限について、決定木と同じことがいえます。
決定木やランダムフォレストの詳細についてはこちらをご覧ください。
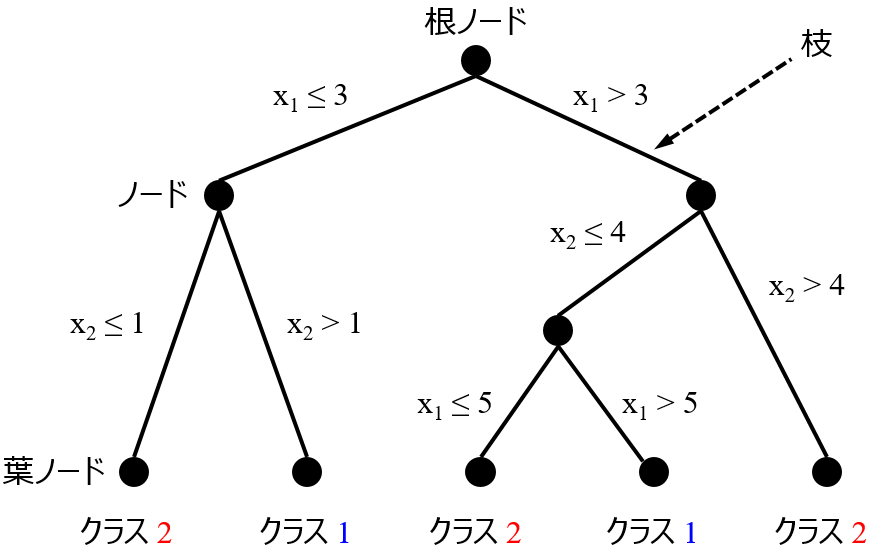
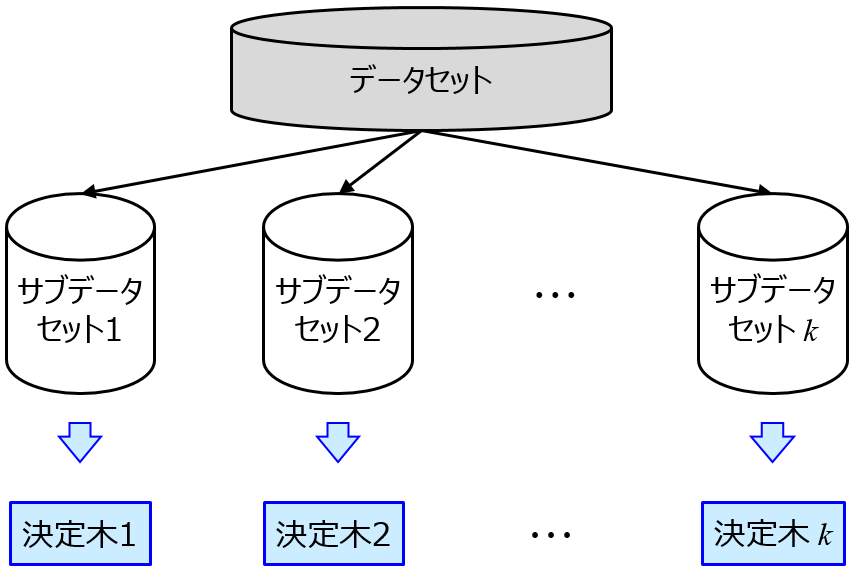
このように、決定木やランダムフォレストは逆解析において、トレーニングデータの y の最大値や最小値を更新するような、X の値を得ることはできません。決定木やランダムフォレストで構築されたモデルを逆解析に用いるときは注意しましょう!
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。

