よくある誤解の一つに、線形モデルは予測精度が低いけど外挿性が高い、非線形モデルは予測精度が高いけど外挿性が低い、というのがあります。回帰モデルが線形だからといって非線形モデルより予測精度が低いわけではありませんし、線形モデルだからといって非線形モデルより外挿性が高いわけでもありません。線形モデルが、説明変数 x のより広範囲を精度よく予測できるわけではないのです。
モデルの予測精度は、線形・非線形に限らず、データセット、すなわちサンプル・目的変数 y・説明変数 x の組み合わせに依存します。また、線形モデル、非線形モデルといっても、モデル構築手法にはそれぞれ様々な種類があります。線形、非線形の二種類だけで、予測精度を議論できる単純なものでもありません。
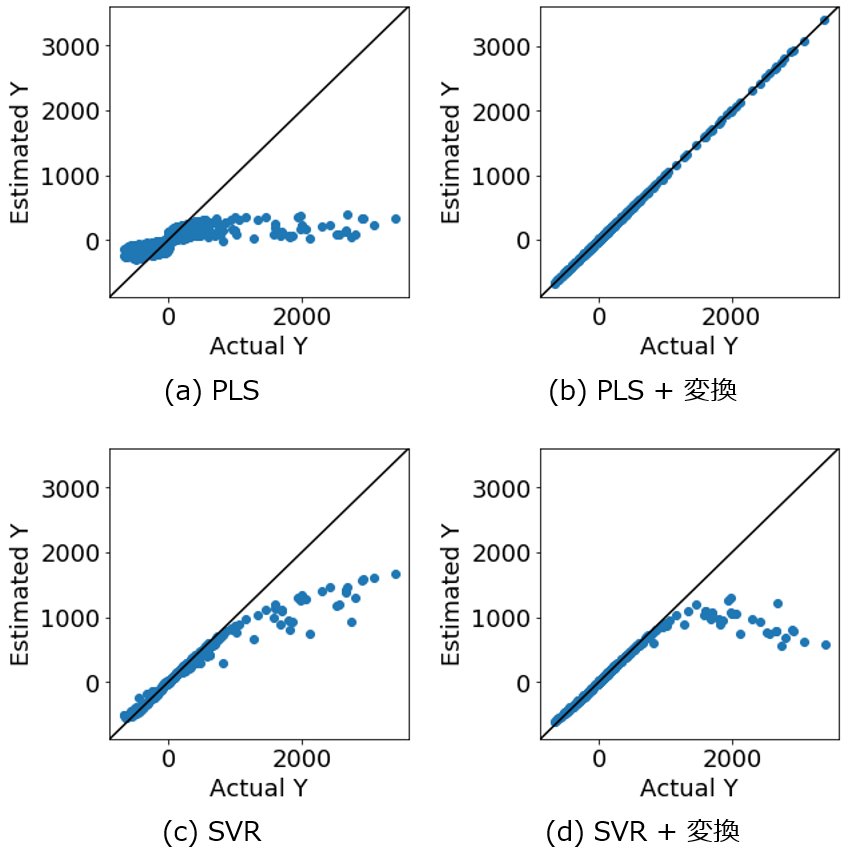
仮に、あるデータセットにおいて、ある線形回帰モデル、例えば PLS の予測精度が高かったとします。これはあくまで、データセットのサンプルの x の範囲内では、線形モデルで近似できたということであって、その範囲外も線形関係が成り立つとは、まったくいえません。サンプルが追加されたら、y と x の間の関係に線形性が出てくる可能性があります。
非線形回帰モデル、例えばガウシアンカーネルを用いた SVR が最も良かったのであれば、もちろん SVR を用いて最終的に用いるモデルを構築した方がよいですし、外挿領域の予測をしたいときにも、SVR モデルを使用するべきです。
構築したモデルの予測精度は、今あるデータセットの y が測定されたサンプルでしか検証できないことから、結局は 「内部」 バリデーションに過ぎません。線形モデルとはいえ、(テストデータ含めて) 今あるデータセットより外挿を予測できる保証はありません。トレーニングデータとテストデータに分けて、トレーニングデータで構築されたモデルをテストデータで検証すること自体はまったく問題ないのですが、テストデータも結局は既にあるデータであり、内部データです。テストデータを精度よく予測できるからといって、いくらでも外挿できるわけではありません。
どうしても外挿を探索したい場合は、物理モデル・第一原理モデルを使用したり、組み合わせたりするとよいです。
物理モデルや第一原理モデルの理論が成り立つ領域では、外挿することができます。
データ解析・機械学習でモデル構築したい場合には、適切にモデルの適用範囲を決めて、外挿の中でも予測できると考えられる領域までを予測するようにします。

それより外側の外挿領域を探索したいときには、ベイズ最適化をはじめとする適応的実験計画法・能動学習と組み合わせて、データ解析・機械学習と実験を合わせて探索するようにしましょう。

以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


