金子研の論文が Analytical Science Advances に掲載されましたので、ご紹介します。タイトルは
です。
潜在変数モデルであり、ガウス過程による教師なし学習である Gaussian Process Latent Variable Model (GPLVM) を用いて、プラントで測定されているようなプロセスデータの可視化やプロセス状態の推定を実施しました。
ガウス過程というと、ベイズ最適化にも用いられるガウス過程回帰が有名かもしれません。

ガウス過程回帰は教師あり学習法であり、目的変数 Y があるときに用いる一方で、Y がないときに用いる教師なし学習法としてのガウス過程の手法もあります。こちらで解説している GPLVM です。

今回はこの手法を、時系列データを可視化したり、プラントにおけるプロセス状態を推定したりすることに応用しました。GPLVM には、モデルのパラメータの推定方法や潜在変数の事前分布の違いによって、いろいろな手法があります。この論文ではそれらの中で以下の三つの手法に着目しました。
- Bayesian Gaussian Process Latent Variable Model (BGPLVM)
- infinite Warped Mixture Model (iWMM)
- Gaussian Process Dynamical Models (GPDM)
BGPLVM では潜在変数の事後分布やハイパーパラメータを変分ベイズ法で推定します。 BGPLVM では潜在変数の事前分布は一つの正規分布ですが、iWMM では潜在変数の事前分布が混合正規分布で表されます。また GPDM では潜在変数の事前分布に時系列データの特徴が考慮され、具体的にはマルコフ過程を仮定して設定されます。ちなみに GPDM はこちらの論文でも用いられています。

これらの手法や、プロセスの動特性を考慮するために時間遅れ変数を考慮した手法 (GPDM では潜在変数の事前分布でも考慮されていますが、比較のために時間遅れ変数を追加しました) を用いて、お馴染みの Tennessee Eastman プロセスのデータセットで比較しました。プロセス状態の数を 4 つ、6 つ、8 つ、10 つと増やしながらデータの可視化をしていったところ、それぞれ良好に可視化できることが確認されました。また、可視化した二次元平面上において、プロセス状態ごとにサンプルが適切に固まっているか確認するため、ランダムフォレストにより
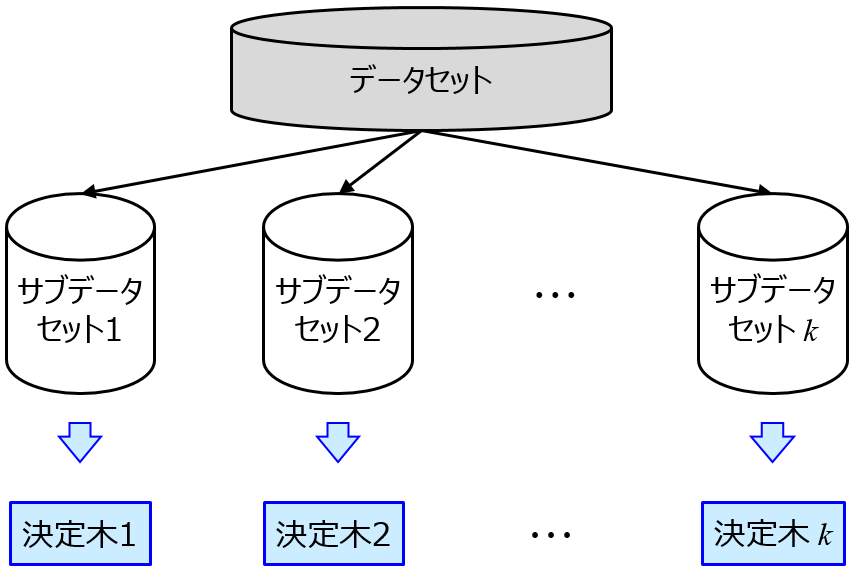
プロセス状態の推定としてクラス分類をしたところ、BGPLVM, iWMM, GPDM の順に分類精度が高いことがわかりました。特にGVDM では、プロセス状態の数が 4 個のときは 100 %、プロセス状態の数が 10 個のときでも 90% の正解率を達成しています。
プロセスの可視化やプロセス状態に推定に関して、ガウス過程による潜在変数モデルが有効と考えています。ご興味がございましたらお読みいただけますと幸いです。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


