どうしてクロスバリデーションしないの？

データ解析をしていると、いろいろな理由でクロスバリデーションを使いたくない、もしくはクロスバリデーションを使えないことがあります。

一つはサンプルが少なすぎるときです。クロスバリデーションでは、最初のトレーニングデータから、さらにトレーニングデータとバリデーションを分けます。トレーニングデータにより構築した回帰モデルを用いてバリデーションデータを推定することを繰り返すわけです。そのため、クロスバリデーション内でモデルを構築するときには、最初のトレーニングデータのサンプル数からさらにサンプル数が小さくなってしまいます。たとえば、トレーニングデータのサンプル数が10のときなど、元々サンプル数が小さいときには、さらにトレーニングデータのサンプルが少なくなったクロスバリデーション内において安定的な回帰モデルが構築されるとはいえません。

また二つ目として、サンプル数が多すぎるときもクロスバリデーションを使いたくないのです。たとえば、5-fold クロスバリデーションでは、トレーニングデータによる回帰モデル構築とバリデーションデータの予測を5回も繰り返さなければなりません。サンプル数が多いと、特に回帰モデルの構築に時間がかかるため、モデル構築の回数はなるべく減らしたいのです。

最後に、すでに構築されている回帰モデルの推定性能を評価したいときです。クロスバリデーションは、トレーニングデータとバリデーションデータを変えてモデル構築と予測を繰り返すため、すでに構築されたモデルの推定性能を評価することができません。

クロスバリデーション以外で、どうやって回帰モデルの性能を評価する？

クロスバリデーションせずに、新しいデータに対する非線形回帰モデルの予測性能を評価する方法があります。それは、トレーニングデータにおけるサンプルの中点を使った方法です。

中点はとても単純で、たとえば 1 と 5 の中点は (1+5)/2 = 3 になります。

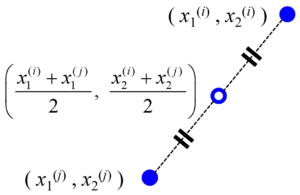
同じように２つのサンプルにおいて、説明変数X・目的変数yそれぞれで中点を計算し、それをあたかも実際のサンプルのように扱います。中点サンプルを集めたものを、バリデーションデータとして用いるわけです。

ただ、中点を計算するといっても、トレーニングデータにおけるすべてのサンプルの組み合わせで中点を計算するわけではありません。というのも、バリデーションデータとしては、トレーニングデータと同じデータ分布に従うようなサンプルが欲しいわけですが、たとえば変数間に非線形性があるとき、遠く離れた２点の中点は、データ分布から離れた点になってしまう可能性もあります。

そのため、あるサンプルについて、そのサンプルと最も距離が近い k 個のサンプルとの間だけ、中点を計算します。k最近傍法みたいですね。なので、この中点を、midpoints between k-nearest-neighbor data points of a training dataset (midknn) と呼びます。この midknn を、あたかも実際のサンプルのように、バリデーションデータとして使用して、推定性能が高くなるように非線形回帰モデルのハイパーパラメータを選択します。クロスバリデーションのかわりに、midknn によるバリデーションをするのです。たとえば、midknn の決定係数 r² である r²_midknn が最大になるハイパーパラメータを選択したり、midknn の Root-Mean-Squared Error (RMSE) である RMSE_midknn が最小になるようにハイパーパラメータを選択したりします。

ちなみに k としては 10 がオススメです。

こちらのGitHubに midknn を計算するためのインデックス、つまりトレーニングデータの何番目と何番目で中点を計算すればよいか、を出力する関数がありますので、ぜひご活用ください。さらに、非線形回帰分析手法の一つであるサポートベクター回帰 (Support Vector Regression, SVR)

サポートベクター回帰(Support Vector Regression, SVR)～サンプル数10000以下ならこれを使うべし！～

サポートベクター回帰(Support Vector Regression, SVR)について、pdfとパワーポイントの資料を作成しました。データセットが与えられたときに、SVRで何ができるか、SVRの特徴、どのように計算するかが説明されてい...

を例にして、midknn によりハイパーパラメータを最適化するデモを実行できるプログラムもあります。ぜひご利用ください。

GitHub - hkaneko1985/midknn: Midpoints between k-nearest-neighbor data points of a training dataset (midknn) as a validation dataset in regression

Midpoints between k-nearest-neighbor data points of a training dataset (midknn) as a validation dataset in regression - ...

midknnであれば、上にあげたクロスバリデーションの問題点を解決できます。

midknnによりバリデーションデータを新たに作成するため、トレーニングデータのサンプルをすべてモデル構築用として利用できます。また回帰モデルの推定性能を評価するとき、つまり r²_midknn や RMSE_midknn を計算するとき、一度だけモデルを構築して midknn のデータを推定すればよいため、クロスバリデーションのように何回もモデル構築と予測を繰り返さなくても OK です。そして、すでに構築されたモデルがあるときも、midknn の X の値をそのモデルに入力して y の値を推定し、midknn の y の値と比較して r²_midknn や RMSE_midknn を計算することでモデルの評価ができます。あらかじめ構築されたモデルの推定性能でも評価できるわけです。