分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築し、構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。
モデルの予測精度を評価する時に、データセットをトレーニングデータとテストデータに分割し、トレーニングデータで構築されたモデルを用いてテストデータを予測し、その予測誤差を確認します。データセットのサンプル数が小さい時には、単純にトレーニングデータとテストデータに分割すると、それぞれのサンプル数がさらに少なくなってしまうため、ダブルクロスバリデーションを用いて、全てのサンプルをテストデータとして扱い、モデルの予測精度を評価します。


ダブルクロスバリデーションにおいて外側の分割数をサンプル数とする、すなわち leave-one-out にすることで、トレーニングデータのサンプル数も (全サンプル数 − 1) にできます。ダブルクロスバリデーションにより、トレーニングデータのサンプル数もテストデータのサンプル数も最大化して、モデルの予測精度を評価できます。
ただし、ダブルクロスバリデーションを実施するとしても、少なくとも1つのサンプルはテストデータにしなければなりません。例えば1つのサンプルだけ y の値が他のサンプルと比較して大きいと、y の値の小さいサンプルで構築されたモデルを用いて y の値が大きいサンプルを予測する必要があります。もちろん、y の値の少ないサンプルで適切に x と y の関係をモデル化できれば、y の値が大きいサンプルも適切に予測できます。
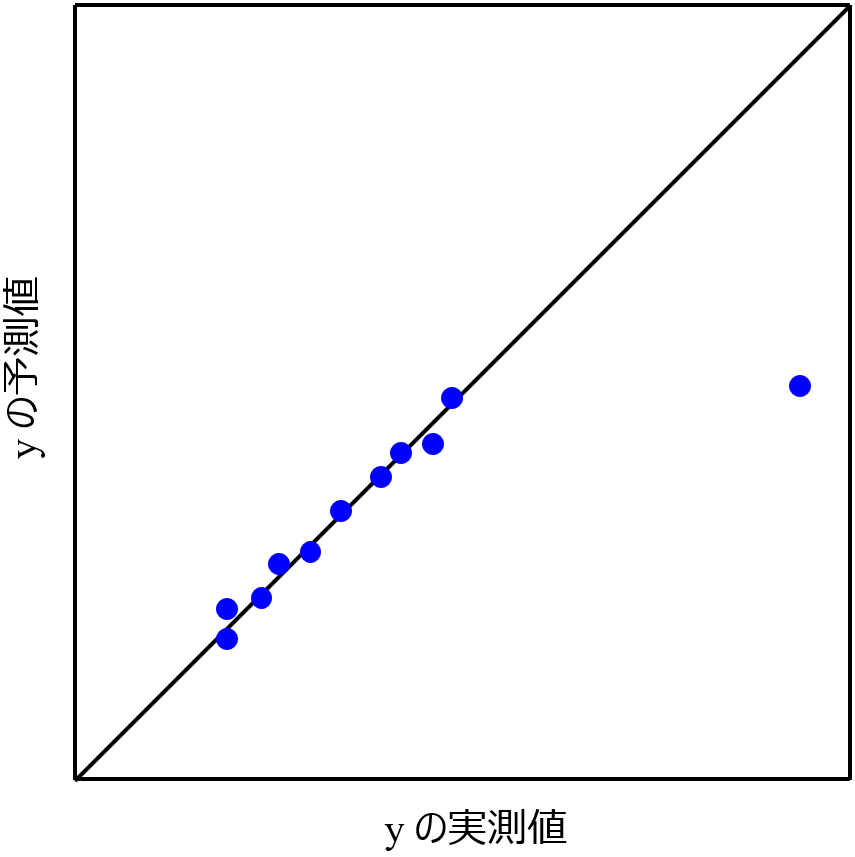
ただ多くの場合で、y の実測値とダブルクロスバリデーション後の y の予測値との間の関係を図示すると、以下のようになります。
y の値の小さいサンプルで構築されたモデルでは y の値が大きいサンプルを予測できず、そのサンプルだけ外れる、すなわち y の予測誤差が大きくなります。もちろん、ここで 「y の値が他のサンプルと比較して大きいから外れた」 とだけ結論付けるのではなく、サンプルを調べて外れた要因を検討します。
人によっては、上のような y の実測値と予測値の散布図を見た時に、外れている1つのサンプルを省いてモデル構築をしたら良いのではないかとか、他の回帰分析手法を検討しほうが良いのではないかとか考えると思います。
一方で、例えば重要な x の中に y の値が大きい1つのサンプルだけ値が0以外で他のサンプルは値が0のような x があれば、外れている要因はその x にあり、もしその x を用いて全サンプルで (全サンプルをトレーニングデータにして) モデル化すれば、ダブルクロスバリデーションによる評価において y の実測値と予測値の散布図の対角線から外れたサンプルを含めて、問題なくモデル化できると考えられます。さらに言えば、そのようにして構築されたモデルを用いることで、対象となる x の値をさらに変化させることで、y の値を (外れたサンプルよりも) さらに向上させられると期待もできます。
以上のように、特にサンプル数が小さい場合は、ダブルクロスバリデーションによりモデルの予測精度を評価する時に、r2 などの評価値を見るだけでなく、y の実測値と予測値の散布図を必ず確認し、例えば上のようになった時には外れサンプルとなった要因を調査しましょう。そして外れサンプルとなった要因を的確に説明できる時には、全サンプルを用いてモデルを構築し、他のサンプルを予測したりモデルの逆解析をしたりして問題ありません。むしろ、このモデルを用いることで、興味深い予測結果や逆解析結果が得られるかもしれません。
以上です。
質問やコメントなどありましたら、X, facebook, メールなどでご連絡いただけるとうれしいです。