モデルの検証と、その後についての話です。

データセットをトレーニングデータとテストデータに分け、テストデータを用いて、トレーニングデータで構築されたモデルの検証をします。検証の中で、テストデータを精度良く推定できる手法 (回帰分析手法・クラス分類手法) を選択します。その後は、すべてのデータセットでモデルを構築し、モデルの適用範囲 (Applicability Domain, AD) を設定してからモデルを運用します。AD についてはこちらをご覧ください。

テストデータでモデルの検証をするとき、テストデータのすべてのサンプルを誤差 0 で推定できるモデルが理想的です。すべての誤差を 0 にすることは難しいかもしれませんが、データセットをトレーニングデータとテストデータに分けるとき、基本的にはランダムに分割したり、Kennard-Stoneアルゴリズムを用いたりしますので、トレーニングデータとテストデータとは同じデータ分布、もしくはトレーニングデータのデータ分布にテストデータのデータ分布が含まれることが期待でき、トレーニングデータに上手くフィットして、かつオーバーフィッティング
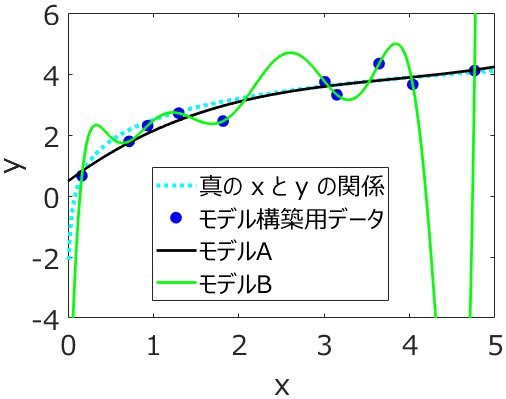
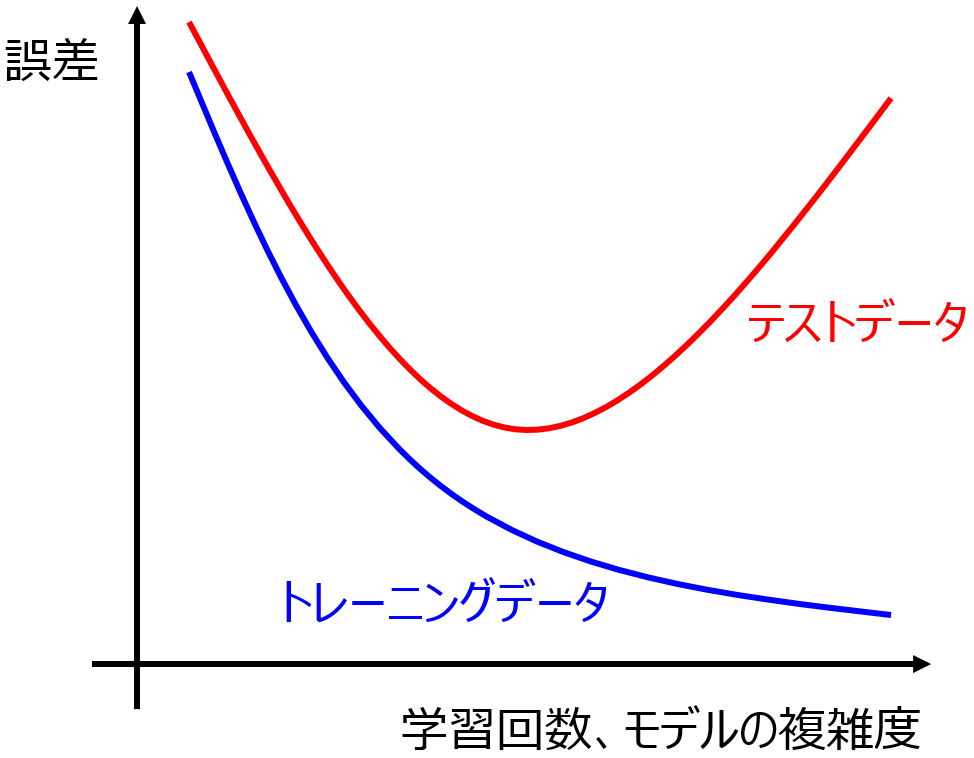
していなければ、トレーニングデータにおける推定誤差と同程度にまで小さくすることはできると考えられます。また、そのような分布のため、テストデータにおける推定性能を検証するときには、AD を設定することはあまりありません。
ただ、データセットに外れ値・外れサンプルがあったり、
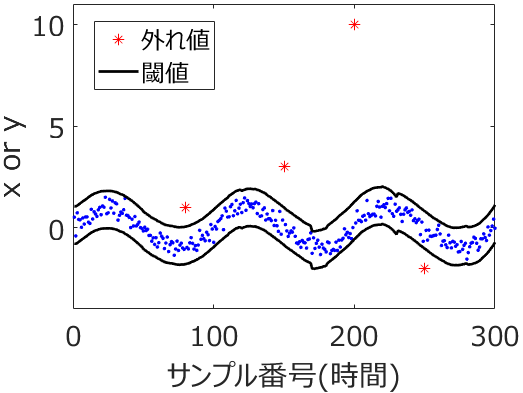
説明変数 x と目的変数 y の分布が複雑であったり、x と y の非線形関係が強かったり、サンプル数が小さかったりして、トレーニングデータのデータ分布とテストデータのデータ分布が同じとは仮定できないときもあります。そんなとき、たとえば回帰分析において、テストデータの推定結果における実測値 vs. 推定値プロットに、対角線から大きく外れたサンプルが出てくることがあります。そして、いろいろな回帰分析手法によって構築されたモデルの推定性能を比べるときに、テストデータ全体で誤差が小さいわけではなく、その外れたサンプルをたまたま誤差小さく予測できたようなモデルが、決定係数 r2 が大きくなったり、誤差の平均値のような指標である RMSE や MAE が小さくなったりして、選ばれる可能性があります。その外れたサンプル付近を精度良く推定したいときは、それでよいかもしれませんが、全体的に上手く推定したときには、そのような状況は望ましくありません。
外れたサンプルは AD の外であることが考えられますので (そうでないこともあります)、そんなときには、テストデータにおける推定性能を検証するときにも、AD を設定するとよいでしょう。AD 内のサンプルのみで、推定性能を検証するわけです。
テストデータでの検証を終えて、回帰分析手法が決まり、すべてのデータセットでモデル構築するとき、外れサンプルがあり、検討した結果、外れサンプルを削除することになったとしましょう。ちなみに、削除ではなく補完したい場合はこちらをご覧ください。

外れサンプルを削除して、最終的なモデルを構築することになったとき、もちろん外れサンプルの理由にもよりますが、AD を考慮するときに用いたほうがよいでしょう。具体的には、削除した外れサンプルと近いサンプルも外れサンプルの可能性がありますので、y の値を推定する新しいサンプルが、削除した外れサンプルと近い距離にあるとき、AD 外とすることも検討するのがよいと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


