ベイズ最適化において、複数の実験候補を選択するお話です。ベイズ最適化についてはこちらをご覧ください。
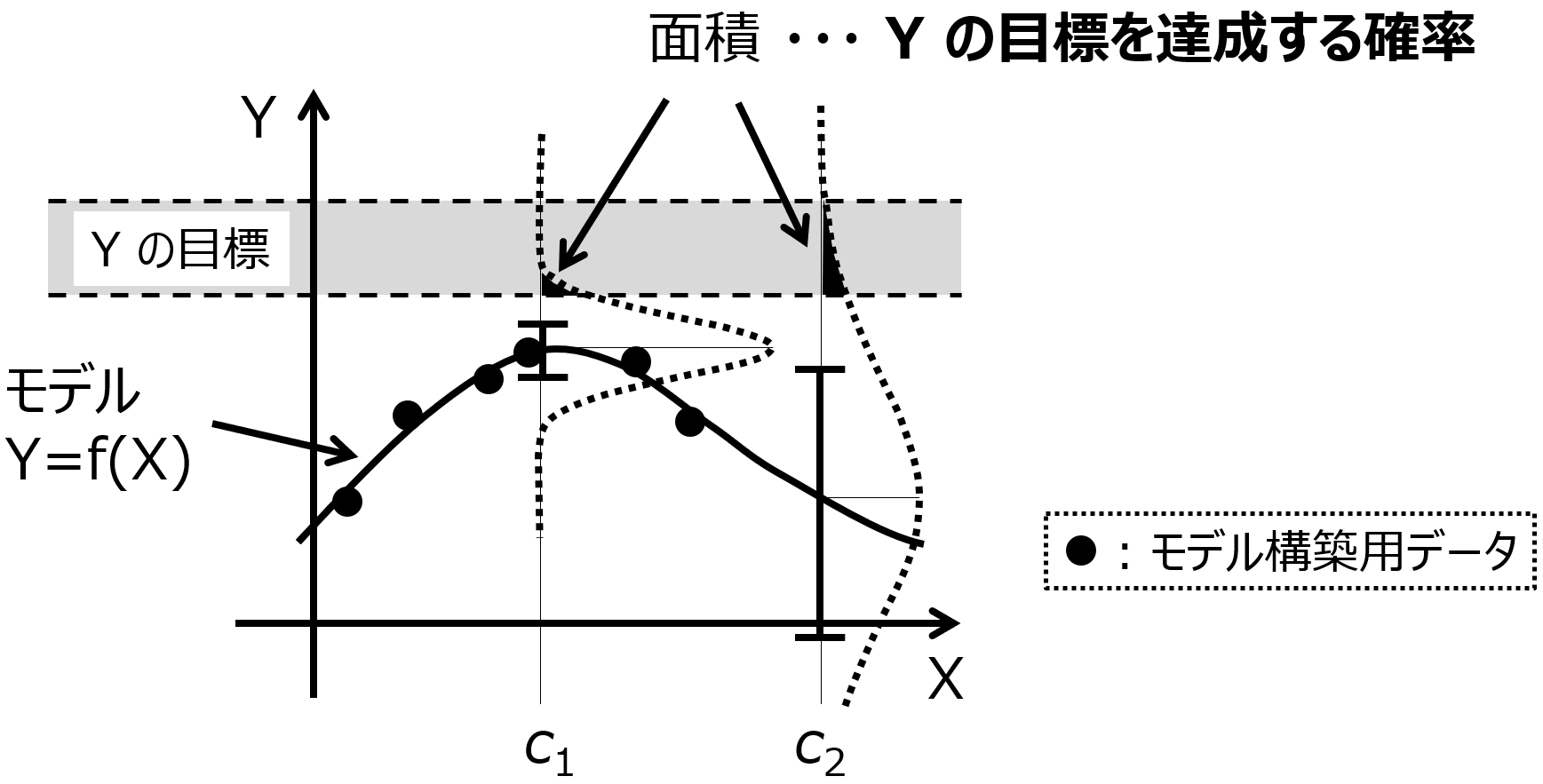
ベイズ最適化では、以下の 1. – 4. を繰り返すことで、物性や活性などの目的変数 Y が向上したり目標値を達成したりできる、実験条件などの説明変数 X を探索します。
- データセットを用いてガウス過程回帰によりモデル Y=f(X) を構築する
- 獲得関数の値が大きい X の値の候補を選択する
- 2. で選択された候補で実際に実験して、Y の値を得る
- X と Y の値をデータセットに追加する
選択する際の多数の候補群は、たとえばこちらの方法で生成できます。
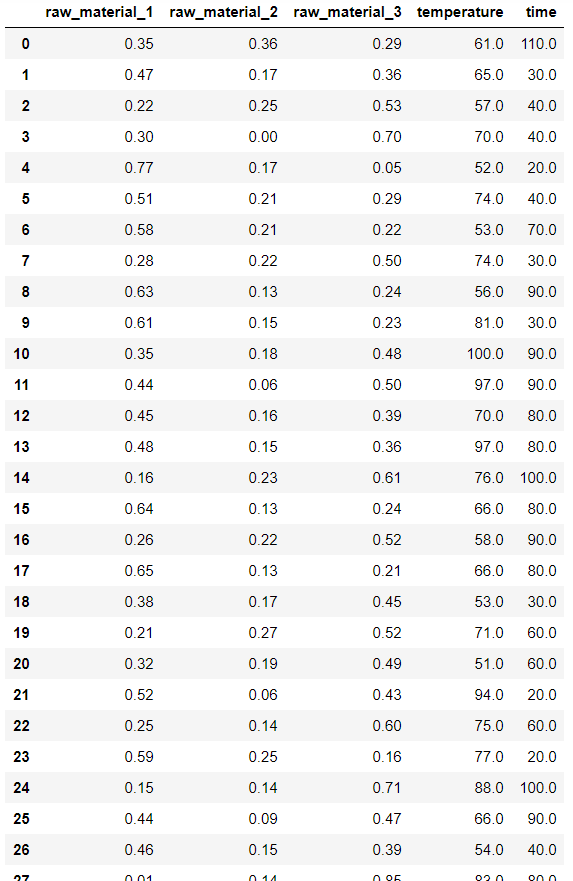
ちなみにベイズ最適化は Y が複数あっても OK です。

上の 3. の実験において、一度に複数回の実験ができれば、4. において複数のサンプルをデータセットに追加できます。そこで、2. において、複数の X の値の候補を選択することを考えます。
すぐに思いつくのは、獲得関数の値の大きい順に X の値の候補を並び替え、上から (大きい順に) 複数個、選択する方法です。ただ、X の値が似ていると、獲得関数の値も似たものになり、その逆 (獲得関数の値が似ていると、X の値も似ている) は必ずしもいえませんが、獲得関数の値が似ていると、X の値も似ている可能性はあります。複数個選択したとき、どれも似たような実験候補になってしまうことがあるのですね。同じような実験では、実験結果 (Y の値) も似たようになる可能性が高く、面白みがありません。有望そうな実験候補の中で、似ていないものを選びたいですね。
複数の候補を選択する手法はいろいろありますが、その中でもシンプルな方法を紹介します。
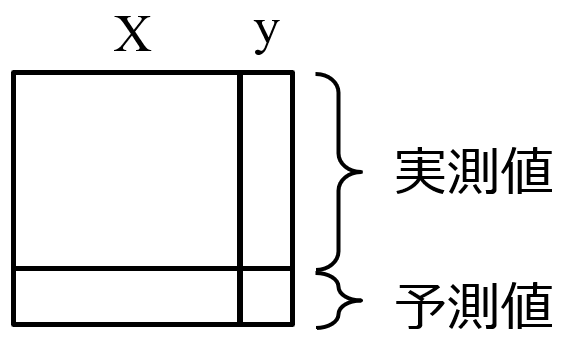
Y の予測値を用いてデータベースにサンプルを追加して、2, 3, 4, … 個目の候補を選択するとよいです。

類似した候補が選ばれにくくなります。具体的な手順は以下のとおりです。
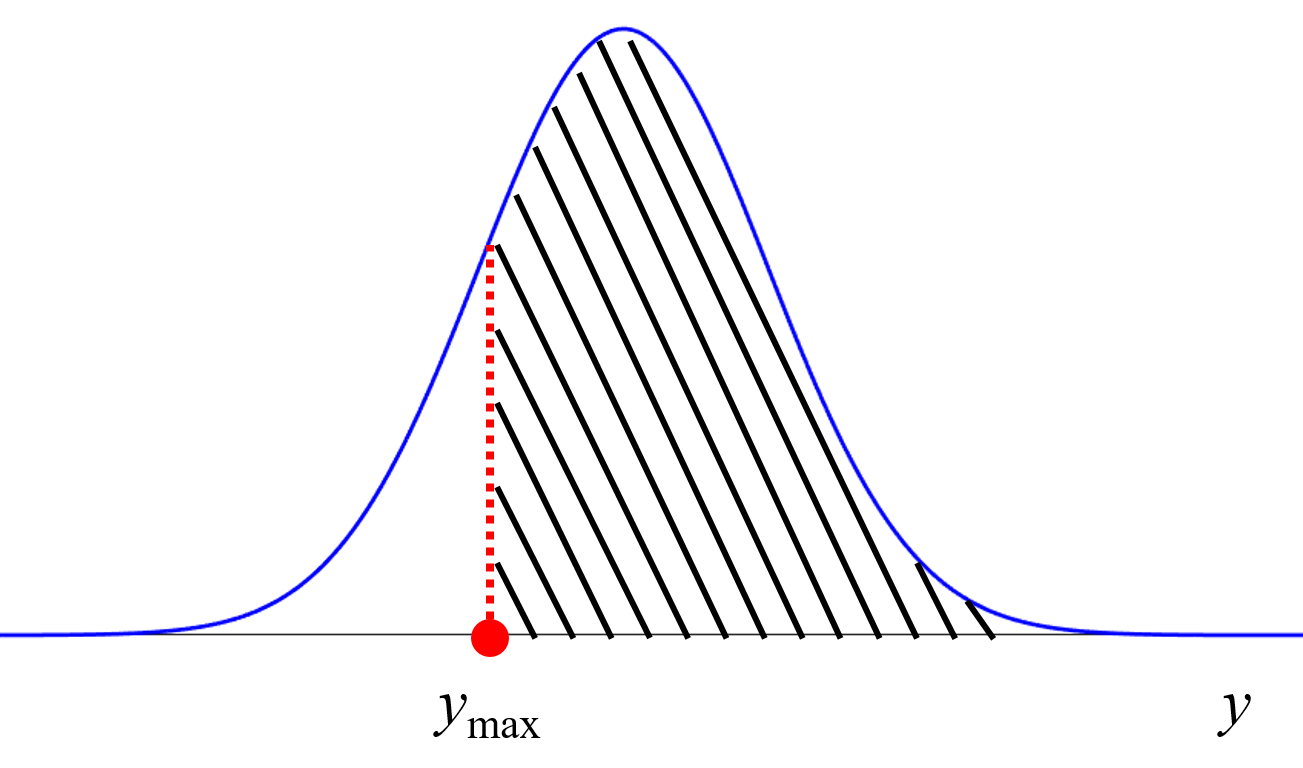
- 獲得関数の値が最大となる X の値の候補を 1 つ選択する
- 選択された候補の Y の予測値を実測値とみなして、データベースにサンプルを追加する
- 再度モデルを構築し、 1. に戻る
選びたい実験候補の数だけ、1. – 3. を繰り返します。基本的に、既存のサンプルに X の値が似ているものがあるときは、予測値の分散が小さくなりますので、選ばれにくくなることから、異なる X の値が選ばれやすくなります。
なお、選択された複数の候補の実験が終了したら (真の Y の実測値が得られたら)、Y の予測値のサンプルを削除します。

このようにすることで、一度に複数回の実験ができる状況でも、効率的にベイズ最適化を行えます。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。