分子設計・材料設計・プロセス設計・ソフトセンサーなどにおいて、データ解析をするとき、目的としては Y の値を予測することや Y の値が目標を達成する X の値を設計することです。そのため主な解析手法は回帰分析手法やクラス分類手法になります。
一方で、データの可視化もデータ解析の一つです。ヒストグラムや散布図、基礎統計量や相関係数によってデータの分布を確認します。もしくは主成分分析 (Principal Component Analysis, PCA) や Generative Topographic Mapping (GTM), t-distributed Stochastic Neighbor Embedding (t-SNE) などによって説明変数 X を低次元化します。

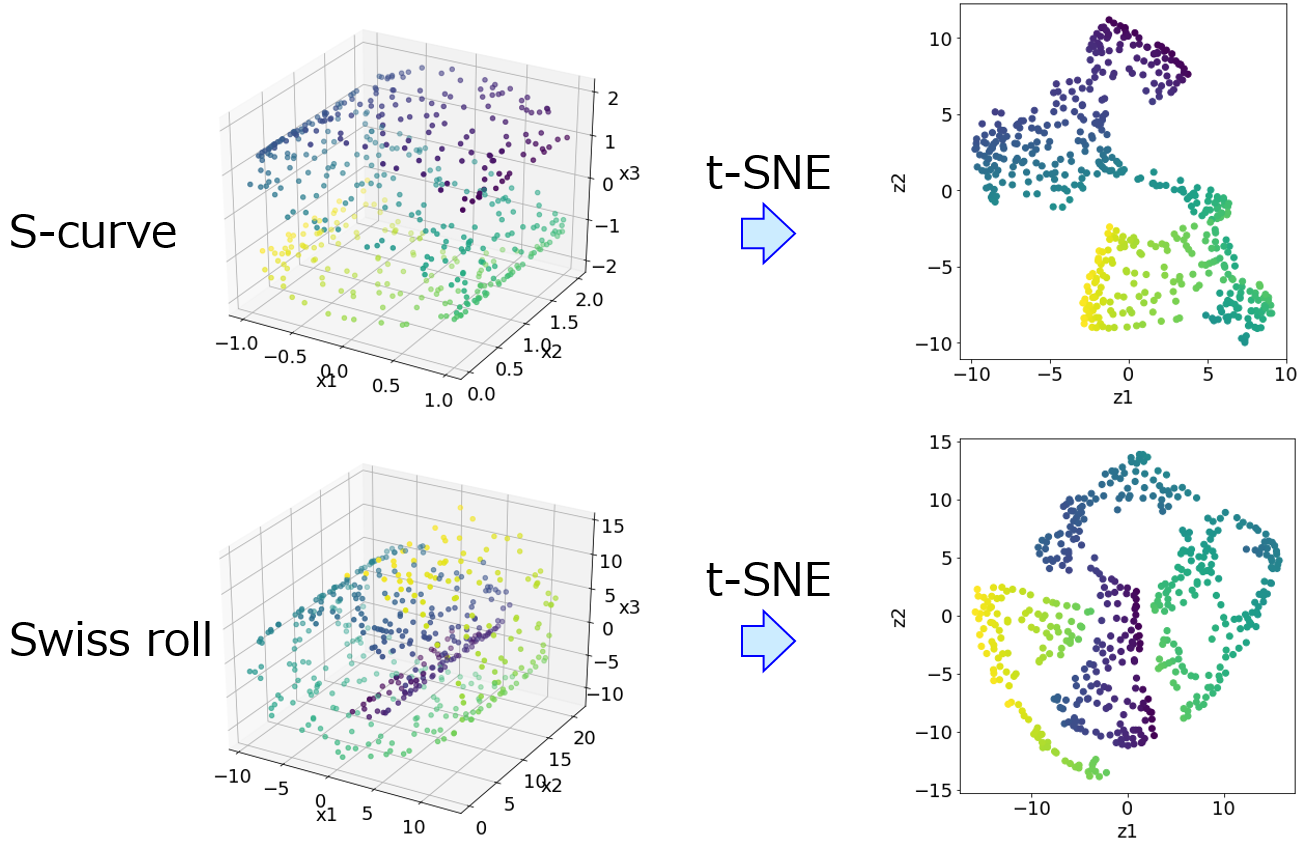
もちろんデータ解析の目的が、データの可視化であれば、積極的に上記の手法を用いて可視化すると思いますが、目的が先に書いたように Y の値の予測や Y の値が目標を達成する X の設計であるときには、データの可視化はやらなくてもよいように思われます。ただ、やはりデータの可視化には意味があります。ここではデータ解析におけるデータの可視化を行う理由についてお話ししたいと思います。
理由は大きく分けて3つあり、
- 外れ値検出
- 予測精度の高いモデル構築の検討
- 予測結果やモデルの逆解析の結果の議論
です。それぞれ説明します。
外れ値検出
外れ値について、例えば回帰分析を行った後に、実測値と推定値の間のプロットを見たときに、対角線から外れたサンプルがあることもあります。このとき、 Y の値がおかしいのか、それとも X の値がおかしいのか、考えると思います。データの可視化をして、データセットの中に外れ値がある可能性があることを認識することで、それらのうちどちらに要因があるのか検討することもできます。もちろん X はたくさんあることが多いため、低次元化した後にその空間において外れ値があるかどうかを考えます。
ただ、非線形の低次元化手法を用いたときに、低次元化した後の空間における外れ値が、実際の (X の) 空間においても外れ値とは限りませんので注意しましょう。PCA では軸の回転 (と反転) のみであり、低次元化した後の空間における外れ値は、実際の空間においても外れ値であることが保証されます。しかし、非線形手法ではその保証はありません。たとえ低次元化した後に外れ値を検出しても、実際の空間では外れ値でない可能性もありますので注意しましょう。
予測精度の高いモデル構築の検討
X の数が大きいとき、低次元空間に写像した後に、散布図を確認することがあると思います。そこのサンプルに対して、クラスごとに色をつけてサンプルをプロットしたり、回帰分析において Y の値の大きさに応じて色付けしてプロットしたりすることで、予測精度の高いモデルを構築できそうかの見通しをつけられます。散布図において、クラスごとに分布が分かれていたり、色 (Y の値) が連続的に変化していたりすると、データ解析はやりやすそうだと考えられます。また、そのような状況においても、予測精度の高いモデル構築に失敗したということは、X の多次元空間においてモデルがオーバーフィットした可能性が考えられます。このように予測精度の高いクラス分類モデルや回帰モデルを構築するための議論の材料になったりします。
予測結果やモデルの逆解析の結果の議論
先ほど散布図において、サンプルのクラスごとに色付けしたり、サンプルの Y の値に応じて色付けしたりするといったお話をしました。この図から、目的の Y の値を得たり、Y の値をさらに向上させたりするために、モデルの逆解析においてどちらの方向に X の値を設計すればよいかという指針がわかるかもしれません。また、モデルの逆解析によって生成されて Y の値が予測されたサンプルをその図に重ねてプロットすることで、逆解析の結果を検証することもできます。
Y1, Y2 のように Y が 2 つある際には、Y1 vs. Y2 の、元のデータセットや逆解析の結果でプロットを確認することで、逆解析によってパレート最適解が更新されたかどうかチェックできます。
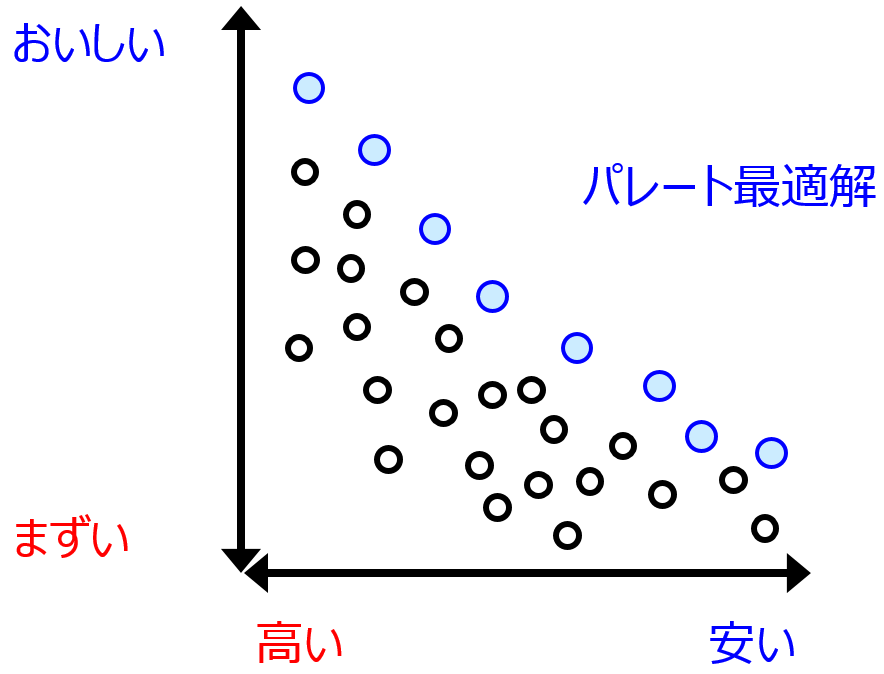
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


