世の中には、機能的なモノばかりではなく、機能的ではないけれども意味があるモノもあります。例えば、ろうそくです。昔は、空間を明るくするために使われていましたが、今は電球や蛍光灯がありますので、空間を明るくすることに関しては機能的ではありません。ただ、世の中からろうそくがなくなることはなく、ろうそくの火やその光が好きな人にとっては、なくてはならないモノです。その人にとっては、ろうそくは意味があるモノです。
自動車も年々高機能化していますし、自動運転車も検討されていますが、機能的には劣る昔の車 (クラシックカー) が好きで乗る人もいます。その人にとっては意味があるわけです。
データ解析・機械学習の分野でも、年々新たな手法が開発されているため、ひと昔前の手法に対して上位互換性をもつ手法もあります。例えば最小二乗法による線形重回帰分析 (Multiple Linear Regression, MLR) に対する Partial Least Squares Regression (PLS), リッジ回帰(Ridge Regression, RR), Least Absolute Shrinkage and Selection Operator (LASSO), Elastic Net (EN) です。
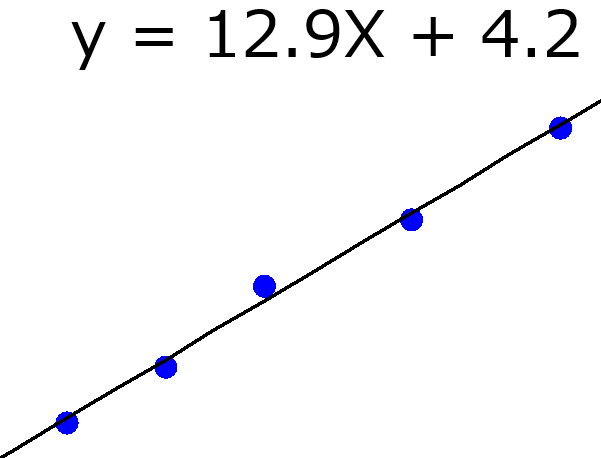
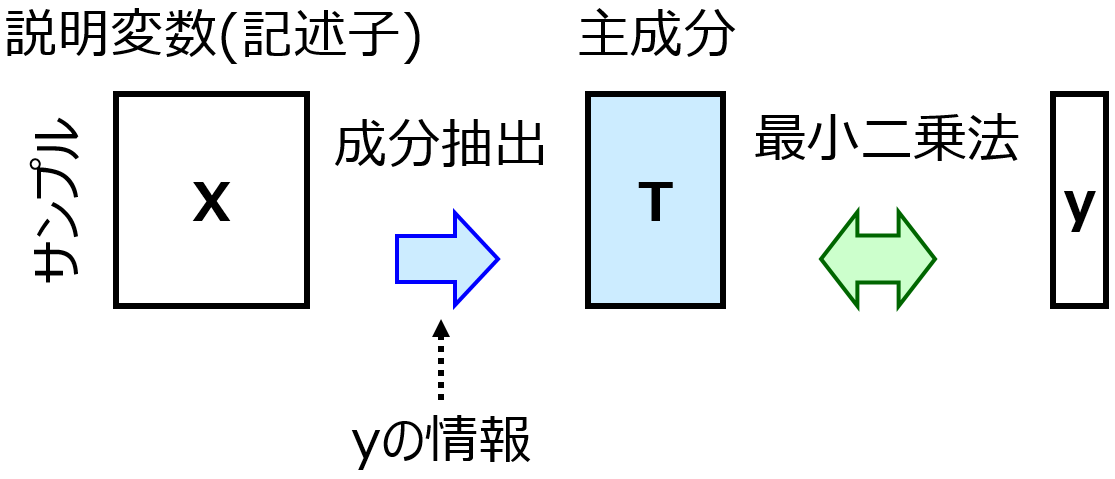
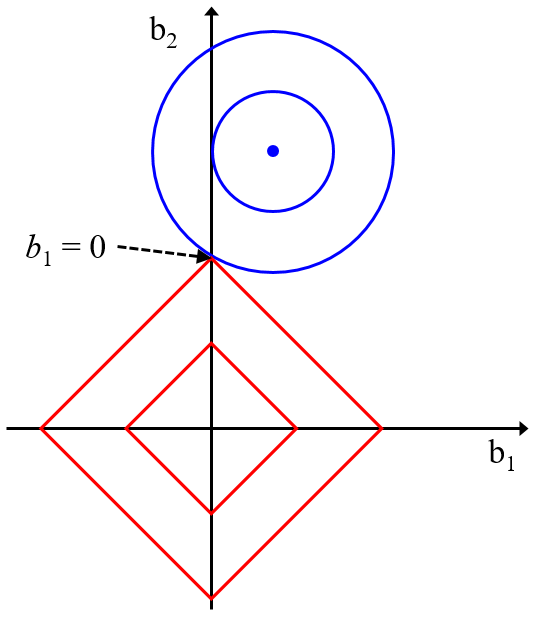
PLS, RR, LASSO, EN それぞれ、線形の回帰モデルを柔軟に設計できますし、ハイパーパラメータの値を調整することで MLR にもなります (PLS の成分数を最大値にしたり、RR, LASSO, EN の λ を 0 にしたりすると MLR と同じです)。ハイパーパラメータの値によって柔軟にモデルを設計できるわけです。
また、自己組織化マップ (Self-Organizing Map, SOM) に対して Generative Topographic Mapping (GTM) は上位互換性があります。

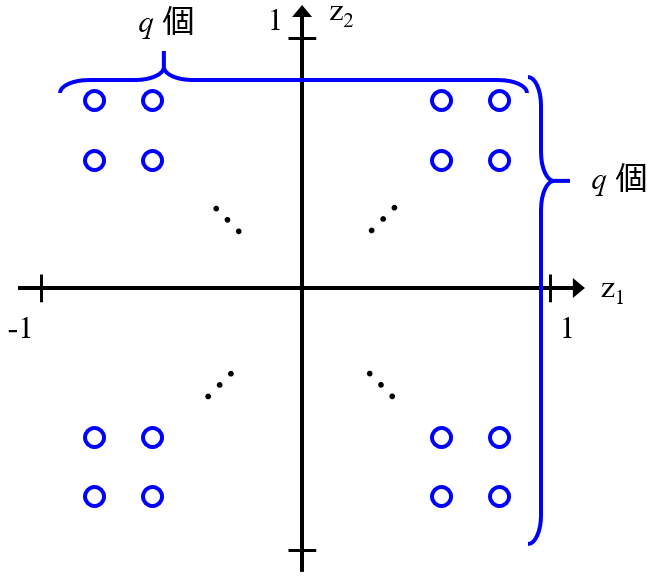
C. M. Bishop 先生が指摘しているように、SOM のいくつかの問題点を解決する形で、GTM が開発されました。そういう意味では、Y を含めた SOM である Counter Propagation Neural Network に対して Generative Topographic Mapping Regression (GTMR) も上位互換性をもつといえます。


k最近傍法 (k-Nearest Neighbor, k-NN) に対するサポートベクターマシン (Support Vector Machine, SVM) は微妙なところです。
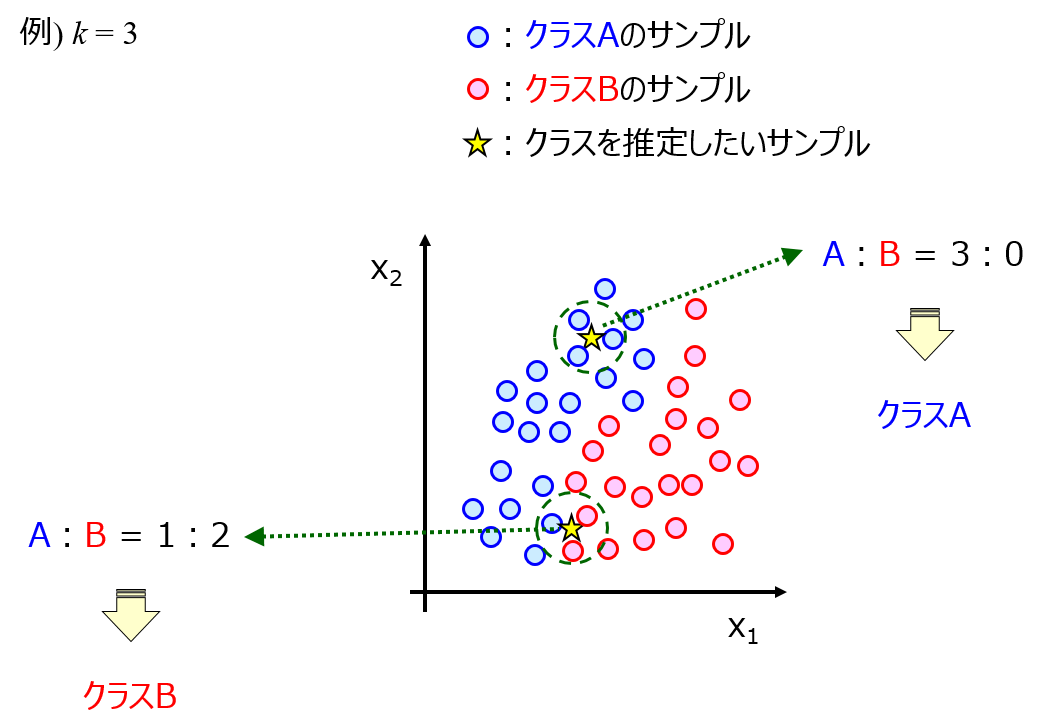
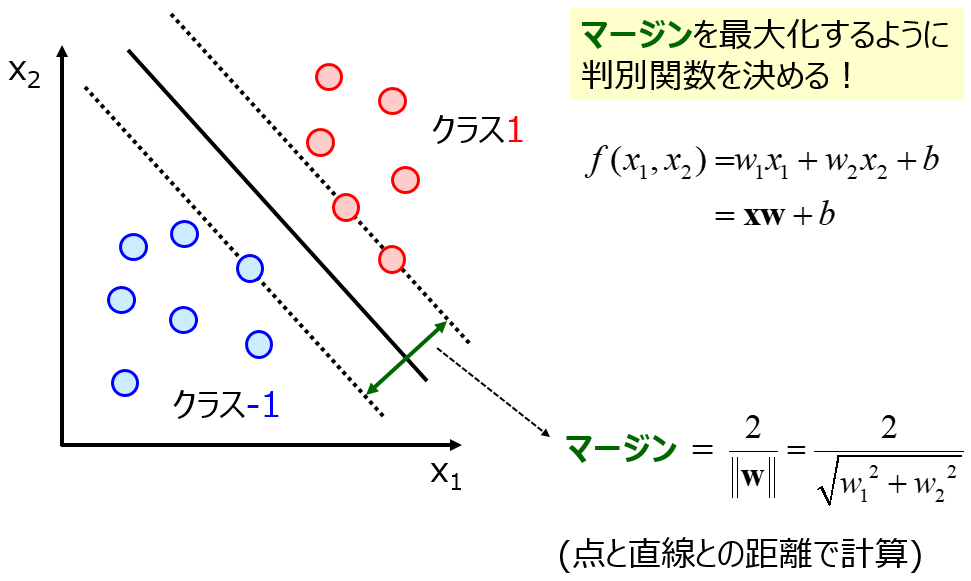

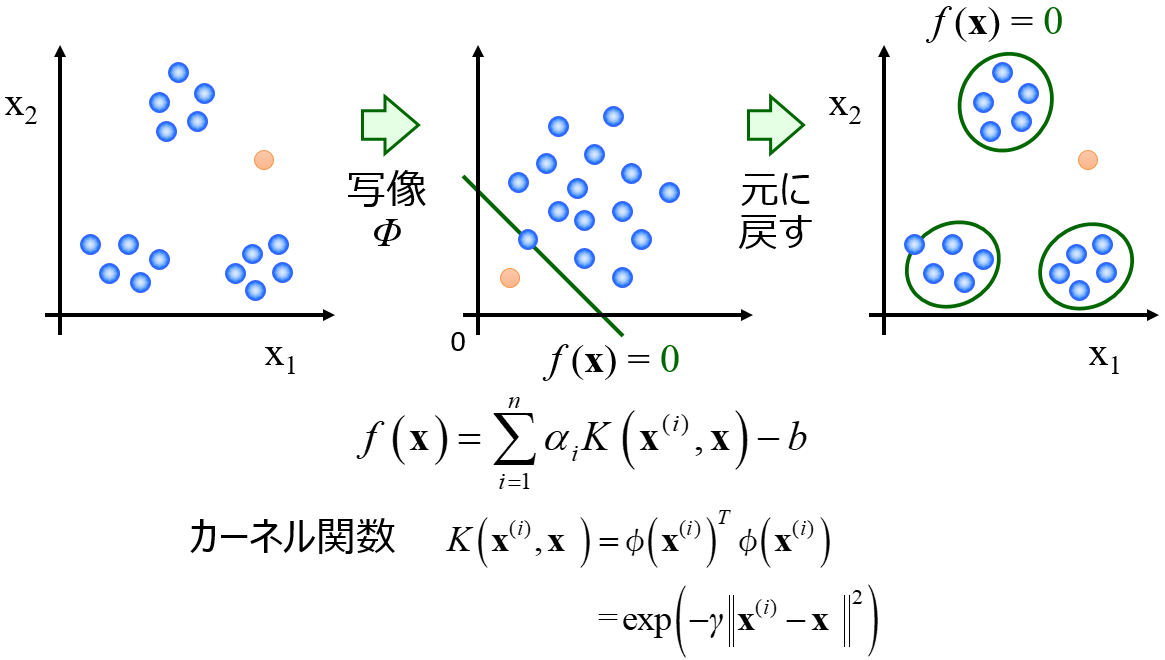
k-NN の k の値は設定しやすい一方で、SVM のハイパーパラメータは適切に設定できないと精度が下がってしまいます。また、k-NN ではサンプルの更新がしやすいです。完全な上位互換とはいえないかと思います。
では、私が例えば MLR をもう使わないか、PLS, RR, LASSO, EN にすべて置き換えるか、というと、そうではありません。MLR は、目的変数 Y の誤差が小さくなるように回帰モデルを構築する、といった原理原則を教えるのにとても有効です。私にとっては意味があるものです。また SOM も、データの可視化の原理原則である、実際の空間において近いサンプルが可視化した後の空間・平面でも近い必要があり、またその逆も満たす必要があることを教えるのに便利です。k-NN も Y の値が似ていたり、Y のカテゴリーが同じだったりするサンプル同士は、X の値も似ていること、またその逆のことも教えやすいです。
他の例でいえば、例えば PLS の 1 成分モデルでしょうか。1 成分しか用いませんので、多くの場合で推定性能は低く、機能性があるとはいえません。しかし、多重共線性のため線形回帰モデルの (標準) 回帰係数を説明変数 X の Y に対する寄与度とすることは危険ですが、PLS の 1 成分モデルであれば、もちろんその推定精度の範囲内において、回帰係数を X の Y への寄与度とすることができます。線形回帰分析の意味を変える手法といえるでしょう。
データ解析・機械学習の手法の中には、機能的な手法もあれば意味のある手法もあります (機能的でない手法にすべて意味があるというわけではありません)。色々な手法に触れて、一度は試してみるのがよいかもしれません。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


