説明変数 X と目的変数 Y との間でモデル Y = f(X) を構築するとき、特に Y が連続値の場合は回帰分析が行われます。回帰分析手法にはいろいろありますが、ここではガウス過程回帰 (Gaussian Process Regression, GPR) を取り上げます。

もちろん、他にも有効な回帰手法があることは最初に述べておきます。
とはいえ、DCE tool や DCE soft sensor にも搭載されているように
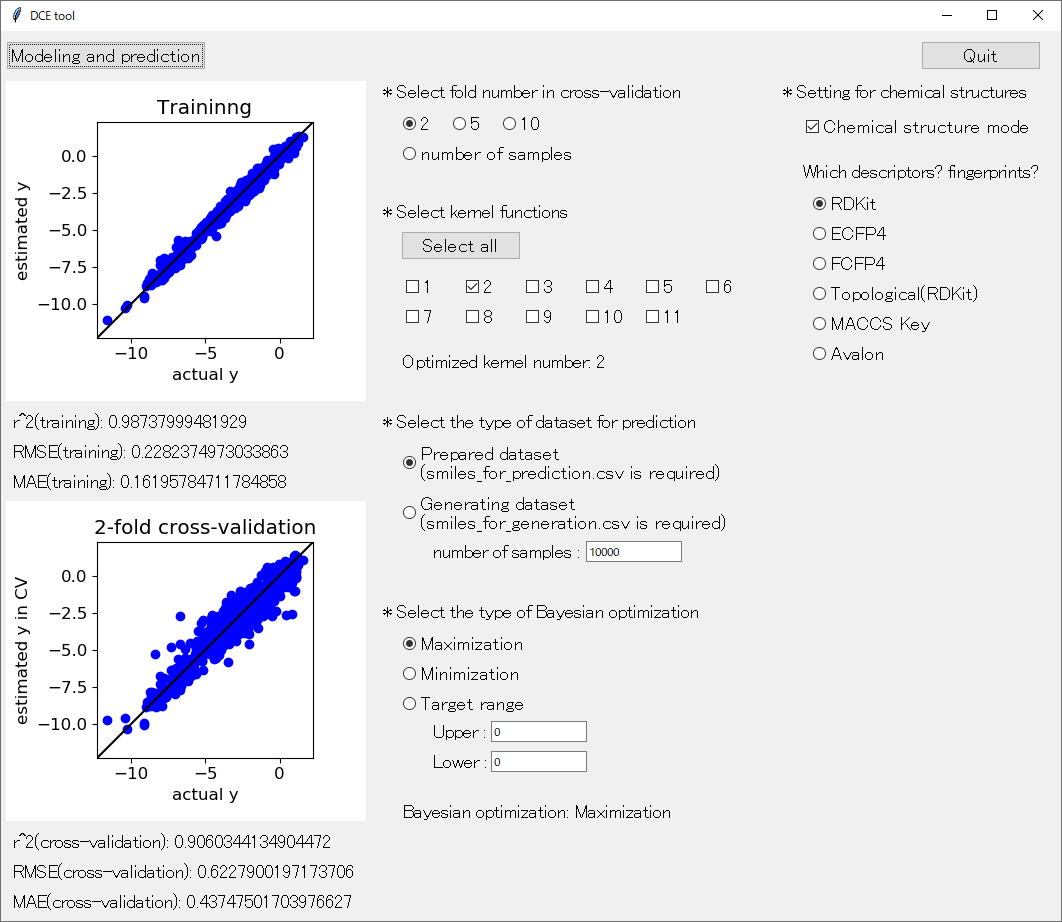
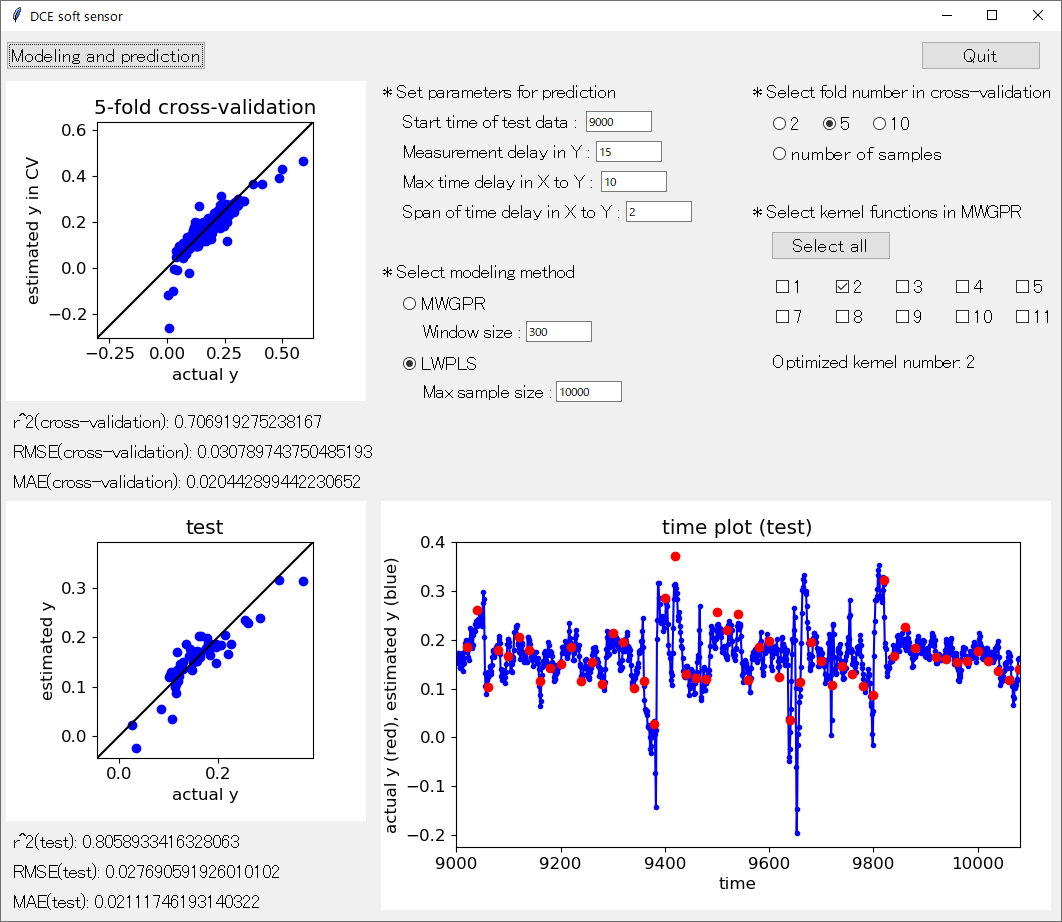
GPR はよく用いられる回帰分析手法の一つです。その理由は大きく分けて二つあります。
- 予測値だけでなくその分散を計算可能
- カーネル関数により柔軟にモデル選択が可能
GPR の使い方や注意点について述べながら、順に説明します。
一つ目の予測値だけでなくその分散を計算できる点についてです。モデルに X の値を入力して Y の値を予測すると同時に、その予測値の信頼性を議論できます。たとえば、分散の平方根である標準偏差を計算して用いることで、予測値が正規分布に従うと仮定すれば、予測値±標準偏差の2倍 以内に、およそ 95 %の確率で実測値が得られる、といったことがわかります。
このような特徴から、ソフトセンサーにおいて予測値のエラーバーを見積もるために使用できます。これによって装置やプラントにおけるプロセス状態ごとに、予測値の信頼性が変わることを定量的に評価できます。過去の運転状態から大きく変化したとき、予測値は信頼できないと考えられますし、過去の運転状態に近いようなプロセス状態であれば、予測値を信頼できます。このような議論を定量的にでき、エラーバーという形にして目で見て確認できます。
分子設計や材料設計においては、ソフトセンサーと同様にして、予測した物性値や活性値の信頼性を議論できるのはもちろんのこと、ベイズ最適化に応用できます。モデルの逆解析として、予測値とその分散を用いることで獲得関数を計算し、その値が大きいように、次に合成する分子や実験条件を選択できます。
GPR が用いられるもう一つの理由として、カーネル関数により X と Y の間の関係に柔軟に対応できることです。

GPR 以外にもサポートベクター回帰をはじめとして、カーネル関数と組み合わせられる手法はいろいろとありますが、GPR では Y が分布で表されることから最尤推定法に基づいてカーネル関数におけるパラメータ (ハイパーパラメータ) を決められます。ハイパーパラメータを決めるのにクロスバリデーションが必要ありません。そのためカーネル関数の中のハイパーパラメータの数が多くなっても、現実的な時間で最適化できます。
ただ、ハイパーパラメータ多くなればなるほど、オーバーフィッティング (過学習) の可能性は高くなります。基本的に GPR では、トレーニングデータの Y の実測値と予測値はほとんど同じ値になることが多いため、クロスバリデーション (内部バリデーション) や外部バリデーション (テストデータとトレーニングデータに分けて検証) によってカーネル関数ごとにモデルの予測性能をしっかり評価しながら、カーネル関数を選択する必要があります。さらに、データセットとカーネル関数の組み合わせによっては、逆解析をするとき、様々な仮想サンプルを入力したときに Y の予測値がほとんど一定になってしまうこともあります。このようなことにも注意しながら、カーネル関数を利用するとよいでしょう。
また GPR では、特に X の値が同じで Y の異なるサンプルがあると、以下の p.36 における分散共分散行列の逆行列が不安定になることがあります。

どのカーネル関数を用いても Y の予測値が一定になったり変な値になったりする場合は、それらのサンプルの Y の平均値を用いて、一つのサンプルに統合したほうがよいです。
今回は非常に有用な回帰分析手法である GPR について使い方やその注意点についてお話しました。クラス分類においても、Y をダミー変数にすることで GPR を応用可能です。ぜひ活用されてはいかがでしょうか。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


