正則化項により過学習(オーバーフィッティング)を防ごう！

回帰モデルを構築するとき、過学習 (オーバーフィッティング) が問題になります。ここではリッジ回帰・LASSO・Elastic Net といった正則化項を用いる手法を例にして、

リッジ回帰(Ridge Regression, RR), Least Absolute Shrinkage and Selection Operator (LASSO), Elastic Net (EN)～誤差の二乗和と一緒に回帰係数の値も小さくする～

リッジ回帰(Ridge Regression, RR), Least Absolute Shrinkage and Selection Operator (LASSO), Elastic Net (EN) について、pdfとパワーポイントの...

最小二乗法による線形重回帰分析との関係や、オーバーフィッティングを防ぐメカニズムを説明します。

最小二乗法による線形重回帰分析では、線形のモデル y = a₁x₁ + a₂x₂ + ・・・を仮定して、目的変数 y の誤差の二乗和が最小になるように、回帰係数 a₁, a₂, … を決めます。

(y の誤差の二乗和)

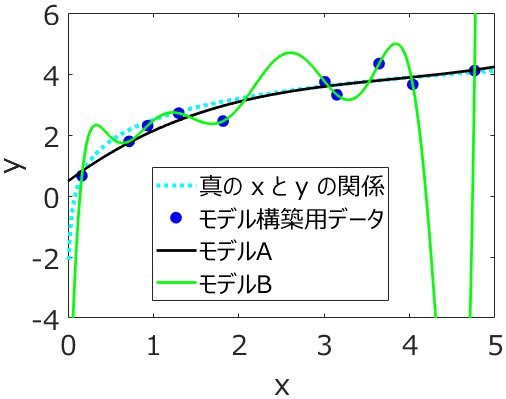
この方法によって、y の誤差が小さくなる回帰係数を求めることはできますが、オーバーフィッティングが生じてしまうこともあります。つまり、トレーニングデータのサンプルに対しては y の誤差が小さくなりますが、それら以外のサンプルに対して誤差が大きくなってしまう、ということです。

このオーバーフィッティングと関係することとして、回帰係数の絶対値が大きくなることが挙げられます。こちらに具体例があります。

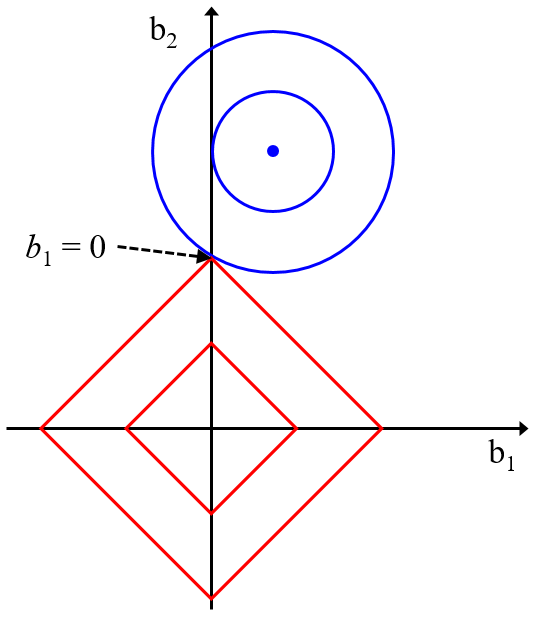
人工知能・機械学習のときには過学習 (オーバーフィッティング) に気をつけよう！～過学習とその対処法～

応化先生と生田さんが過学習 (オーバーフィッティング) について話しています。応化：今日は過学習についてです。生田：過学習？学習し過ぎるってこと？応化：その通りです。生田：だったら悪いことじゃなさそうに聞こえるけど・・・。学習をたく...

そのため、回帰係数の絶対値を小さくすることでオーバーフィッティングを防げるだろうということで、正則化項が出てきました。この正則化項は、回帰係数の大きさに関する項です。y の誤差の二乗和だけでなく、回帰係数の大きさも小さくすることで、オーバーフィッティングを防げるだろう、ということです。そのためリッジ回帰・LASSO・Elastic Net では以下の式を最小化する回帰係数を計算します。

(y の誤差の二乗和) + (重み) × (回帰係数の大きさ)

リッジ回帰・LASSO・Elastic Net それぞれ、(回帰係数の大きさ) の項が異なります。そしてうまく (重み) を調整することで、(y の誤差の二乗和) と (回帰係数の大きさ) の両方がいい塩梅で小さくなるように、回帰モデルを構築することが目的になります。

もちろん、トレーニングデータにおける y の誤差が小さくなるように (重み) を決めてしまうと、(重み) = 0、すなわち最小二乗法による線形重回帰分析とまったく同じになってしまいます。そのため、y の誤差の二乗和を計算したデータ以外のデータを用いて、(重み) を決める必要があります。よく使われるのがクロスバリデーションです。

回帰モデル・クラス分類モデルを評価・比較するためのモデルの検証 (Model validation)

いろいろな回帰モデル・クラス分類モデルを構築したり、モデルの中のハイパーパラメータ (PLSの成分数など) を決めたりするとき、モデルを評価・比較しなければなりません。そのためのモデルの検証 (model validation) の方法につ...

クロスバリデーション後の y の予測誤差が最小になる (重み) の値にすることで、予測精度を考慮して (重み) を決めることができます (もちろん結果的に (重み) = 0 になることもあります)。このようにして、回帰係数を決めるときのデータ以外のデータを予測できるような、正則化項の重みを決め、オーバーフィッティングを防ごうというわけです。

ちなみに、サポートベクター回帰 (Support Vector Regression, SVR) もリッジ回帰・LASSO・Elastic Net の仲間といえます。