「Pythonで学ぶ実験計画法入門 ベイズ最適化によるデータ解析」 をご購入いただき感謝申し上げます。売れ行きも好調のようで嬉しい限りでございます。多くの方々に実験計画法、適応的実験計画法、ベイズ最適化をご活用いただきたいという思いで執筆した本であり、たくさんの方に本書を手にとっていただけますと幸いです。


そんな中、出版社経由や金子研オンラインサロン、そして Github において、すでにお読みいただいた方々から、ご質問やご指摘をいただいております。感謝申し上げます。そこでいただいたご指摘から、間違えがあることもわかりましたので、正誤リストとして以下にまとめます。申し訳ございませんが、よろしくお願いいたします。もちろん、間違いについては重版がかかるごとに修正してまいりますし、GitHub のサンプルプログラム https://github.com/hkaneko1985/python_doe_kspub は修正後の最新版になっております。
p.5 上から 8, 9 行目
(誤) このように、実験するになら現実的に不可能な数の化学構造でも、
(正) このように、実験するには現実的に不可能な数の化学構造でも、
p.18 下から 10, 11 行目
(誤) ベイズ最適化を用いることで、1.4 節で説明したほうなメリットが得られます。
(正) ベイズ最適化を用いることで、1.4 節で説明したようなメリットが得られます。
p.24 サンプルプログラム3行目
(誤) variable_number = 0 # ヒストグラムを描画する特徴量の番号
(正) number_of_variable = 0 # ヒストグラムを描画する特徴量の番号
p.47 サンプルプログラム
(誤) autoscaled_estimated_y_in_cv = cross_val_predict(model, autoscaled_x, autoscaled_y) # y の推定
(正) autoscaled_estimated_y_in_cv = cross_val_predict(model, autoscaled_x, autoscaled_y, cv=cross_validation) # y の推定
p.55 下から 1, 2 行目
(誤) IPython コンソール (8.4節参照) に、トレーニングデータにおける r2, RMSE, MAE (図 3‑32、図 3‑33)、
(正) IPython コンソール (8.4節参照) に、トレーニングデータにおける r2, RMSE, MAE (図 3‑32)、
p.77 式(3.74)
(誤)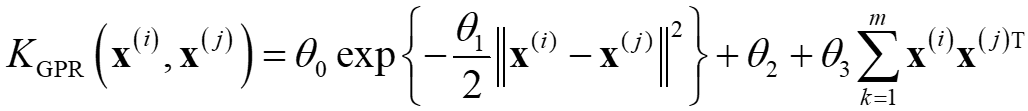
(正)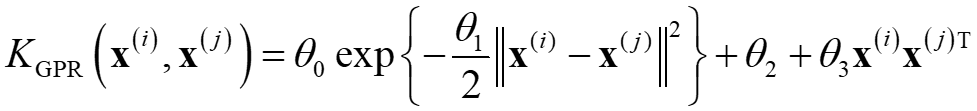
p.79 下から 2, 3 行目
(誤) このとき式(8.84)で求めたい、p(yobs(n+1) | yobs) の平均をμ(x(n+1))、分散をσ2(x(n+1)) したとき、
(正) このとき式(8.84)で求めたい、p(yobs(n+1) | yobs) の平均をμ(x(n+1))、分散をσ2(x(n+1)) としたとき、
p.88 上から 9, 10 行目
(誤) AD 内のサンプルと AD 外のサンプルとをが分離しにくくなってしまいます。
(正) AD 内のサンプルと AD 外のサンプルとを分離しにくくなってしまいます。
p.104 サンプルプログラム16行目
(誤) converted
(正) converted * desired_sum_of_components
p.106 サンプルプログラム5行目 [x_generated = pd.read_csv(‘generated_samples.csv’, index_col=0, header=0)] の次の行に以下を追記
autoscaled_x_generated = (x_generated – x_generated.mean()) / x_generated.std()
p.106 サンプルプログラム14-16行目
(誤)
# 2. オートスケーリングした後に D 最適基準を計算
autoscaled_new_selected_samples = (new_selected_samples – new_selected_samples.mean()) / new_selected_samples.std()
xt_x = np.dot(autoscaled_new_selected_samples.T, autoscaled_new_selected_samples)
(正)
# 2. D 最適基準を計算
xt_x = np.dot(new_selected_samples.T, new_selected_samples)
p.118 式(5.6)
(誤) 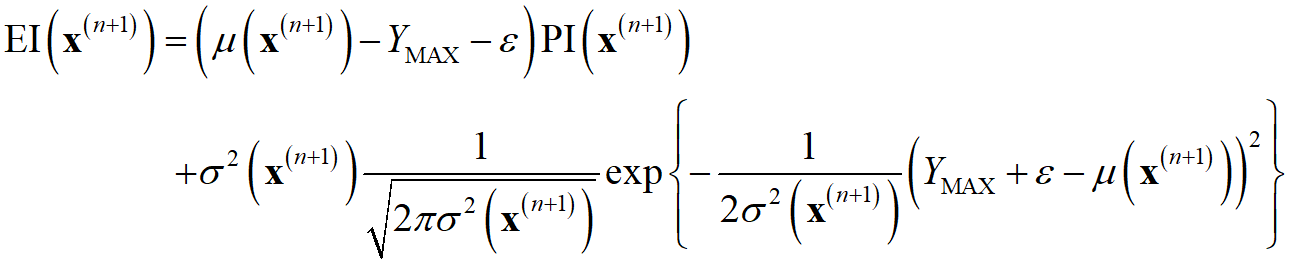
(正) 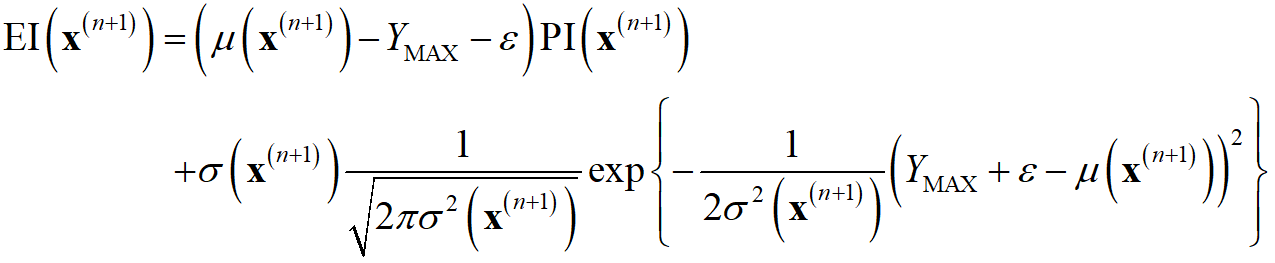
p.149 上から 1 行目
(誤) ここで p(x | y, μy,i, Σyy,i) は X の推定値における i 番目の正規分布を意味し、
(正) ここで p(x | y, μy,i, Σyy,i) は、X の推定結果を表す混合正規分布における i 番目の正規分布を意味し、
p.156 上から三行目 式(8.18)
(誤)
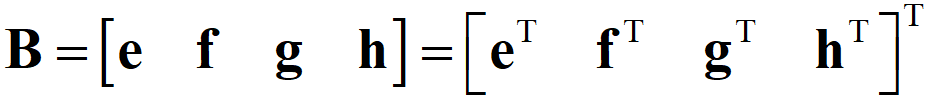
(正)
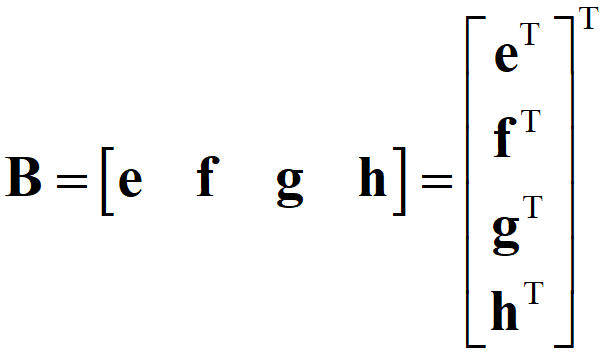
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


