金子研で開発している直接的逆解析についてです。
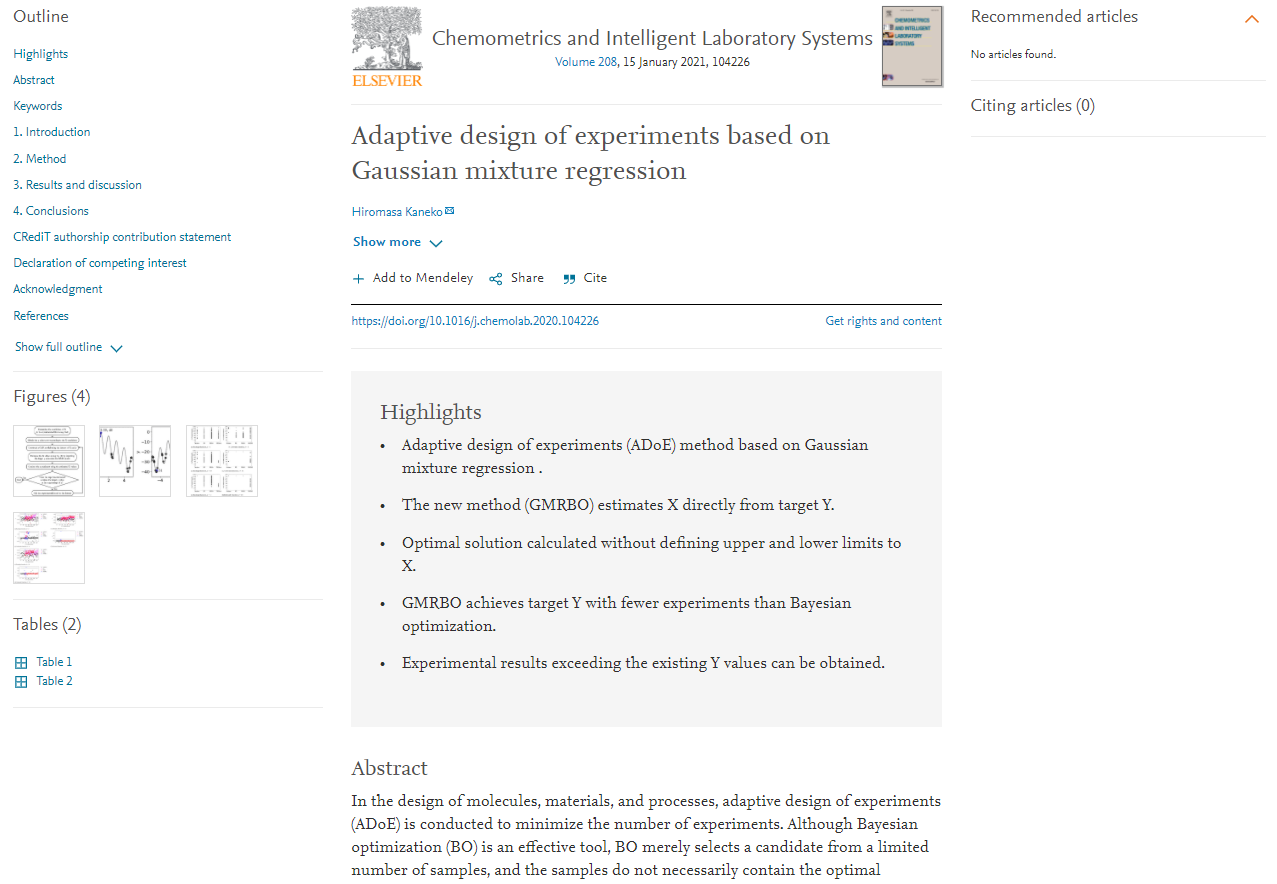
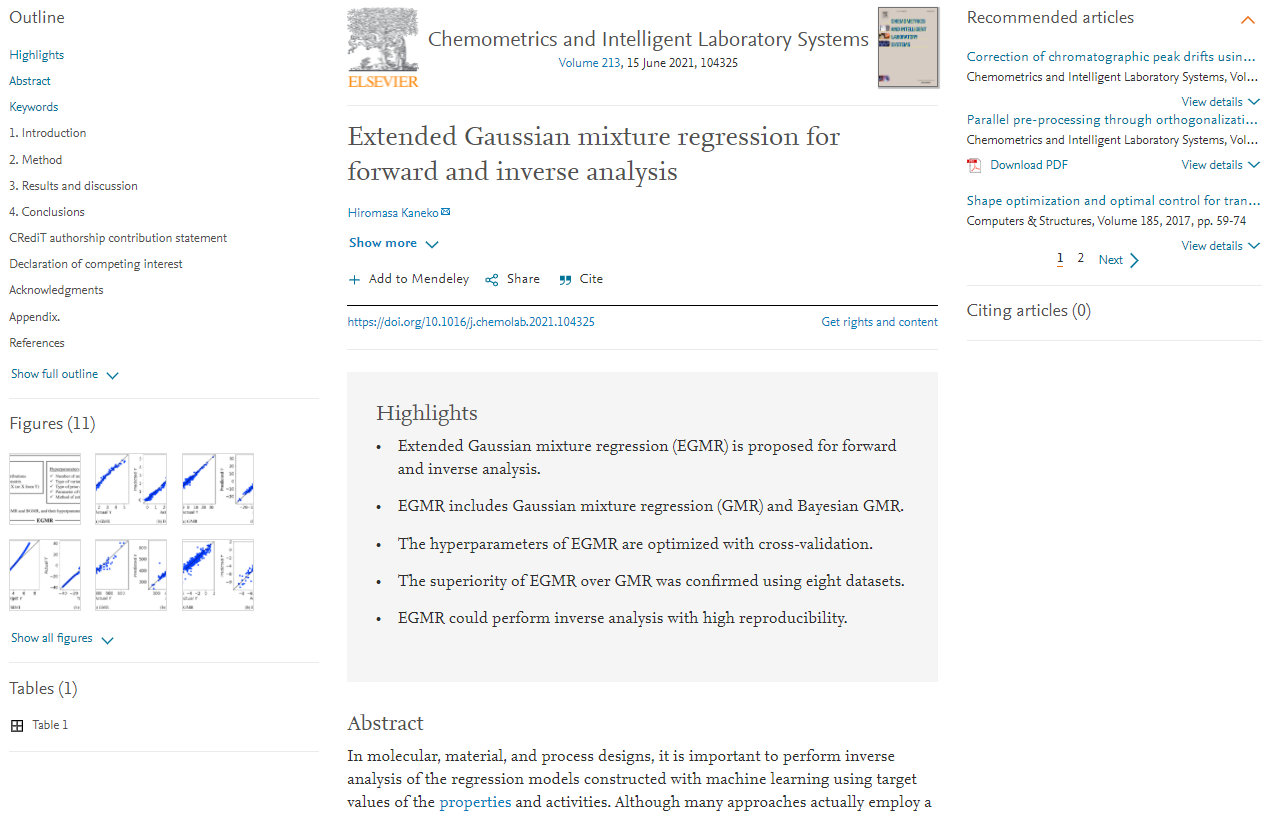

(直接的逆解析ではない) いわゆる一般的な逆解析では、モデルを構築した後に、説明変数 x の大量のサンプルを生成し、構築したモデルに入力し、目的変数 y の値を予測します。そして予測値が良さそうな x のサンプルを選択します。ベイズ最適化も、y の予測値が獲得関数の値に変わるだけで、基本的な流れは同じです。このように一般的な逆解析は、「逆」 解析とはいえ、順解析をたくさん繰り返す擬似的な逆解析といえます。大量のサンプルを生成していますが、すべての x の空間を探索できているわけではありません。もちろん遺伝的アルゴリズムなどの最適化アルゴリズムにより、探索を効率化することはできますが、そもそも x の空間が壮大であるため、すべてを探索することは困難です。また、擬似的な逆解析では、サンプル生成のとき、x にあらかじめ上限や下限を設定する必要があるため、その上限や下限を超えた結果は得られない、すなわち y の予測値が既存のデータを超越した結果は得られにくいといった特徴もあります。
一方、金子研で開発している直接的逆解析では、文字通り y の目標値から直接的に x の値を計算できます。x の値に上限・下限といった制限を加えることなく、y の値を達成する確率が最も高い x の値を解析的に求めることができます。Gaussian Mixture Regression (GMR) や Generative Topographic Mapping Regression (GTMR) で直接的逆解析を行うことができます。
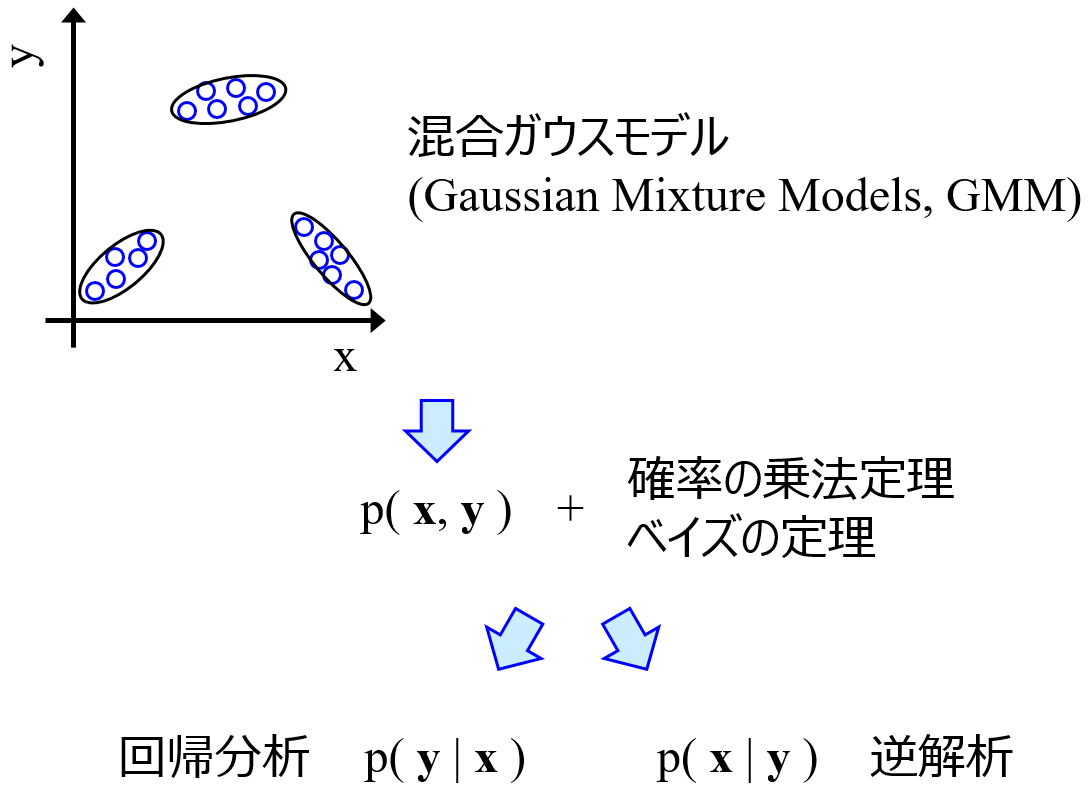

もし興味ある方は、DCEKit でこれらの手法による直接的逆解析をお試しいただけると幸いです。

直接的逆解析ができても、実験装置の制約等で、例えば温度を何℃以上にできないなど、特徴量に制約がある場合もあります。また、実験コスト・製造コストなどの背景により、特徴量によってはある値に固定したい、といった制約もあります。
もちろん直接的逆解析のメリットの一つは、x に上限・下限を設けることなく逆解析を達成できることですが、逆に、x に制約を与えることも簡単にできます。やり方としては、y の目標値と一緒に、制約のあるいくつかの x に対して制約の値をモデルに入力します。直接的逆解析をする GMR や GTMR では x と y の区別はありません。モデルにおいては、すべての特徴量の間の関係が構築されており、一部の特徴量の値を固定すると、それ以外の特徴量の確率密度分布が求まる、といった仕組みになっています。そのため、y の目標値を固定すると、それ以外の特徴量である x の確率密度分布を求められるのですが、y だけでなく、いくつかの x についても合わせて、値を入力することで、それら以外の x の値を計算することができます。このように、y の値だけでなく制約のある x の値も入力することで、その x が制約の中での、それ以外の x の値を計算できます。
この考え方で、定性的な x を含む逆解析についても対応できます。基本的には、定性的な特徴量はダミー変数 (0 or 1 の特徴量) に変換して x とし、モデル構築が行われます。直接的逆解析でも同様にしてモデルを構築しますが、普通に y の値を入力するだけでは、x が 0, 1 以外の値となってしまいます。そこでダミー変数の x については、 y の値と一緒に、0 もしくは 1 を入力します。これにより、ダミー変数の x が 0 もしくは 1 のときの、それ以外の x の値を計算できます。ダミー変数の x が 0 と 1 の両方の場合で、結果を確認するとよいでしょう。
こちらの転移学習では、

データセットに 0 を追加して工夫することで、異なるデータセットを転移させて学習することができます。このようなデータセットの形式で構築されたモデルを直接的逆解析するとき、y の値を入力すると本来は 0 であるべき特徴量の x でも、0 以外の値になってしまいます。そこで、0 であるべき一部の x については、y の目標値と一緒に 0 を入力します。これにより、0 でなくてよい x の値を計算できます。
以上のようにして、直接的逆解析ではやり方を少し工夫することで、x の制約、定性的な x、転移学習を扱うことができます。ぜひご活用いただけますと幸いです。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


