金子研の論文が Journal of Computer Chemistry, Japan に掲載されましたので、ご紹介します。タイトルは
です。これは修士卒の清水 直斗さんが修士のときに取り組んだ研究の成果です。
基本的には、モデルの予測精度と解釈可能性はトレード・オフの関係にあります。
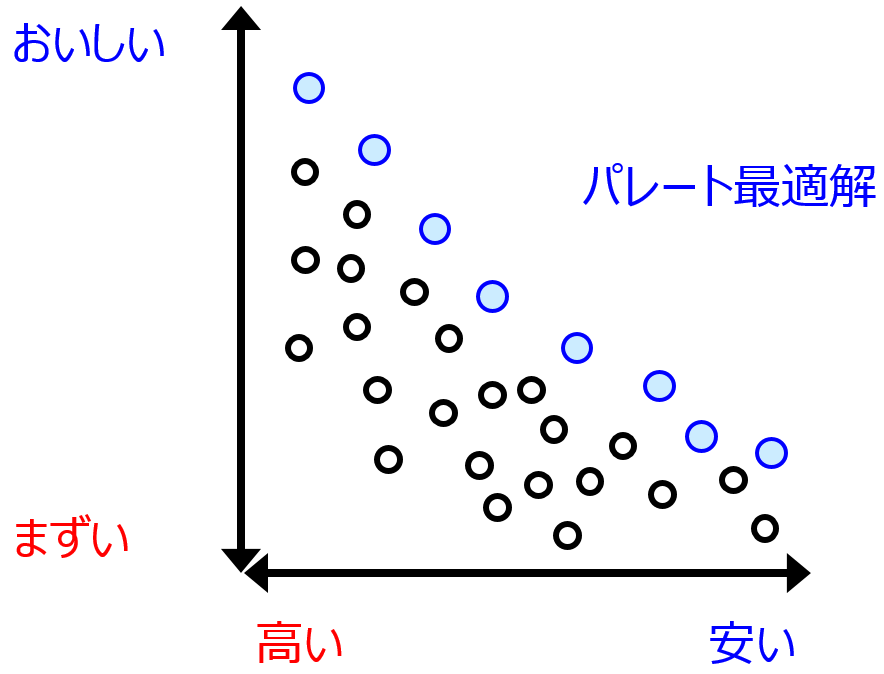
すなわち、(オーバーフィッティングが起こらないように気をつけて) モデルを複雑にして予測精度を上げようとすると、モデルの解釈は難しくなります。モデルをシンプルにして解釈可能性を上げようとすると予測精度は下がります。
ただ、モデルをシンプルにすると解釈可能性が上がるとはいえ、線形回帰分析をしたときの回帰係数を説明変数 x の目的変数 y への寄与度とすることが危険なのは、こちらに書いた通りです。

そこでランダムフォレストの変数重要度に着目しています。
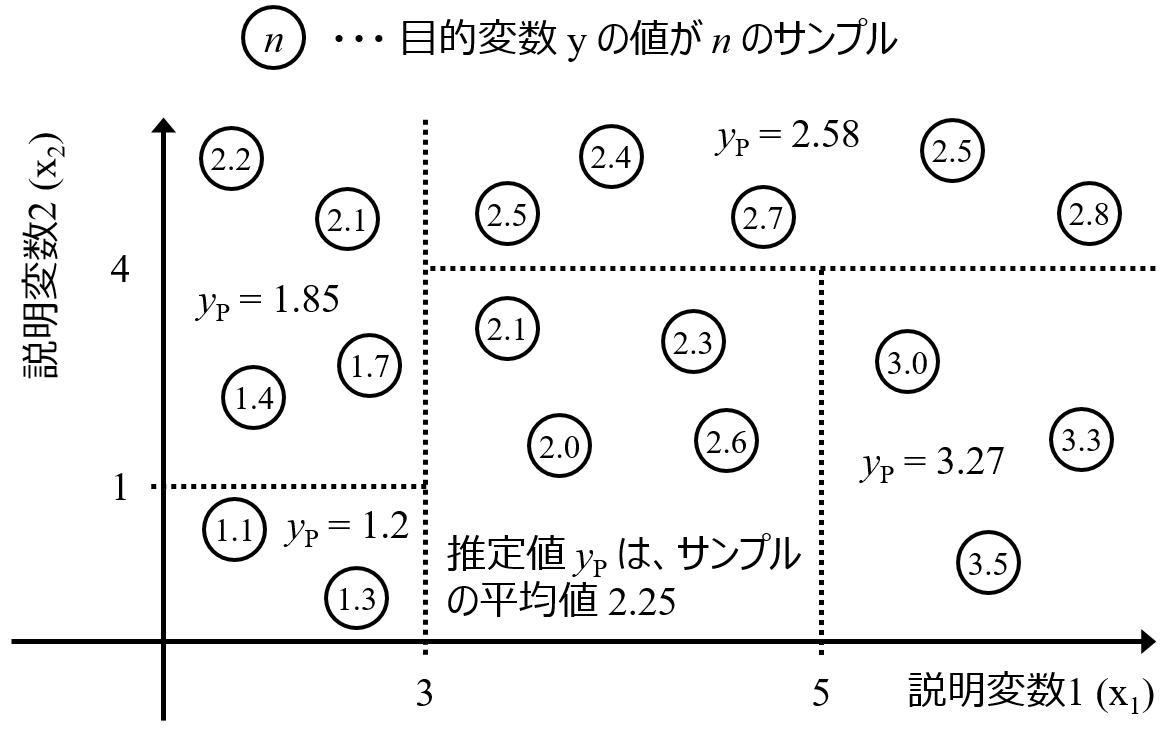
ただ、ランダムフォレストの変数重要度はデータセット全体で計算されたものであるため、データセットにおける全体的な傾向は捉えることはできますが、局所的な傾向、例えば y の値が大きいときにさらにその値を大きくするためにはどの変数が重要か、といったことは議論できません。さらに、”重要度” では、もちろん重要性は議論できますが、y の値を向上させるための、x の値の方向性はわかりません。
そこで、決定木とランダムフォレストを組み合わせた手法を提案しました。この手法では、決定木モデルを構築します。
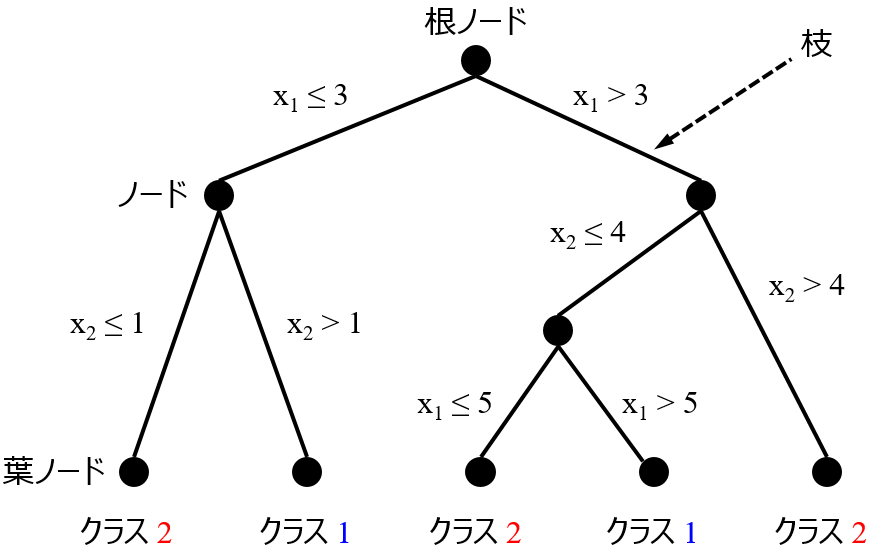
決定木では x の分岐によって y の大小が異なるといった形式でモデルが表現されるため、各 x とその値がしきい値より大きいか小さいか、によってモデルを解釈できます。ただ決定木は、モデルが単純であるがゆえに予測精度は低いです。そこで決定木の各葉ノードのサンプルのみを用いて、ランダムフォレストモデルを構築します。これにより予測精度を向上させることができます。さらに、決定木モデルによってデータセット全体を解釈し、y の大小である程度分割された上で、ランダムフォレストの重要度を求めることができます。つまり、葉ノードごとのランダムフォレストの変数重要度により、x の局所的な特徴を捉えることができるわけです。
論文では、提案手法を沸点のデータセット、水溶解度のデータセット、超伝導体のデータセットを用いて、モデルの予測精度や解釈可能性について議論し、良好な結果であることを確認しました。
興味のある方は、ぜひ論文をご覧いただければと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。