言葉の似ているクロスバリデーションとダブルクロスバリデーションですが、意味合いが異なります。

目的の違いとして、クロスバリデーションの目的は PLS における主成分の数や SVR における C, ε, γ といったハイパーパラメータを最適化することです。
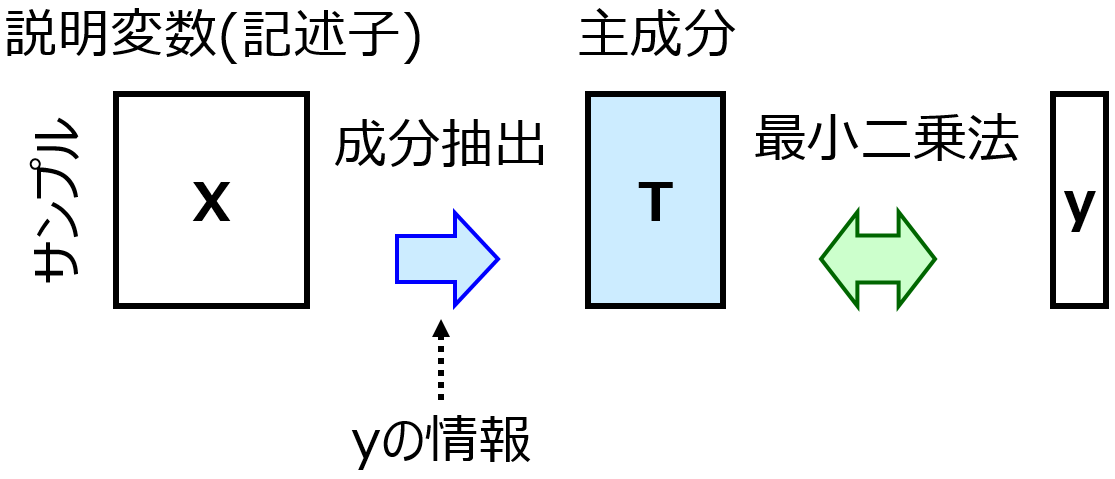

ハイパーパラメータの候補を変えながらクロスバリケーションを行い、クロスバリデーション後の予測性能が最も高いハイパーパラメータの候補を選択します。一方で、ダブルクロスバリデーションは手法を選択するために用います。PLS や SVR といった手法ごとにダブルクロスバリデーションを行い、ダブルクロスバリテーション後の予測精度を比較して最も高い手法を使用します。
この手法の比較のために、どうしてクロスバリデーションを使用してはいけないかというと、手法ごとにハイパーパラメータの候補の数に差があるためです。主成分の数しかハイパーパラメータがない PLS に比べて、三つのハイパーパラメータのある SVR の方が、ハイパーパラメータの候補が多く、そのたくさんの候補の中から、クロスバリデーションの結果がベストな候補を選択できるため、PLS のクロスバリデーションの予測精度と比較して、SVR のクロスバリデーションの予測精度の方が上がりやすいです。そのためクロスバリデーションは手法の比較に使用することはできません。
一般的に手法の比較は、データセットをトレーニングデータとテストデータに分割して、トレーニングデータを用いてクロスバリデーションでハイパーパラメータを最適化してからモデルを構築し、テストデータを予測してその予測性能を評価しますが、ダブルクロスバリデーションはその方法の代わりに、特にデータセットのサンプル数が小さいときに使用します。
なおダブルクロスバリデーションの中でクロスバリデーションが行われており、ダブルクロスバリデーションでは (用いているデータセットで) ハイパーパラメータの最適化を適切に行える手法かどうかも、ダブルクロスバリデーションでは評価されます。あくまでトレーニングデータとテストデータに分けてテストデータで評価することや、ダブルクロスバリデーションは手法間で比較するときに使用します。
ただし、ダブルクロスバリデーション = クロスバリデーションとなるときがあります。それは手法のハイパーパラメータがないときです。ハイパーパラメータがなければ、ハイパーパラメータの最適化にクロスバリデーションを使用する必要がありません。そのためダブルクロスバリデーションの中でクロスバリデーションをしなくなるため、クロスバリデーション = ダブルクロスバリデーションとなります。例えば、OLS ではハイパーパラメータがありませんので、ダブルクロスバリデーション = クロスバリデーションになります。
また、GPR でもカーネル関数を一つ決めてしまえば、他にパラメータありますが、クロスバリデーションではなく、最尤推定法により求められるため、ダブルクロスバリデーション = クロスバリデーションになります。

つまり、OLS やカーネル関数が決まっている GPR においてクロスバリデーションで予測精度を評価することで、他の手法におけるダブルクロスバリデーションによる評価結果と同等に比較できるわけです。
以上のクロスバリデーションやダブルクロスバリデーションの特徴をふまえて、それぞれの目的や使用用途について理解が深まると幸いです。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


