分子設計・材料設計・プロセス設計において、分子記述子・合成条件・製造条件・プロセス条件などの説明変数 x と物性・活性・特性などの y との間で数理モデル y = f(x) を構築して、x の値から y の値を予測したり、y が目標の値となる x の値を設計したりします。y の目標値が、既存のデータセットの最良値から遠いときには、ベイズ最適化を用いることで効率的に外挿を探索できます。


分子設計・材料設計・プロセス設計におけるベイズ最適化では、y に目標範囲があることが多くあります。ガウス過程回帰の予測値と分散によって定義される正規分布を、y の目標範囲で積分した値 (面積の大きさ) を獲得関数の値とすることで、その値が大きい x の値を選択します。
y が任意の値 (マイナス無限大から無限大、−∞ ~ ∞) となる可能性があるときは、これで問題ないですが、例えば y が原理的に0以下にならないときや、y が 0 から 1 の範囲にしか入らないときなど、y に取り得る範囲があるときには、積分した値を適切に獲得関数とみなすことができません。例えば、y が原理的に0以下にならないときに y を 0 から 0.01 の範囲にしたい場合とき、0 から 0.01 までの範囲で積分することが考えられますが、正規分布としては y が 0 以下のところにも裾野が伸びており、実際には 0 以下にならないのに、そうなる確率的には 0 ではない、いうことになってしまいます。−∞ から 0.01 で積分しても、実際には 0 以下にはならないにもかかわらず、その確率が考慮されてしまいます。y が 0 から 1 の範囲にしか入らないときも同様にして、0 以下や 1 以上のところにも正規分布の裾野が伸びており、積分した値を適切に獲得関数とみなすことができません。
では、このような場合はどのように対処したらよいでしょうか。
y が原理的に0以下にならないときは、対数変換を使用するとよいでしょう。
対数変換をすることで、0 ~ ∞ の y が、−∞ ~ ∞ の変数に変換されます。y の目標値、例えば0.05 も対数変換し、−∞ から変換した値まで積分すれば、それを妥当な獲得関数として定義できます。
また y が 0 から 1 の範囲しか取らない場合にはロジット変換を使用します。
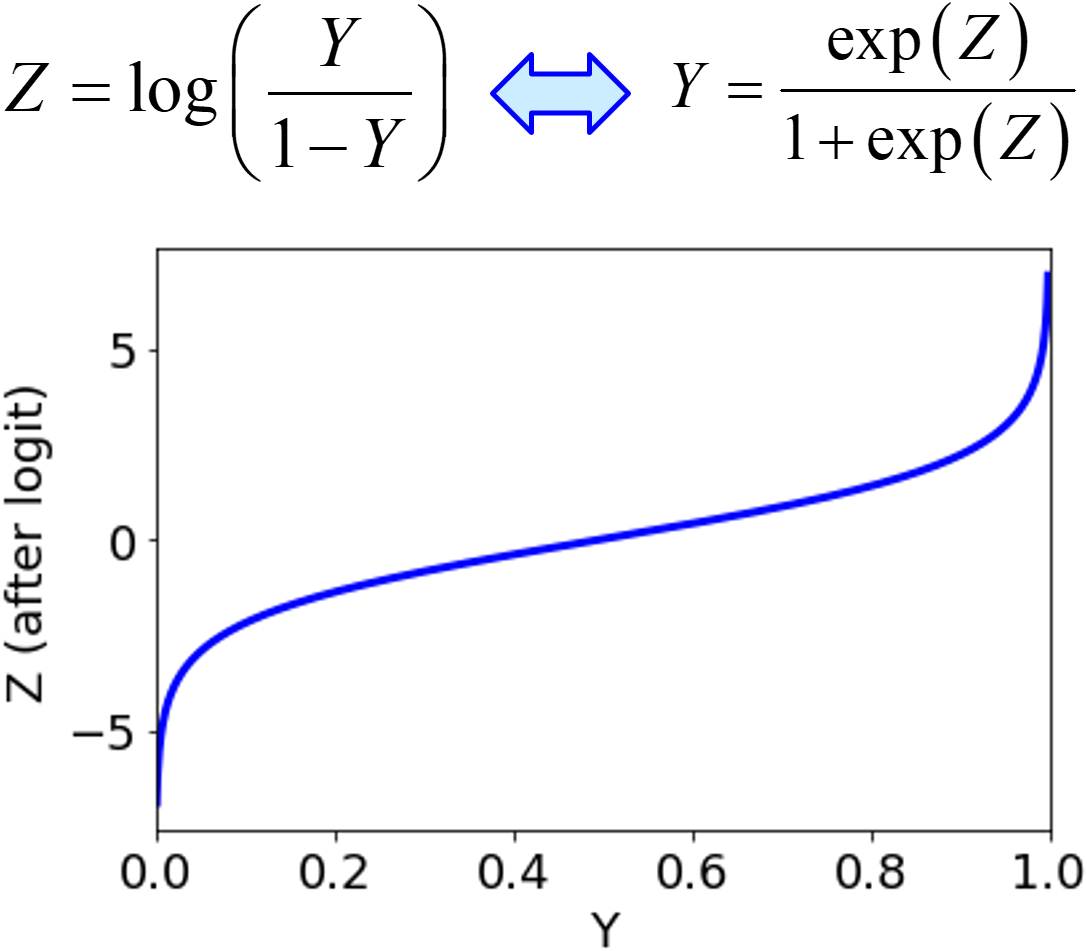
ロジット変換をすることで、0 から 1 までの y が、−∞ ~ ∞ の変数に変換されます。y の目標値についてもロジット変換し、−∞ から変換した値まで、もしくは変換した値から ∞ まで、積分すれば、それを妥当な獲得関数として定義できます。
このように、もともとの y に制限があるときは、適切な変数変換をすることで対処できます。今回は y が0 より大きい場合や 0 から 1 までの場合を例にしましたが、他の場合でもマイナスをかけて、適切な数値を足したり引いたり割ったりして、0 より大きい場合や 0 から 1 までの場合に変換してから、それぞれ対数変換、ロジット変換を適用できます。例えば 10 より小さい値しか取らない場合には、−1をかけて10 を足して 0 より大きい変数に変換した後に、対数変換します。3 から 20 の範囲しか取らない場合には、3 を引いてから 17 (=20 − 3) で割ることで 0 から 1 までの変数に変換した後に、ロジット変換します。参考になれば幸いです。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


